|
Benvenuto,
Ospite
|
ARGOMENTO:
Simmetrie: protoni, neutroni, … e quarks 09/07/2013 23:34 #80
|
Simmetrie: protoni, neutroni … e quarks
................
................
Per domande: autore o
Domanda a un esperto
................
Seguendo lo scorrere del tempo storico, si è partiti da considerazioni di simmetria per dedurre l'esistenza di costituenti elementari degli adroni (i " quarks "), come se l'esistenza degli atomi fosse stata dedotta dallo studio delle simmetrie dei cristalli minerali. Le simmetrie sono successivamente diventate lo strumento concettuale per descrivere e in certi casi predire la struttura degli adroni tramite il cosiddetto "Modello a quarks", introdotto in Interazione Forte e trattato in quest'articolo privilegiando gli aspetti riguardanti le simmetrie, che ne costituiscono il filo conduttore. Un approfondimento di carattere più avanzato è fornito in Simmetrie: quarks per semi-professionisti . La conferma del Modello fu fornita dall'osservazione di adroni predetti e precedentemente ignoti. Tenete presente che una simmetria è matematicamente definita da una "Invarianza" rispetto a una "trasformazione di coordinate - qualunque ne siano numero e natura. Si giunge a comprenderlo in Simmetrie: dai solidi platonici alla struttura cristallina , in un percorso nella Storia, nella Scienza e nell'Arte. Simmetrie e spazio astratto Si tende comunemente a pensare che l’aggettivo “astratto” si applichi a una “idea assurda, utopia”, come ammette anche il Grande Dizionario Italiano Gabrielli . Ma dovremmo essere ben coscienti di altri suoi significati, non solo nella Scienza per la quale l'astrazione è uno strumento fondamentale.
Per i cristalli minerali e la loro struttura, la simmetria va vista nello "spazio materiale" in cui sono distribuiti gli atomi che li costituiscono. Come vedremo nel seguito, per gli adroni la simmetria è cercata e studiata in uno "spazio astratto" in cui situiamo punti definiti da "numeri quantici" e individuati in base a simmetrie. Date le premesse storiche sopra appena evocate, perché dovremmo sorprenderci che si ragioni in uno spazio astratto? Riprenderemo il discorso nell'Appendice Fagioli, astrazione e Scienza. Adroni: barioni e mesoni La tabella in figura 3 mostra i primi elementi nella classificazione degli adroni agli inizi degli anni sessanta, all'epoca in cui si situa la storia che qui narriamo. Le particelle subnucleari costituenti il nucleo atomico – protone e neutrone – sono i capostipiti della classe detta dei “barioni” (dal greco βαρύς, pesante). Nel 1947 fu scoperto il “pione”, capostipite di una nuova classe che fu detta dei “mesoni” perché il pione ha massa intermedia tra quella dell’elettrone e quelle di protone e neutrone. A barioni e mesoni viene dato il nome generico di “ adroni ” (dal greco ἁδρός, forte), perché soggetti alla Interazione Forte . Per conoscere meglio gli adroni, vedete Protone, pione & adroni . 
Fig. 3. Adroni e loro classificazione Continuiamo la presentazione della tabella con qualche parola sulle vicende di vita delle particelle che vi compaiono. Neutrone e protone sono naturalmente presenti nei nuclei atomici della materia ordinaria. Nel quadro delle attuali conoscenze, il protone come particella isolata è del tutto stabile: non può scendere più in basso, non trovando un barione di massa inferiore in cui decadere. La massa del neutrone di pochissimo superiore a quella del protone permette un suo "decadimento β" in protone, ma con vita media (circa 15 minuti) enorme relativamente al mondo delle particelle elementari. Se desiderate approfondire vedete Interazione Elettro-Debole . Nella sua Appendice potete anche soddisfare la curiosità di capire perché parlando della stabilità del protone abbiamo specificato alla chetichella "come particella isolata". Le altre particelle in figura 3 - e in generale gli altri adroni - nascono in processi di collisione ad alta energia innescati naturalmente da raggi cosmici o artificialmente mediante acceleratori di particelle. Esse sono tutte instabili, con tempi di vita variabili ma generalmente molto piccoli. Per esempio, i pioni carichi hanno una vita media di circa 3 x 10-8 secondi (30 miliardesimi) e quello neutro di circa 8 x 10-17 secondi. La tabella comprende anche le cosiddette particelle " strane ", sulle quali torneremo in seguito. Esse hanno una massa più grande di quelle analoghe ma non dotate di "stranezza", e per di più sono instabili con tempi di decadimento molto lunghi rispetto a quelli attesi dai limiti l'interazione stessa addetta alla loro coesione: vedete Interazione Forte . Essi sono invece tipici dell'Interazione Debole, responsabile dei "decadimenti β" di nuclei atomici e caratterizzata dalla capacità di mutare l'identità delle particelle (vedete Interazione Elettro-Debole e Radioattività e decadimenti nucleari ). Masse e tempi di vita relativamente elevati indicano che le particelle strane sono "diverse". Il loro stesso nome di battesimo dice che esse escono dalla "normalità" di protone, neutrone e pione. Con la scoperta della stranezza, ai mesoni si aggiunsero i "mesoni strani" e in primo luogo i mesoni K. Ai barioni si aggiunsero gli "iperoni". Cicli storici anche nella Scienza Di fronte alla varietà degli elementi chimici, Dmitrij Mendeleev si era messo alla ricerca di "periodicità". La sua prima " Tavola Periodica " fu pubblicata nel 1869. Le periodicità prefigurarono la visione dell'atomo dato dalla Fisica Atomica, nella quale esse trovarono interpretazione (vedete Da Leucippo alla Fisica Atomica ). Qualcosa di simile avvenne per gli adroni. Al crescere del numero di adroni osservati, si cominciò a dubitare che essi fossero genuinamente particelle elementari e iniziò la ricerca di "simmetrie" (per uno sguardo d'insieme, vedete Dalla Fisica Nucleare al bosone di Higgs ). Simmetria di isospin Tra neutrone e protone emerge una prima simmetria. Essi hanno massa praticamente uguale, quella del neutrone essendo di pochissimo maggiore. La diversità che usualmente colpisce è nella carica elettrica. Ma questa ha un interesse secondario nel determinare il loro comportamento caratterizzante.
O come era per l'antica divinità italica " Giano Bifronte ": una intrigante divinità con lo stesso viso orientato in due direzioni opposte (figura 4). La stranezza estende nel campo delle simmetrie Parliamo di adroni osservati sperimentalmente e non consideriamo ancora la loro composizione in termini di quarks, né ragioniamo in termini di "stati quantistici" (vedete Onde e particelle per pedoni molto curiosi ) come è fatto sviluppando il Modello a quarks in Simmetrie: quarks per semi-professionisti . Come esempio consideriamo i barioni con spin J = ½ , tra i quali si trovano neutrone e protone. In base alla simmetria di isospin, come indicato in figura 5 neutrone e protone possono essere disposti simmetricamente rispetto all'origine di un asse orizzontale I3 . La simmetria di isospin - plausibile per quanto detto precedentemente - è quantitativamente rispettata anche nel paragonare le probabilità di processi fisici che coinvolgono neutrone e protone. Tuttavia, essa ha una portata limitata come strumento di simmetria per trarre indicazioni sulla struttura degli adroni: neutrone e protone potrebbero essere allineati simmetricamente rispetto a un punto centrale di riferimento anche introducendo un numero quantico artificiosamente ad hoc, senza dover necessariamente pensare a una sua origine strutturale. Per imporsi come inequivocabilmente non casuale, una simmetria deve rispettare un maggior numero di vincoli imposti da una corrispondenza con particelle osservate. La scoperta delle particelle strane (vedete Protone, pione & adroni ) con associato un numero quantico di "stranezza" S mise in campo un'altra varietà di particelle e offrì questa opportunità. La sua stessa denominazione fa intuire che la stranezza S esce dalla "normalità" dell'asse orizzontale I3 : in figura 5 è messa come asse verticale. Considerando anche quelli strani, emerge così l'indubbia simmetria di un "ottetto" di barioni con spin J = ½ , costituito da sei barioni situati ai vertici di un esagono e da due sovrapposti in corrispondenza del suo centro.
Arrivano i quarks Nelle storie delle famiglie vi sono anni con eventi importanti. Il 1964 lo fu per quella delle particelle elementari: Murray Gell-Mann (a 35 anni di età) e George Zweig (27 anni) indipendentemente "inventarono" i quarks come costituenti degli adroni per spiegare le simmetrie osservate. Essi hanno mantenuto la denominazione data da Gell-Mann, che pubblicò per primo ed ebbe Premio Nobel 1969 . Nacque così il “Modello a quarks" degli adroni, con i barioni costituiti di tre quarks e i mesoni di un quark e un antiquark. La figura 5 indica la composizione dei barioni con spin J = ½ situati ai vertici dell'esagono secondo il Modello a quarks. Il protone (uud) è costituito di due quarks denominati “up” (in breve u) e di uno “down” (d), e il neutrone (ddu) ha costituenti simmetrici per inversione del segno dell'isospin I3 dei quarks, ossia per scambio di up con down. I barioni strani contengono almeno un quark strano (s). La composizione dei due barioni sovrapposti al centro dell'esagono riveste un carattere più complesso, come delineato in Simmetrie: quarks per semi-professionisti . I quarks hanno spin ½ ed "eretiche" cariche frazionarie: -⅓ per down e strano, +⅔ per up). Ma eretiche apparivano solo perché l'elettrone si era da tempo accaparrato la carica considerata come unitaria. Fate i conti sommando le cariche dei quarks e ritroverete le cariche +1 del protone (uud) e 0 del neutrone (ddu), per esempio. Un ingrediente fondamentale del Modello a quark è che essi siano dotati un'ulteriore proprietà, secondo un'ipotesi scaturita da una precedente interpretazione di dati sperimentali. Essa è detta "colore". Il colore dei quarks è cosa totalmente diversa da quello della visione. La connessione - di natura logica - è esposta Viaggio nei colori: quarks e gluoni e più brevemente in Interazione Forte . Arrivano altri quarks: simmetrie nello spazio e nell'iper-spazio Oggi sappiamo che esistono sei tipi di quarks, disposti in tre "famiglie": "down" - "up", "strano" - "charm", “bottom” - “top” (in breve d - u, s - c, b - t), come mostrato in figura 6. Nel linguaggio della Fisica invece di “tipo”, parola troppo generica per non rischiare di creare confusione, si dice “sapore”. Anche nella nautica per evitare confusione si usa uno speciale gergo. I quarks hanno spin ½ come l’elettrone. La carica elettrica è -⅓ per il membro inferiore di ciascuna famiglia e +⅔ per quello superiore. Il Modello a quarks situa gli adroni ai vertici o in altri punti particolari di forme simmetriche astratte, definite in uno spazio multi-dimensionale i cui assi cartesiani sono definiti da specifiche proprietà di adroni e quarks, date da “numeri quantici di sapore” definiti nell'articolo di approfondimento Simmetrie: quarks per semi-professionisti . I numeri quantici di sapore degli adroni sono la somma di quelli dei quarks che li costituiscono. Le simmetrie si riferiscono alla disposizione dei singoli adroni in questo spazio astratto. Con i sapori dei 3 quarks scelti tra i 3 down, up e strano si ottiene una struttura simmetrica bidimensionale, come quella mostrata in Fig. 5 per i barioni con spin J = ½ . Con sapori dei 3 quarks scelti tra i 4 down, up, strano e charm se ne ottiene una tridimensionale. Le strutture simmetriche costituite da 3 quarks con sapori scelti tra 5 o tutti i 6 sapori sono collocate in un iper-spazio a quattro e rispettivamente cinque dimensioni. Tali iper-strutture sono rappresentabili solo matematicamente.
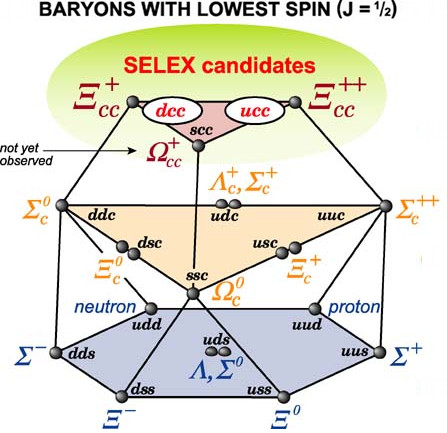
Barioni con spin totale J = ½ Per dare un esempio concreto, mostriamo in figura 7 la struttura simmetrica corrispondente ai barioni con spin J = ½ e costituiti da 3 quarks con sapori scelti tra i 4 up, down, strano e charm. Rispetto al caso di figura 5, l'aggiunta di un quarto quark aggiunge una terza dimensione posta secondo un asse verticale in cui viene messo il numero quantico di charm. La simmetria che vediamo in figura 7 è più complessa di quella dei poliedri regolari come i "solidi platonici" (vedete Simmetrie: dai solidi platonici alla struttura cristallina ), ma ben visibile. La sua forma geometrica in tre dimensioni ha facce di forma regolare ma diverse. Sui lati della faccia esagonale di base (la stessa di figura 5) si saldano tre facce esagonali inclinate, a cui si alternano facce triangolari che colmano i vuoti lasciati da esse. Come nel caso di figura 5, i barioni situati ai vertici delle facce esagonali hanno due dei tre quarks uguali (come protone e neutrone). I barioni centrali hanno quarks tutti diversi tra loro. Con la figura 8, Leonardo da Vinci (1452-1519) ci aiuta a vedere la struttura simmetrica in figura 7. Essa rappresenta un " tetraedro troncato " cioè un tetraedro con le cuspidi tagliate. In Geometria, esso è uno dei 13 " solidi archimedei ", solidi regolari che si aggiungono ai solidi platonici rimuovendo la condizione che le facce siano tutte uguali. Notiamo che a rigore il Modello a quarks definisce strutture simmetriche costituite da "stati quantistici", come esposto in Simmetrie: quarks per semi-professionisti assieme alla loro relazione con gli adroni. Conferme sperimentali Si poee una domanda d’obbligo: il Modello a quarks corrisponde veramente alla realtà fisica? Riprodurre quanto è noto non basta, potrebbe essere un artificio. In una struttura simmetrica formata da quarks, ogni adrone ha il suo posto e se un posto è vuoto deve esistere un adrone non ancora osservato che lo occupi. Come per ogni teoria, la risposta inequivocabile viene da una esauriente verifica del suo potere predittivo, dalla capacità di fare un salto nel buio e di trovarvi quanto predetto dalla teoria. La prova della validità del Modello a quarks venne appunto dalla verifica del suo potere predittivo tramite la scoperta di adroni che occupano i posti vuoti. Questo tipo di ricerca continua per adroni con caratteristiche speciali, “esotici”, predetti dal Modello a Quarks. Lo vedete in figura 7, tratta dal sito Web di un recente esperimento per la ricerca di barioni con doppio charm e carica elettrica +2. Una fondamentale conferma della loro esistenza fu data sondando la struttura del protone e del neutrone in esperimenti "alla Rutherford". Utilizzando come sonde elettroni ad altissima energia, venne evidenziata l'esistenza di loro costituenti "puntiformi" con le proprietà dei quarks. Fu così anche dimostrato che essi possono essere considerati particelle elementari "indivisibili" secondo la concezione di Leucippo e Democrito, al pari dell'elettrone (vedete Interazione Forte e Da Leucippo alla Fisica Atomica ).
Al pari della teoria dell'Interazione Elettro-Debole (vedete Interazione Elettro-Debole ), la QCD deriva da una impostazione sostanzialmente teorica basata uno dei più importanti progressi del sapere in questi ultimi decenni: la magica relazione tra Simmetrie e Interazioni Fondamentali. Di questo trattano Simmetrie e Interazioni Fondamentali e Interazione Forte . E per finire: domande La simmetrie hanno portato alla luce l'esistenza dei quarks e prodotto il Modello a quarks, che descrive correttamente e senza ambiguità le proprietà degli adroni. La parola quark è entrata nel linguaggio corrente, dove è usata per attrarre l’attenzione anche di persone che sostanzialmente non sanno che cosa significa.
APPENDICE
Il
Grande Dizionario Italiano Gabrielli
dice anche che l’astrazione è una “operazione mentale che tende a separare le qualità essenziali di un oggetto, prescindendo da quelle accidentali, per ricavarne il concetto universale”. In tale accezione, l’aggettivo “astratto” denota una superiore entità universale, e non qualcosa di disconnesso dalla realtà.Fagioli, astrazione e Scienza ...... Pratichiamo l'astrazione nella vita di tutti i giorni, anche senza accorgercene. Lo è da tempi remoti la “ numerazione ” con una base, che essa sia 2, 10 o altro. Senza di essa saremmo ancora al punto di contare mettendo di volta in volta un fagiolo in un mucchio, come il personaggio in figura A1. E’ il "bean counting" (“conteggio con fagioli”) di cui parla Feynman nel libro QED, la strana teoria della luce e della materia . Con i numeri si può far di conto molto più rapidamente che usando fagioli. La numerazione e le operazioni numeriche hanno cambiato la vita dell’uomo e per un intelletto logico 2 x 2 = 4 è altrettanto concreto che prendere 2 volte 2 fagioli.
L’intelletto umano è capace di concepire altre astrazioni, solide come 2 x 2 = 4 anche se più complesse. Lo sono la Geometria (figura A2) e la Matematica, che sviluppano a livello universale le loro metodologie con la potenza della logica astratta per utilizzarle nelle più svariate applicazioni. La Scienza ha fatto dell’astrazione uno strumento fondamentale. Per fare con un'analogia, gli aerei operano in modo analogo all'astrazione nella Scienza: decollano dal suolo, volano ad alta quota con i loro strumenti e atterrando sono di nuovo sul suolo. E ci portano rapidamente più lontano di quanto non possano le nostre sole gambe. In particolare, i quarks sono nati da una sintesi di dati sperimentali utilizzando i metodi matematici propri delle simmetrie. Anche il tetraedro troncato di figura 8, definito dalla Geometria dell’antica Grecia e disegnato da Leonardo da Vinci, è nella linea scientifica che ha portato alla scoperta dei quarks e alla comprensione della struttura degli adroni.
Paolo Strolin
. Professore Emerito di Fisica Sperimentale
Università di Napoli "Federico II" Complesso Univ. Monte S. Angelo Via Cintia - 80126 Napoli - Italy |
|||||||||||||||||||||||
|
Si prega Accedi a partecipare alla conversazione. |
Tempo creazione pagina: 0.606 secondi