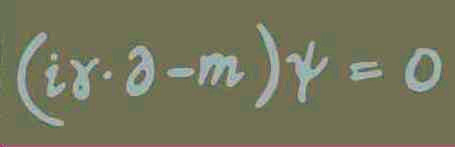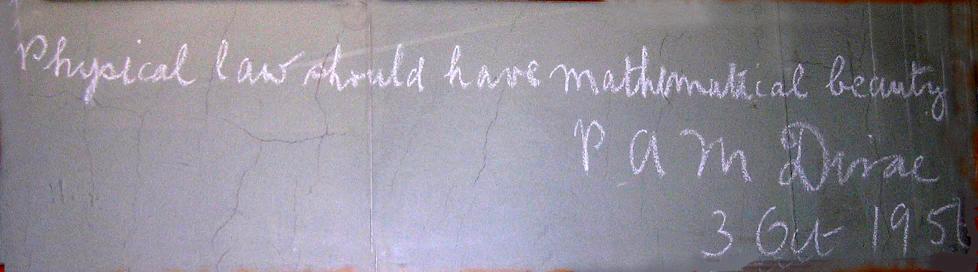Interazioni "Alla Feynman"
- P. Strolin
-
Autore della discussione
- Offline
- Premium Utente
-
Less
Di più
12 Anni 11 Mesi fa - 9 Anni 1 Mese fa #66
da P. Strolin
Quali “icone” inserire come “ouverture” a una visione della “Interazione Elettromagnetica”? Le leggi dell’elettromagnetismo classico in quattro righe: questo potremmo scrivere come didascalia di figura 1, dedicata alle “Equazioni di Maxwell”. Iniziando questo nostro percorso con il parlare della formulazione dell'Interazione elettrostatica (1785), vedremo che nel 1864 esse costituirono un grandioso e sinteticamente semplice coronamento a secoli di riflessioni e di studi sui fenomeni elettrici e magnetici nell’ambito cosiddetta “fisica classica”, per intendersi quella che era la Fisica prima della rivoluzione scientifica avvenuta nei primi decenni del Novecento. E vedremo che inquadrando teoricamente le “onde elettromagnetiche” (situandovi nientemeno che la luce) esse andarono molto oltre sia dal punto di vista teorico che da quello delle applicazioni pratiche.
La seconda icona può ben riguardare Richard Feynman (1918-88) e i suoi “diagrammi”. Essa è mostrata in figura 2. I diagrammi di Feynman completarono gli studi che portarono all’attuale teoria quantistica-relativistica dell’Interazione Elettromagnetica (la cosiddetta Elettro-Dinamica Quantistica, in breve QED) con un nuovo modo grafico-matematico di formulare un processo fisico, al tempo stesso rigoroso e visivamente comprensibile nel rappresentare la sua essenza. Incontreremo queste pietre miliari sulla strada che percorreremo, quella dell'Interazione Elettromagnetica, facendo tappa ove parrà particolarmente significativo.
Quest'articolo è complementare a L'enigma dell'interazione a distanza e i "quanti" e affronta l'argomento privilegiando gli aspetti concettuali e la loro storia. A essi segue Il Vuoto quantistico .
Interazione elettrostatica
La ben nota legge di Coulomb definisce quantitativamente le “forze” uguali e opposte che agiscono su due corpi elettricamente carichi in condizioni statiche, per "interazione" elettrostatica". Sottolineiamo la distinzione lessicale e sostanziale tra forza e interazione: la forza agisce su un singolo corpo, l'interazione indica il fenomeno globale che determina la trasmissione di forze ai corpi coinvolti.
La figura 3 mostra una raffinatissima “ bilancia a torsione ”, simile a quella utilizzata nel 1785 (pochi anni prima della Rivoluzione) dal nobile francese Charles Augustin de Coulomb (1736-1806) per stabilire la legge omonima della forza elettrostatica. Notate in figura 4 lo strumento usato dallo scienziato, in un dipinto che raffigura lo stesso de Coulomb. La torsione del filo costituisce la molla di un sensibilissimo dinamometro e la forza di gravità è ingegnosamente compensata tramite un bilanciere. Una bella e completa descrizione della misura è fornita nel collegamento ipertestuale fornito sopra.
Negli anni 1797-98 dello stesso periodo storico, la tecnica della bilancia a torsione fu usata anche da Henry Cavendish (1731-1810) per misurare in laboratorio la Costante di Gravitazione Universale G, fino ad allora "dedotta" dall'osservazione di fenomeni su scala terrestre o del sistema solare. Questa misura permise anche “ pesare la Terra ”: il valore della massa M della Terra fu dedotto inserendo il valore di G nell’espressione g = G M / R 2 dell'accelerazione di gravità g - individuata e misurata da Galileo (1564-1642) - ove R è il raggio della Terra. A questo proposito, non si può non ricordare la sempre sorprendente misura di R nel III secolo a.C. da parte di Eratostene . Per maggiori dettagli sulla bilancia a torsione e sulla misura di Cavendish, vedete Interazione Gravitazionale .
Perché si parla di “campi”?
Una volta appreso, l’uso di un linguaggio parlato semplifica la vita rispetto a quello dei gesti. Vale la pena apprendere anche i linguaggi della Scienza, impegnandosi e graduando l’approfondimento secondo la necessità. Una parola del linguaggio della Fisica è "campo". Il concetto di campo costituisce un’ astrazione molto generale. Come esempio, vediamone l’utilità per l’elettromagnetismo classico.
Se posta a una certa distanza da una carica elettrica Q, una carica q subisce una certa forza F e . Se la carica q raddoppia, la forza raddoppia. Quello che non cambia è il rapporto E = F e / q, ossia la forza per unità di carica: ecco nato naturalmente il campo elettrico E, che può essere definito in tutto lo spazio indipendentemente dalla carica q e in funzione unicamente dalla sua sorgente Q: la “astrazione fisica” E è più generale della forza F e .
La forza magnetica F m è detta " Forza di Lorentz ” e dipende non solo dalla carica q, ma anche dalla velocità v del corpo su cui essa si esercita. Anche per essa vale una generalizzazione in termini di un campo magnetico B, secondo la relazione F m = q v B. Il campo magnetico dipende unicamente da una sua sorgente, che però è una corrente e non una carica elettrica. Le leggi sono ben note e (nelle loro formulazioni più semplici) sono riportate praticamente in qualsiasi testo.
La forza elettrica e il relativo campo hanno la stessa direzione. Nella relazione tra forza magnetica e campo magnetico si inserisce anche la velocità, essa stessa caratterizzata da una direzione e da un verso: sono tutti "vettori". Il prodotto v B è un " prodotto vettoriale " e il suo risultato è una forza magnetica perpendicolare ad ambedue i fattori, con verso dato dalla cosiddetta "regola della mano destra".
Equazioni di Maxwell
Le equazioni di Maxwell legano il campo elettrico e quello magnetico a sorgenti costituite da cariche e correnti elettriche, in un quadro globale. Esse sono riportate in figura 1, in una formulazione che implica derivate e in cui appare un campo D, ma è collegato al campo elettrico E. Con la loro formulazione, all’età di 33 anni (ma perché lo si raffigura sempre anziano?) James Clerk Maxwell (1831-79) nel 1864 portò a compimento un processo di comprensione rigorosamente scientifica della connessione tra fenomeni elettrici e magnetici, iniziato con l'osservazione di Hans Christian Oersted (1777-1851) che una corrente elettrica genera un campo magnetico.
Maxwell operò una vera e propria “unificazione” di interazioni (elettrica e magnetica), sulla strada aperta nel 1687 dalla "Gravitazione Universale" di Isaac Newton (vedete Interazione Gravitazionale ). Così da un secolo e mezzo siamo abituati a parlare di elettro-magnetismo, unificando nell’ambito della fisica classica la descrizione dei fenomeni elettrici e magnetici in un struttura teorica comune, data appunto dalle Equazioni di Maxwell. Vedremo poi cosa significa unificazione per la fisica moderna, nell’ambito quantistico-relativistico.
Per situare l'opera di Maxwell nello svolgersi della Storia dell’umanità senza limitarsi ai suoi aspetti scientifici, ricordiamo che Thomas Alva Edison (1847-1831) inventò la lampadina a incandescenza nel 1878 e che questa tecnologia permise di realizzare il primo impianto di illuminazione pubblica tramite elettricità a New York nel 1882.
Ricordiamo altresì che il motore elettrico cosiddetto “ asincrono ”, di importanza decisiva per il suo sviluppo, fu inventato nel 1885 da Galileo Ferraris (1847-97). Secondo il noto vizio italiano egli non lo brevettò. L’industria americana Westinghouse ebbe mani libere e nel 1892 realizzò il primo motore elettrico commerciale.
Le Equazioni di Maxwell (1864) sono antecedenti ai suddetti sviluppi tecnologici ed essi stessi sono basati su leggi individuate ancora prima. Le Equazioni di Maxwell portano ben oltre sia dal punto di vista della conoscenza che da quello di applicazioni pratiche rilevanti per l'umanità, come vedremo. La Scienza precorre i tempi e apre strade che portano a tecnologie impensate.
Equazioni di Maxwell, luce e Teoria della Relatività Speciale
Le leggi dell’elettromagnetismo, disgiunte prima di Maxwell, erano bastate per l’invenzione delle macchine elettriche. Ma vi era un’asimmetria: un campo magnetico variabile “induceva” un campo elettrico, ma vi era silenzio sul contrario. Maxwell le considerò tutte assieme in un “sistema di equazioni” e con la forza del ragionamento le simmetrizzò introducendo ∂D/∂t nel secondo membro della quarta equazione in figura 1 e simmetrizzando così ∂B/∂t nella terza equazione (per ci volesse approfondire, D è una grandezza collegata al campo elettrico E e i simboli ∂ si riferiscono a operazioni matematiche dette "derivate").
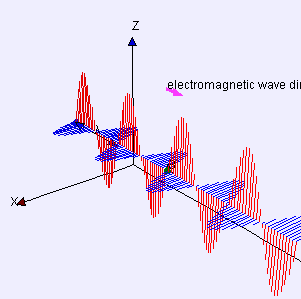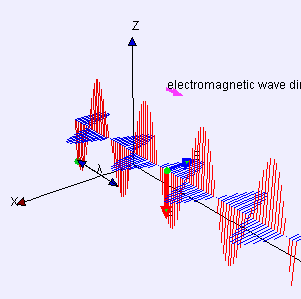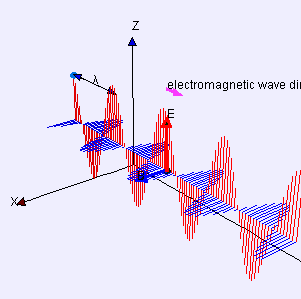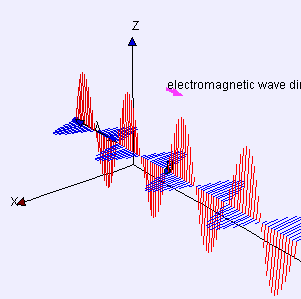
Al ruolo simmetrico dei campi elettrico e magnetico nelle Equazioni di Maxwell consegue l’esistenza di “onde elettromagnetiche”. Un’onda elettromagnetica è un "campo elettromagnetico" che si propaga e consiste in un campo elettrico E e uno magnetico B oscillanti trasversalmente alla sua direzione di propagazione e perpendicolarmente tra loro. La figura 5 mostra un'onda "polarizzata linearmente", nella quale i campi elettrico e magnetico non mutano direzione di oscillazione.
L’esistenza delle onde elettromagnetiche predette da Maxwell fu dimostrata sperimentalmente nel 1885 da Heinrich Rudolf Hertz (1857-94), che riuscì a produrle in laboratorio e a osservarle. Ora sappiamo che le onde elettromagnetiche coprono un larghissimo spettro di frequenze , che corre da quelle delle onde radio a quelle della cosiddetta “radiazione γ”.
Nel vuoto, le onde elettromagnetiche predette dalle Equazioni di Maxwell si propagano con la velocità della luce. Esse avvalorarono l’ipotesi della natura ondulatoria della luce, basata sull’ osservazione di fenomeni diffrattivi .
L’indipendenza della velocità della luce dal sistema di riferimento nelle Equazioni di Maxwell, confermata dall’esperimento di Michelson-Morley (1887), fu poi all’origine della Teoria della Relatività Speciale formulata da Albert Einstein nel 1905: vedete Simmetrie e Relatività Speciale .
La vastità delle applicazioni pratiche delle onde elettromagnetiche è enorme. Come esempio, la figura 6 mostra il Carpathia in soccorso dei naufraghi del Titanic in seguito al primo SOS via onde radio nella storia, dato nel 1912 con un radiotelegrafo installato sul Titanic dall'inventore della trasmissione via onde radio: Guglielmo Marconi (1874-1937).
Equazioni di campo per onde e particelle
La denominazione stessa lo dice, parzialmente: le Equazioni di Maxwell hanno segnato la transizione da una descrizione di fenomeni specifici in termini di “leggi” a una di valenza più ampia in termini di “Equazioni di campo”, con profilo sostanzialmente autonomo. Tuttavia, ai tempi di Maxwell, campi e oggetti sui quali essi si esercitano (particelle elementari nella fisica di oggi) erano cose ben distinte.
Nel secolo successivo, il ‘900 si sviluppò la fisica quantistica (vedete Da linee di Fraunhofer ad atomo quantistico e Onde e particelle per pedoni molto curiosi ). In particolare, i’ ipotesi di de Broglie (1924) sulla natura anche ondulatoria dell’elettrone cancellò il confine tra onde e particelle. La descrizione di ambedue in termini di campi aprì la strada per la loro coesistenza in una stessa equazione di campo, capace di descrivere le interazioni tra particelle. Lo vedremo per quella elettromagnetica.
Equazioni di campo: onde e mediatori
Nella classica interazione a distanza, il campo generato da una sorgente si stabilisce simultaneamente ovunque. La scoperta di Maxwell che il campo elettromagnetico si propaga come un'onda fu il preludio della sua fine: l'interazione è trasmessa da un'onda ed essa ha velocità finita. L'equivalenza quantistica onda-particella portò infine al concetto di “mediatore” di una interazione, cioè di una particella che la trasmette.
Dai tempi di Newton che la introdusse, l'interazione a distanza regge ancora per l'Interazione Gravitazionale, non essendovi tuttora una sua teoria quantistica. Per migliore conoscenza, vedete L'enigma dell'interazione a distanza e i "quanti" .
Interazione Elettromagnetica: formulazione quantistica
In fisica classica, il campo elettromagnetico abita nelle Equazioni di Maxwell assieme a cariche e correnti elettriche. Nella formulazione quantistica cariche e correnti sono sostituite da particelle in moto, il cui comportamento è descritto da campi tramite un'equazione quantistica-ondulatoria. Per l’Interazione Elettromagnetica, il campo elettromagnetico viene opportunamente inserito nell’equazione che descrive le particelle. Il mediatore lo traduce quantisticamente e corrisponde alla particella detta “ fotone ”.
Questo vale in particolare per l’elettrone, archetipo di particella elementare e in generale preso come riferimento. Inizialmente l'elettrone libero fu descritto tramite l’ equazione di Schrödinger (1926), limitata tuttavia a un dominio non-relativistico: andremo direttamente oltre.
Nel 1927 la famosa Equazione di Dirac fornì la prima rappresentazione relativistica del comportamento dell’elettrone, valida anche per altre particelle elementari. Essa fu concepita per superare la limitazione a energie non-relativistiche dell'equazione di Schrödinger, ma la prodigiosa intuizione di Dirac nel concepirla portò ulteriori e sorprendenti frutti.
La prima sorpresa fu l’automatica e inattesa inclusione nell’equazione stessa di una tuttora inspiegabile ma reale proprietà dell’elettrone: il suo “momento angolare di spin” (vedete Lo spin e altri sull'argomento tra i Saggi tematici ), assente nell’Equazione di Schrödinger. L’Equazione di Dirac fornì inoltre la rivoluzionaria predizione dell’esistenza di anti-particelle . La predizione di Dirac trovò conferma nel 1932 con la scoperta dell’anti-elettrone, comunemente detto “ positrone ”.
Paul Dirac fu insignito del Premio Nobel 1933 per la Fisica, assieme a Erwin Schrödinger . L'Equazione di Dirac è mostrata in figura 7a: come da sempre, l'invenzione di nuovi formalismi matematici rende semplice la rappresentazione di questioni complesse. L'Equazione di Dirac ha anche "bellezza matematica", in accordo con l'affermazione generale nel manoscritto di Dirac sulla lavagna in figura 7b.
Sulla base dell’Equazione di Dirac, gli anni ’40-’50 videro lo sviluppo della “ Elettro-Dinamica Quantistica ” (QED) e della descrizione grafica-matematica dei processi fisici tramite i diagrammi di Feynman . La QED fornisce una metodologia di calcolo che estende alle alte energie il dominio di applicazione della descrizione quantistica-relativistica dei processi elettromagnetici e porta a una straordinaria precisione la descrizione dei processi a bassa energia. Quanto ai diagrammi di Feynman, essi sono nati con la QED ma come metodo hanno un'applicabilità molto più generale.
Perle e sistemi quantistici
La pesatrice di perle (o donna che pesa dell’oro) nel dipinto di Jan Vermeer (1632-76) in figura 8 procede per approssimazioni successive, stimando di volta il pesetto da aggiungere o togliere per una pesata con la precisione desiderata.
Fig. 8. Jan Vermeer, La pesatrice di perle (dettaglio, 1662-5), National Gallery of Art, Washington - Immagine Millequadri
In fisica classica, tutto è in linea di principio rigorosamente e presuntuosamente calcolabile. A meno che non si entri in fenomeni caotici (come la turbolenza di un fluido, vedete Ali e vele ), che la apparentano a fenomeni sociali di insiemi di umani o animali (vedete La Scienza della Complessità ). Il ricorso alle approssimazioni successive è raro.
I sistemi quantistici hanno come “peccato originale” il Principio di Indeterminazione , dicendo peccato ma sempre restando il dubbio che l’imperfezione del peccato possa essere una forma di umanizzazione. I sistemi quantistici che si possono risolvere completamente sono molto pochi (uno di essi è l’atomo di Idrogeno, con un solo elettrone). Contrariamente al caso della fisica classica, nella maggior parte dei casi è quindi necessario procedere per approssimazioni successive. In particolare, si ricorre a una tecnica di calcolo che considera il fenomeno come una (piccola) perturbazione del quieto vivere del sistema, applicando il cosiddetto “ metodo perturbativo ”. La soluzione è quindi fornita per approssimazioni successive come per la pesatrice di perle, ma rigorosamente calcolate fino a raggiungere grandissime precisioni e non solo stimate.
Anche la QED è basata sul metodo perturbativo. Le predizioni sullo svolgersi di un processo fisico sono fornite sotto forma di “serie”, ossia di somme (secondo le regole quantistiche) di termini sempre più piccoli. I “diagrammi di Feynman” li rappresentano in forma grafica-matematica, ove il trattino ha lo stesso significato di quando lo vedete scritto per esempio in Vocabolario italiano-inglese. Il vocabolario per la traduzione sono le “regole di Feynman”.
Ci stiamo riferendo all’Interazione Elettro-Magnetica, ma la metodologia generale è applicabile anche nella trattazione quantistica di processi attribuibili ad altre interazioni Con opportuni accorgimenti, essa è applicabile sia a processi che avvengono in collisioni tra particelle che in processi di decadimento naturale di una particella, quale per esempio il decadimento β di un quark descritto in Interazione Elettro-Debole
In particolare, per esporre la metodologia ci riferiremo all'interazione tra due elettroni (A e che si muovono uno verso l’altro. Guardate i “disegni” schematici nel francobollo celebrativo in figura 2, e in particolare quello in basso al centro. Riportiamolo in figura 9 scrivendo A a sinistra e B a destra. Così, il disegno descrive proprio gli elettroni A e B in incontro ravvicinato. Vedremo che la linea ondulata che li collega rappresenta il fotone mediatore e che la figura 9 è molto di più di un "disegno": è un “diagramma di Feynman” e fornisce quantitativamente la "ampiezza di probabilità" (definita in
Onde e particelle per pedoni molto curiosi
) del processo, per quanto detto sopra a un primo livello di approssimazione.
che si muovono uno verso l’altro. Guardate i “disegni” schematici nel francobollo celebrativo in figura 2, e in particolare quello in basso al centro. Riportiamolo in figura 9 scrivendo A a sinistra e B a destra. Così, il disegno descrive proprio gli elettroni A e B in incontro ravvicinato. Vedremo che la linea ondulata che li collega rappresenta il fotone mediatore e che la figura 9 è molto di più di un "disegno": è un “diagramma di Feynman” e fornisce quantitativamente la "ampiezza di probabilità" (definita in
Onde e particelle per pedoni molto curiosi
) del processo, per quanto detto sopra a un primo livello di approssimazione.
Emissione e assorbimento di un fotone e costante di accoppiamento
Nell’interazione elettrostatica come vista da de Coulomb, l’elettrone A genera simultaneamente e dappertutto un astratto campo elettrico al quale è soggetto l’elettrone B, e viceversa. Come si è detto sopra, ora sappiamo che l’interazione è trasmessa da un campo elettromagnetico ondulatorio che si propaga a velocità finita (quella della luce) e in “quanti” (una sorta di pacchetti d’onda) detti "fotoni": si deve ragionare in termini di fotoni emessi e assorbiti dagli elettroni con una certa ampiezza di probabilità.
L’ampiezza di probabilità di emissione o assorbimento del fotone è data dalla cosiddetta “costante di accoppiamento”. Guardando la figura 9 se ne capisce la denominazione: essa corrisponde al vertice in cui fotone e elettrone si collegano, o accoppiano. Come esposto in Interazioni e loro unificazione , la costante di accoppiamento è l'etichetta che definisce il tipo d’interazione: stessa costante di accoppiamento, stessa interazione. La costante di accoppiamento dell’Interazione Elettro-Magnetica è data dalla carica "e" dell’elettrone, nello speciale sistema di unità di misura comunemente usato per le particelle elementari. Notate che dicendo “elettro-magnetica” abbiamo implicitamente assunto che interazioni elettriche e magnetiche siano unificate e caratterizzate dalla stessa costante di accoppiamento: in linguaggio non quantistico lo avevano già detto le Equazioni di Maxwell.
Diagrammi di Feynman
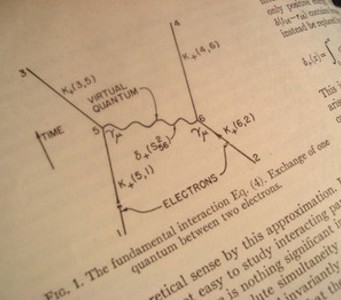
Come detto sopra, in realtà la figura 9 è molto di più di una raffigurazione visiva di processo fisico: ne è anche una sua rappresentazione quantitativa, al pari di un’espressione matematica, è un “diagramma di Feynman”. La figura 10 mostra il primo diagramma di Feynman, riprodotto dalla sua pubblicazione originale del 1949. Da allora, essi sono diventati strumenti basilari per studi e calcoli. Nella figura, ad ogni elemento grafico (segmento di linea o vertice) del diagramma è associata la sua "traduzione" in uno dei fattori che compaiono nella espressione matematica dell'ampiezza di probabilità che il processo avvenga (indicata come “Eq. (4)” nella didascalia originale nel lavoro di Feynman, visibile in figura). Il diagramma diventa così una scrittura in lingua grafica invece che nella usuale lingua matematica, con vantaggio di immediatezza di espressione e quindi di facilità di comprensione dell'essenza fisica del processo. Vediamo meglio come questo "funziona", almeno qualitativamente.
Iniziamo con i vertici. Abbiamo visto che con una certa ampiezza di probabilità l'elettrone A può "emettere" un fotone: questa ampiezza costituisce il fattore matematico associato al vertice di emissione del fotone. Un analogo fattore matematico viene associato al vertice in cui il fotone emesso è "assorbito" dall'elettrone B.
La trasmissione (o “propagazione”) del fotone da un vertice all'alto implica una sua propria ampiezza di probabilità, determinabile dalla fomulazione matematica del suo comportamento fisico: questa ampiezza costituisce il fattore matematico associato al segmento di linea ondulata, che nel diagramma di Feyman rappresenta il fotone. Il fotone trasmesso è detto “virtuale”, in relazione al fatto che esso nasce e muore all’interno del processo e non mette piede nel mondo esterno: anche se volessimo mettere delle frecce a indicare il verso in cui si muove, non sapremmo come metterle. Questa osservazione è espressione del fatto che il processo inverso (emissione del fotone da B e assorbimento da A) è inglobato nel diagramma. Questo spiega anche l’assenza di frecce nelle figure 9 e 10, che starebbero a indicare un verso per la propagazione del fotone.
L'ampiezza di probabilità complessiva per il processo è data dal prodotto dei suddetti tre fattori (emissione-propagazione-assorbimento), e di altri fattori matematici associati ai segmenti di linea che nel diagramma rappresentano le particelle che interagiscono nel processo. Analogamente al caso del fotone, questi fattori sono determinabili dalla fomulazione matematica del loro comportamento fisico. La "probabilità" complessiva è data dal quadrato della suddetta "ampiezza di probabilità" (vedete ad esempio " Onde e particelle per pedoni molto curiosi " su questo Forum).
In pratica, le regole di corrispondenza sono state determinate una volta per tutte e costituiscono le cosiddette "Regole di Feynman", che fortunatamente stanno approssimativamente in una pagina. Per qualsiasi processo, si può quindi convenientemente partire dalla sua rapprentazione in termini di diagrammi di Feyman (con i vantaggi di immediatezza detti sopra) e quindi utilizzare le Regole di Feynman come un dizionario per tradurne gli elementi (segmento, linea ondulata o vertice) fattori matematici.
La traduzione degli elementi grafici dei diagrammi di Feynman in fattori matematici ricorda (si intende solo in linea di principio) quella della scrittura simbolica dell’antico Egitto – i geroglifici – in una scrittura fonetica. La chiave per scoprire come farlo fu fornita dalla famosa Stele di Rosetta , mostrata in figura 11: è una splendida pietra nera e incisa, un'opera di arte antica da museo di arte moderna anche nel suo stato attuale di frammento. Se la sua storia vi incuriosisce, leggete l’Appendice dal titolo I geroglifici e la Stele di Rosetta.
Come si è detto, il diagramma in figura 9 rappresenta la prima approssimazione dell'ampiezza di probabilità complessiva. Le approssimazioni successive implicano ulteriori processi di emissione e assorbimento e quindi ulteriori fattori dati dalla costante di accoppiamento. Grazie al valore relativamente piccolo della costante di accoppiamento elettro-magnetica, già la prima approssimazione si avvicina alla probabilità complessiva con una precisione dell’ordine dell’uno per cento, che in moltissimi casi è sufficiente.
Per una introduzione qualitativa ai diagrammi di Feynman, vedete Da linee di Fraunhofer ad atomo quantistico . Per approfondimenti sugli ordini di approssimazione seguenti, vedete Il Vuoto quantistico .
Verifiche sperimentali
Per verificare la QED con la massima accuratezza, si è innescata una gara – tuttora in corso - tra fisici teorici e sperimentali: i teorici introducendo successivi livelli di approssimazione, gli sperimentali conducendo esperimenti sempre più raffinati e precisi. Si é così giunti a verificare la QED con la strabiliante accuratezza di 10 parti per miliardo !
Come già notato, a fine Settecento la legge di Coulomb era la conoscenza di frontiera corrispondente alla QED. La precisione della misura, e inizialmente anche la giustificazione sperimentale delle conclusioni tratte, fu controversa ed è tuttora oggetto di dibattito nell’ambito della Storia della Scienza. Essa fu comunque straordinaria per i mezzi di allora. Paragonate un suo valore indicativo, dell’ordine del 5%, alle 10 parti per miliardo raggiunte nella verifica della QED. Ogni commento sul progresso effettuato è superfluo.
Il discorso continua in …
Leggete Interazione Elettro-Debole e Simmetrie e interazioni fondamentali . Troverete che l’Interazione Elettromagnetica e la cosiddetta Debole sono ora unificate nella “Interazione Elettro-Debole”. Troverete inoltre che si può ribaltare la genesi della QED: da teoria sviluppatasi in base a una storia di osservazioni sperimentali, essa può essere formulata “a tavolino” imponendo una opportuna simmetria.
Collegamenti e riferimenti bibliografici
Richard P. Feynman, QED: the strange theory of light and matter - QED: la strana teoria della luce e della materia , Editore Princeton University Press (1965) - Adelphi (1989)
Appendice: I geroglifici e la Stele di Rosetta
I diagrammi di Feynman usano un linguaggio grafico simbolico traducibile in un’espressione matematica. Abbiamo caratteri grafici simbolici anche per le lingue scritte: abitualmente usiamo degli astratti caratteri fonetici, ma in lingue orientali si usano ideogrammi e nell’antico Egitto si usavano geroglifici .
Per secoli l’interpretazione e la traduzione dei geroglifici ha affascinato e impegnato gli studiosi. Citiamo in particolare il grande umanista e scienziato Athanasius Kircher (1602-80), di poco posteriore a Galileo. Nel linguaggio scientifico di oggi possiamo dire che ancora mancavano "dati sperimentali" che fornissero una chiave interpretativa e permettessero di andare oltre una metodologia essenzialmente speculativa.
La chiave decisiva per l’interpretazione dei geroglifici fu offerta dal ritrovamento nel 1799 della Stele di Rosetta (figura 11) nel corso della campagna napoleonica d’Egitto (1798-1801), al cui seguito vi era un folto stuolo studiosi. Il fascino dell'antico Egitto era grande anche per Napoleone Bonaparte, come simbolicamente mostrato nella suggestiva figura 12. Il rovescio della medaglia fu la spoliazione di numerosi capolavori. La stele - consegnata agli inglesi dopo la disfatta francese ad Abukir e ora al British Museum - riporta un decreto tolemaico del secondo secolo a.C. scritto in tre differenti grafie: egizia geroglifica, egizia demotica e greca.
Nel 1814 il grande scienziato Thomas Young per primo intuì che un cartiglio nel testo geroglifico contiene il nome del sovrano, riportato anche nei testi demotico e greco (vedete i tre brani di testo evidenziati in giallo nei dettagli mostrati in figura 13). E’ lo stesso scienziato del famoso "Esperimento di Young" (vedete Onde e particelle per pedoni molto curiosi ) e della "teoria tricromatica" della visione a colori (vedete Viaggio nei colori: da Newton al telefonino ) e di altro: "The last man who new everything" (L'ultimo uomo che sapeva tutto, come dice il titolo di un libro su di lui.
Sull’intuizione di Young s’innestò il contributo decisivo per la comprensione dei geroglifici dato dall’archeologo francese Jean-François Champollion , al quale è comunemente attribuito il credito della scoperta. Tramite uno studio approfondito della stele, nel 1822 egli fornì gli strumenti per convertire i geroglifici in un linguaggio corrente: chiamiamole “Regole di Champollion”. Questa conversione è comunque laboriosa, come lo è in generale quella di scritture basate su ideogrammi.
Le “Regole di Feynman” sono concise, dirette e lineari per il semplice motivo che i diagrammi di Feynman hanno la bella semplicità delle grandi idee. Questo vale non solo in Fisica. Sentite Jack Kerouac (1922-69), noto in particolare per il libro "On the road" (Sulla strada) e uno dei maggiori esponenti del movimento beat che dagli Stati Uniti scosse gli anni '60 sotto molteplici aspetti:
.
Professore Emerito di Fisica Sperimentale
Università di Napoli "Federico II"
Complesso Univ. Monte S. Angelo
Via Cintia - 80126 Napoli - Italy
Interazioni "Alla Feynman" è stato creato da P. Strolin
Interazione elettromagnetica "alla Feynman"
................
................
Per domande: autore o
Domanda a un esperto
................Quali “icone” inserire come “ouverture” a una visione della “Interazione Elettromagnetica”? Le leggi dell’elettromagnetismo classico in quattro righe: questo potremmo scrivere come didascalia di figura 1, dedicata alle “Equazioni di Maxwell”. Iniziando questo nostro percorso con il parlare della formulazione dell'Interazione elettrostatica (1785), vedremo che nel 1864 esse costituirono un grandioso e sinteticamente semplice coronamento a secoli di riflessioni e di studi sui fenomeni elettrici e magnetici nell’ambito cosiddetta “fisica classica”, per intendersi quella che era la Fisica prima della rivoluzione scientifica avvenuta nei primi decenni del Novecento. E vedremo che inquadrando teoricamente le “onde elettromagnetiche” (situandovi nientemeno che la luce) esse andarono molto oltre sia dal punto di vista teorico che da quello delle applicazioni pratiche.
| .............................................
Fig. 1. Le Equazioni di Maxwell scolpite nel basamento della sua statua a Edinburgh (2008) Immagine Wikimedia Commons | ..... | ......................
Fig. 2. Richard Feynman e i suoi diagrammi in un francobollo commemorativo (USA, 2005) Immagine R. H. Mc Kenzie - Condensed concepts |
La seconda icona può ben riguardare Richard Feynman (1918-88) e i suoi “diagrammi”. Essa è mostrata in figura 2. I diagrammi di Feynman completarono gli studi che portarono all’attuale teoria quantistica-relativistica dell’Interazione Elettromagnetica (la cosiddetta Elettro-Dinamica Quantistica, in breve QED) con un nuovo modo grafico-matematico di formulare un processo fisico, al tempo stesso rigoroso e visivamente comprensibile nel rappresentare la sua essenza. Incontreremo queste pietre miliari sulla strada che percorreremo, quella dell'Interazione Elettromagnetica, facendo tappa ove parrà particolarmente significativo.
Quest'articolo è complementare a L'enigma dell'interazione a distanza e i "quanti" e affronta l'argomento privilegiando gli aspetti concettuali e la loro storia. A essi segue Il Vuoto quantistico .
Interazione elettrostatica
La ben nota legge di Coulomb definisce quantitativamente le “forze” uguali e opposte che agiscono su due corpi elettricamente carichi in condizioni statiche, per "interazione" elettrostatica". Sottolineiamo la distinzione lessicale e sostanziale tra forza e interazione: la forza agisce su un singolo corpo, l'interazione indica il fenomeno globale che determina la trasmissione di forze ai corpi coinvolti.
La figura 3 mostra una raffinatissima “ bilancia a torsione ”, simile a quella utilizzata nel 1785 (pochi anni prima della Rivoluzione) dal nobile francese Charles Augustin de Coulomb (1736-1806) per stabilire la legge omonima della forza elettrostatica. Notate in figura 4 lo strumento usato dallo scienziato, in un dipinto che raffigura lo stesso de Coulomb. La torsione del filo costituisce la molla di un sensibilissimo dinamometro e la forza di gravità è ingegnosamente compensata tramite un bilanciere. Una bella e completa descrizione della misura è fornita nel collegamento ipertestuale fornito sopra.
| .............................................
Fig. 3. Bilancia a torsione Museo della Magnet Academy National High Magnetic Field Laboratory Immagine National High Magnetic Field Laboratory | ..... | ...................... |
Negli anni 1797-98 dello stesso periodo storico, la tecnica della bilancia a torsione fu usata anche da Henry Cavendish (1731-1810) per misurare in laboratorio la Costante di Gravitazione Universale G, fino ad allora "dedotta" dall'osservazione di fenomeni su scala terrestre o del sistema solare. Questa misura permise anche “ pesare la Terra ”: il valore della massa M della Terra fu dedotto inserendo il valore di G nell’espressione g = G M / R 2 dell'accelerazione di gravità g - individuata e misurata da Galileo (1564-1642) - ove R è il raggio della Terra. A questo proposito, non si può non ricordare la sempre sorprendente misura di R nel III secolo a.C. da parte di Eratostene . Per maggiori dettagli sulla bilancia a torsione e sulla misura di Cavendish, vedete Interazione Gravitazionale .
Perché si parla di “campi”?
Una volta appreso, l’uso di un linguaggio parlato semplifica la vita rispetto a quello dei gesti. Vale la pena apprendere anche i linguaggi della Scienza, impegnandosi e graduando l’approfondimento secondo la necessità. Una parola del linguaggio della Fisica è "campo". Il concetto di campo costituisce un’ astrazione molto generale. Come esempio, vediamone l’utilità per l’elettromagnetismo classico.
Se posta a una certa distanza da una carica elettrica Q, una carica q subisce una certa forza F e . Se la carica q raddoppia, la forza raddoppia. Quello che non cambia è il rapporto E = F e / q, ossia la forza per unità di carica: ecco nato naturalmente il campo elettrico E, che può essere definito in tutto lo spazio indipendentemente dalla carica q e in funzione unicamente dalla sua sorgente Q: la “astrazione fisica” E è più generale della forza F e .
La forza magnetica F m è detta " Forza di Lorentz ” e dipende non solo dalla carica q, ma anche dalla velocità v del corpo su cui essa si esercita. Anche per essa vale una generalizzazione in termini di un campo magnetico B, secondo la relazione F m = q v B. Il campo magnetico dipende unicamente da una sua sorgente, che però è una corrente e non una carica elettrica. Le leggi sono ben note e (nelle loro formulazioni più semplici) sono riportate praticamente in qualsiasi testo.
La forza elettrica e il relativo campo hanno la stessa direzione. Nella relazione tra forza magnetica e campo magnetico si inserisce anche la velocità, essa stessa caratterizzata da una direzione e da un verso: sono tutti "vettori". Il prodotto v B è un " prodotto vettoriale " e il suo risultato è una forza magnetica perpendicolare ad ambedue i fattori, con verso dato dalla cosiddetta "regola della mano destra".
Equazioni di Maxwell
Le equazioni di Maxwell legano il campo elettrico e quello magnetico a sorgenti costituite da cariche e correnti elettriche, in un quadro globale. Esse sono riportate in figura 1, in una formulazione che implica derivate e in cui appare un campo D, ma è collegato al campo elettrico E. Con la loro formulazione, all’età di 33 anni (ma perché lo si raffigura sempre anziano?) James Clerk Maxwell (1831-79) nel 1864 portò a compimento un processo di comprensione rigorosamente scientifica della connessione tra fenomeni elettrici e magnetici, iniziato con l'osservazione di Hans Christian Oersted (1777-1851) che una corrente elettrica genera un campo magnetico.
Maxwell operò una vera e propria “unificazione” di interazioni (elettrica e magnetica), sulla strada aperta nel 1687 dalla "Gravitazione Universale" di Isaac Newton (vedete Interazione Gravitazionale ). Così da un secolo e mezzo siamo abituati a parlare di elettro-magnetismo, unificando nell’ambito della fisica classica la descrizione dei fenomeni elettrici e magnetici in un struttura teorica comune, data appunto dalle Equazioni di Maxwell. Vedremo poi cosa significa unificazione per la fisica moderna, nell’ambito quantistico-relativistico.
Per situare l'opera di Maxwell nello svolgersi della Storia dell’umanità senza limitarsi ai suoi aspetti scientifici, ricordiamo che Thomas Alva Edison (1847-1831) inventò la lampadina a incandescenza nel 1878 e che questa tecnologia permise di realizzare il primo impianto di illuminazione pubblica tramite elettricità a New York nel 1882.
Ricordiamo altresì che il motore elettrico cosiddetto “ asincrono ”, di importanza decisiva per il suo sviluppo, fu inventato nel 1885 da Galileo Ferraris (1847-97). Secondo il noto vizio italiano egli non lo brevettò. L’industria americana Westinghouse ebbe mani libere e nel 1892 realizzò il primo motore elettrico commerciale.
Le Equazioni di Maxwell (1864) sono antecedenti ai suddetti sviluppi tecnologici ed essi stessi sono basati su leggi individuate ancora prima. Le Equazioni di Maxwell portano ben oltre sia dal punto di vista della conoscenza che da quello di applicazioni pratiche rilevanti per l'umanità, come vedremo. La Scienza precorre i tempi e apre strade che portano a tecnologie impensate.
| ............................................. | ... | ......................
Fig. 6. I naufraghi del Titanic soccorsi dal Carpathia nel 1912 dopo il primo SOS via onde radio nella storia Immagine Michel Ralph, Titanic 1912-2012 |
Equazioni di Maxwell, luce e Teoria della Relatività Speciale
Le leggi dell’elettromagnetismo, disgiunte prima di Maxwell, erano bastate per l’invenzione delle macchine elettriche. Ma vi era un’asimmetria: un campo magnetico variabile “induceva” un campo elettrico, ma vi era silenzio sul contrario. Maxwell le considerò tutte assieme in un “sistema di equazioni” e con la forza del ragionamento le simmetrizzò introducendo ∂D/∂t nel secondo membro della quarta equazione in figura 1 e simmetrizzando così ∂B/∂t nella terza equazione (per ci volesse approfondire, D è una grandezza collegata al campo elettrico E e i simboli ∂ si riferiscono a operazioni matematiche dette "derivate").
Al ruolo simmetrico dei campi elettrico e magnetico nelle Equazioni di Maxwell consegue l’esistenza di “onde elettromagnetiche”. Un’onda elettromagnetica è un "campo elettromagnetico" che si propaga e consiste in un campo elettrico E e uno magnetico B oscillanti trasversalmente alla sua direzione di propagazione e perpendicolarmente tra loro. La figura 5 mostra un'onda "polarizzata linearmente", nella quale i campi elettrico e magnetico non mutano direzione di oscillazione.
L’esistenza delle onde elettromagnetiche predette da Maxwell fu dimostrata sperimentalmente nel 1885 da Heinrich Rudolf Hertz (1857-94), che riuscì a produrle in laboratorio e a osservarle. Ora sappiamo che le onde elettromagnetiche coprono un larghissimo spettro di frequenze , che corre da quelle delle onde radio a quelle della cosiddetta “radiazione γ”.
Nel vuoto, le onde elettromagnetiche predette dalle Equazioni di Maxwell si propagano con la velocità della luce. Esse avvalorarono l’ipotesi della natura ondulatoria della luce, basata sull’ osservazione di fenomeni diffrattivi .
L’indipendenza della velocità della luce dal sistema di riferimento nelle Equazioni di Maxwell, confermata dall’esperimento di Michelson-Morley (1887), fu poi all’origine della Teoria della Relatività Speciale formulata da Albert Einstein nel 1905: vedete Simmetrie e Relatività Speciale .
La vastità delle applicazioni pratiche delle onde elettromagnetiche è enorme. Come esempio, la figura 6 mostra il Carpathia in soccorso dei naufraghi del Titanic in seguito al primo SOS via onde radio nella storia, dato nel 1912 con un radiotelegrafo installato sul Titanic dall'inventore della trasmissione via onde radio: Guglielmo Marconi (1874-1937).
Equazioni di campo per onde e particelle
La denominazione stessa lo dice, parzialmente: le Equazioni di Maxwell hanno segnato la transizione da una descrizione di fenomeni specifici in termini di “leggi” a una di valenza più ampia in termini di “Equazioni di campo”, con profilo sostanzialmente autonomo. Tuttavia, ai tempi di Maxwell, campi e oggetti sui quali essi si esercitano (particelle elementari nella fisica di oggi) erano cose ben distinte.
Nel secolo successivo, il ‘900 si sviluppò la fisica quantistica (vedete Da linee di Fraunhofer ad atomo quantistico e Onde e particelle per pedoni molto curiosi ). In particolare, i’ ipotesi di de Broglie (1924) sulla natura anche ondulatoria dell’elettrone cancellò il confine tra onde e particelle. La descrizione di ambedue in termini di campi aprì la strada per la loro coesistenza in una stessa equazione di campo, capace di descrivere le interazioni tra particelle. Lo vedremo per quella elettromagnetica.
Equazioni di campo: onde e mediatori
Nella classica interazione a distanza, il campo generato da una sorgente si stabilisce simultaneamente ovunque. La scoperta di Maxwell che il campo elettromagnetico si propaga come un'onda fu il preludio della sua fine: l'interazione è trasmessa da un'onda ed essa ha velocità finita. L'equivalenza quantistica onda-particella portò infine al concetto di “mediatore” di una interazione, cioè di una particella che la trasmette.
Dai tempi di Newton che la introdusse, l'interazione a distanza regge ancora per l'Interazione Gravitazionale, non essendovi tuttora una sua teoria quantistica. Per migliore conoscenza, vedete L'enigma dell'interazione a distanza e i "quanti" .
Interazione Elettromagnetica: formulazione quantistica
In fisica classica, il campo elettromagnetico abita nelle Equazioni di Maxwell assieme a cariche e correnti elettriche. Nella formulazione quantistica cariche e correnti sono sostituite da particelle in moto, il cui comportamento è descritto da campi tramite un'equazione quantistica-ondulatoria. Per l’Interazione Elettromagnetica, il campo elettromagnetico viene opportunamente inserito nell’equazione che descrive le particelle. Il mediatore lo traduce quantisticamente e corrisponde alla particella detta “ fotone ”.
Questo vale in particolare per l’elettrone, archetipo di particella elementare e in generale preso come riferimento. Inizialmente l'elettrone libero fu descritto tramite l’ equazione di Schrödinger (1926), limitata tuttavia a un dominio non-relativistico: andremo direttamente oltre.
| ................................................... | ... | ......................
Fig. 7b. La legge fisica dovrebbe avere bellezza matematica Manoscritto di Dirac lasciato su una lavagna della Moscow State University Da R. H. Dalitz, Biographical Memoirs of Fellows of the Royal Society, vol. 32 p. 139 (1986) Immagine Nelson Beebe - University of Utah |
Nel 1927 la famosa Equazione di Dirac fornì la prima rappresentazione relativistica del comportamento dell’elettrone, valida anche per altre particelle elementari. Essa fu concepita per superare la limitazione a energie non-relativistiche dell'equazione di Schrödinger, ma la prodigiosa intuizione di Dirac nel concepirla portò ulteriori e sorprendenti frutti.
La prima sorpresa fu l’automatica e inattesa inclusione nell’equazione stessa di una tuttora inspiegabile ma reale proprietà dell’elettrone: il suo “momento angolare di spin” (vedete Lo spin e altri sull'argomento tra i Saggi tematici ), assente nell’Equazione di Schrödinger. L’Equazione di Dirac fornì inoltre la rivoluzionaria predizione dell’esistenza di anti-particelle . La predizione di Dirac trovò conferma nel 1932 con la scoperta dell’anti-elettrone, comunemente detto “ positrone ”.
Paul Dirac fu insignito del Premio Nobel 1933 per la Fisica, assieme a Erwin Schrödinger . L'Equazione di Dirac è mostrata in figura 7a: come da sempre, l'invenzione di nuovi formalismi matematici rende semplice la rappresentazione di questioni complesse. L'Equazione di Dirac ha anche "bellezza matematica", in accordo con l'affermazione generale nel manoscritto di Dirac sulla lavagna in figura 7b.
Sulla base dell’Equazione di Dirac, gli anni ’40-’50 videro lo sviluppo della “ Elettro-Dinamica Quantistica ” (QED) e della descrizione grafica-matematica dei processi fisici tramite i diagrammi di Feynman . La QED fornisce una metodologia di calcolo che estende alle alte energie il dominio di applicazione della descrizione quantistica-relativistica dei processi elettromagnetici e porta a una straordinaria precisione la descrizione dei processi a bassa energia. Quanto ai diagrammi di Feynman, essi sono nati con la QED ma come metodo hanno un'applicabilità molto più generale.
Perle e sistemi quantistici
La pesatrice di perle (o donna che pesa dell’oro) nel dipinto di Jan Vermeer (1632-76) in figura 8 procede per approssimazioni successive, stimando di volta il pesetto da aggiungere o togliere per una pesata con la precisione desiderata.
Fig. 8. Jan Vermeer, La pesatrice di perle (dettaglio, 1662-5), National Gallery of Art, Washington - Immagine Millequadri
In fisica classica, tutto è in linea di principio rigorosamente e presuntuosamente calcolabile. A meno che non si entri in fenomeni caotici (come la turbolenza di un fluido, vedete Ali e vele ), che la apparentano a fenomeni sociali di insiemi di umani o animali (vedete La Scienza della Complessità ). Il ricorso alle approssimazioni successive è raro.
I sistemi quantistici hanno come “peccato originale” il Principio di Indeterminazione , dicendo peccato ma sempre restando il dubbio che l’imperfezione del peccato possa essere una forma di umanizzazione. I sistemi quantistici che si possono risolvere completamente sono molto pochi (uno di essi è l’atomo di Idrogeno, con un solo elettrone). Contrariamente al caso della fisica classica, nella maggior parte dei casi è quindi necessario procedere per approssimazioni successive. In particolare, si ricorre a una tecnica di calcolo che considera il fenomeno come una (piccola) perturbazione del quieto vivere del sistema, applicando il cosiddetto “ metodo perturbativo ”. La soluzione è quindi fornita per approssimazioni successive come per la pesatrice di perle, ma rigorosamente calcolate fino a raggiungere grandissime precisioni e non solo stimate.
Anche la QED è basata sul metodo perturbativo. Le predizioni sullo svolgersi di un processo fisico sono fornite sotto forma di “serie”, ossia di somme (secondo le regole quantistiche) di termini sempre più piccoli. I “diagrammi di Feynman” li rappresentano in forma grafica-matematica, ove il trattino ha lo stesso significato di quando lo vedete scritto per esempio in Vocabolario italiano-inglese. Il vocabolario per la traduzione sono le “regole di Feynman”.
Ci stiamo riferendo all’Interazione Elettro-Magnetica, ma la metodologia generale è applicabile anche nella trattazione quantistica di processi attribuibili ad altre interazioni Con opportuni accorgimenti, essa è applicabile sia a processi che avvengono in collisioni tra particelle che in processi di decadimento naturale di una particella, quale per esempio il decadimento β di un quark descritto in Interazione Elettro-Debole
In particolare, per esporre la metodologia ci riferiremo all'interazione tra due elettroni (A e
Emissione e assorbimento di un fotone e costante di accoppiamento
Nell’interazione elettrostatica come vista da de Coulomb, l’elettrone A genera simultaneamente e dappertutto un astratto campo elettrico al quale è soggetto l’elettrone B, e viceversa. Come si è detto sopra, ora sappiamo che l’interazione è trasmessa da un campo elettromagnetico ondulatorio che si propaga a velocità finita (quella della luce) e in “quanti” (una sorta di pacchetti d’onda) detti "fotoni": si deve ragionare in termini di fotoni emessi e assorbiti dagli elettroni con una certa ampiezza di probabilità.
L’ampiezza di probabilità di emissione o assorbimento del fotone è data dalla cosiddetta “costante di accoppiamento”. Guardando la figura 9 se ne capisce la denominazione: essa corrisponde al vertice in cui fotone e elettrone si collegano, o accoppiano. Come esposto in Interazioni e loro unificazione , la costante di accoppiamento è l'etichetta che definisce il tipo d’interazione: stessa costante di accoppiamento, stessa interazione. La costante di accoppiamento dell’Interazione Elettro-Magnetica è data dalla carica "e" dell’elettrone, nello speciale sistema di unità di misura comunemente usato per le particelle elementari. Notate che dicendo “elettro-magnetica” abbiamo implicitamente assunto che interazioni elettriche e magnetiche siano unificate e caratterizzate dalla stessa costante di accoppiamento: in linguaggio non quantistico lo avevano già detto le Equazioni di Maxwell.
Diagrammi di Feynman
Come detto sopra, in realtà la figura 9 è molto di più di una raffigurazione visiva di processo fisico: ne è anche una sua rappresentazione quantitativa, al pari di un’espressione matematica, è un “diagramma di Feynman”. La figura 10 mostra il primo diagramma di Feynman, riprodotto dalla sua pubblicazione originale del 1949. Da allora, essi sono diventati strumenti basilari per studi e calcoli. Nella figura, ad ogni elemento grafico (segmento di linea o vertice) del diagramma è associata la sua "traduzione" in uno dei fattori che compaiono nella espressione matematica dell'ampiezza di probabilità che il processo avvenga (indicata come “Eq. (4)” nella didascalia originale nel lavoro di Feynman, visibile in figura). Il diagramma diventa così una scrittura in lingua grafica invece che nella usuale lingua matematica, con vantaggio di immediatezza di espressione e quindi di facilità di comprensione dell'essenza fisica del processo. Vediamo meglio come questo "funziona", almeno qualitativamente.
| .............................................
Fig. 10. Traduzione degli elementi del diagramma nei fattori della corrispondente espressione matematica The Physical Review, Vol. 76 p. 769 (1949) Immagine JF Ptak Science Books | ... | ...................... |
Iniziamo con i vertici. Abbiamo visto che con una certa ampiezza di probabilità l'elettrone A può "emettere" un fotone: questa ampiezza costituisce il fattore matematico associato al vertice di emissione del fotone. Un analogo fattore matematico viene associato al vertice in cui il fotone emesso è "assorbito" dall'elettrone B.
La trasmissione (o “propagazione”) del fotone da un vertice all'alto implica una sua propria ampiezza di probabilità, determinabile dalla fomulazione matematica del suo comportamento fisico: questa ampiezza costituisce il fattore matematico associato al segmento di linea ondulata, che nel diagramma di Feyman rappresenta il fotone. Il fotone trasmesso è detto “virtuale”, in relazione al fatto che esso nasce e muore all’interno del processo e non mette piede nel mondo esterno: anche se volessimo mettere delle frecce a indicare il verso in cui si muove, non sapremmo come metterle. Questa osservazione è espressione del fatto che il processo inverso (emissione del fotone da B e assorbimento da A) è inglobato nel diagramma. Questo spiega anche l’assenza di frecce nelle figure 9 e 10, che starebbero a indicare un verso per la propagazione del fotone.
L'ampiezza di probabilità complessiva per il processo è data dal prodotto dei suddetti tre fattori (emissione-propagazione-assorbimento), e di altri fattori matematici associati ai segmenti di linea che nel diagramma rappresentano le particelle che interagiscono nel processo. Analogamente al caso del fotone, questi fattori sono determinabili dalla fomulazione matematica del loro comportamento fisico. La "probabilità" complessiva è data dal quadrato della suddetta "ampiezza di probabilità" (vedete ad esempio " Onde e particelle per pedoni molto curiosi " su questo Forum).
In pratica, le regole di corrispondenza sono state determinate una volta per tutte e costituiscono le cosiddette "Regole di Feynman", che fortunatamente stanno approssimativamente in una pagina. Per qualsiasi processo, si può quindi convenientemente partire dalla sua rapprentazione in termini di diagrammi di Feyman (con i vantaggi di immediatezza detti sopra) e quindi utilizzare le Regole di Feynman come un dizionario per tradurne gli elementi (segmento, linea ondulata o vertice) fattori matematici.
La traduzione degli elementi grafici dei diagrammi di Feynman in fattori matematici ricorda (si intende solo in linea di principio) quella della scrittura simbolica dell’antico Egitto – i geroglifici – in una scrittura fonetica. La chiave per scoprire come farlo fu fornita dalla famosa Stele di Rosetta , mostrata in figura 11: è una splendida pietra nera e incisa, un'opera di arte antica da museo di arte moderna anche nel suo stato attuale di frammento. Se la sua storia vi incuriosisce, leggete l’Appendice dal titolo I geroglifici e la Stele di Rosetta.
Come si è detto, il diagramma in figura 9 rappresenta la prima approssimazione dell'ampiezza di probabilità complessiva. Le approssimazioni successive implicano ulteriori processi di emissione e assorbimento e quindi ulteriori fattori dati dalla costante di accoppiamento. Grazie al valore relativamente piccolo della costante di accoppiamento elettro-magnetica, già la prima approssimazione si avvicina alla probabilità complessiva con una precisione dell’ordine dell’uno per cento, che in moltissimi casi è sufficiente.
Per una introduzione qualitativa ai diagrammi di Feynman, vedete Da linee di Fraunhofer ad atomo quantistico . Per approfondimenti sugli ordini di approssimazione seguenti, vedete Il Vuoto quantistico .
Verifiche sperimentali
Per verificare la QED con la massima accuratezza, si è innescata una gara – tuttora in corso - tra fisici teorici e sperimentali: i teorici introducendo successivi livelli di approssimazione, gli sperimentali conducendo esperimenti sempre più raffinati e precisi. Si é così giunti a verificare la QED con la strabiliante accuratezza di 10 parti per miliardo !
Come già notato, a fine Settecento la legge di Coulomb era la conoscenza di frontiera corrispondente alla QED. La precisione della misura, e inizialmente anche la giustificazione sperimentale delle conclusioni tratte, fu controversa ed è tuttora oggetto di dibattito nell’ambito della Storia della Scienza. Essa fu comunque straordinaria per i mezzi di allora. Paragonate un suo valore indicativo, dell’ordine del 5%, alle 10 parti per miliardo raggiunte nella verifica della QED. Ogni commento sul progresso effettuato è superfluo.
Il discorso continua in …
Leggete Interazione Elettro-Debole e Simmetrie e interazioni fondamentali . Troverete che l’Interazione Elettromagnetica e la cosiddetta Debole sono ora unificate nella “Interazione Elettro-Debole”. Troverete inoltre che si può ribaltare la genesi della QED: da teoria sviluppatasi in base a una storia di osservazioni sperimentali, essa può essere formulata “a tavolino” imponendo una opportuna simmetria.
Collegamenti e riferimenti bibliografici
Richard P. Feynman, QED: the strange theory of light and matter - QED: la strana teoria della luce e della materia , Editore Princeton University Press (1965) - Adelphi (1989)
Appendice: I geroglifici e la Stele di Rosetta
I diagrammi di Feynman usano un linguaggio grafico simbolico traducibile in un’espressione matematica. Abbiamo caratteri grafici simbolici anche per le lingue scritte: abitualmente usiamo degli astratti caratteri fonetici, ma in lingue orientali si usano ideogrammi e nell’antico Egitto si usavano geroglifici .
Per secoli l’interpretazione e la traduzione dei geroglifici ha affascinato e impegnato gli studiosi. Citiamo in particolare il grande umanista e scienziato Athanasius Kircher (1602-80), di poco posteriore a Galileo. Nel linguaggio scientifico di oggi possiamo dire che ancora mancavano "dati sperimentali" che fornissero una chiave interpretativa e permettessero di andare oltre una metodologia essenzialmente speculativa.
| ...............................................
Fig. 12. Napoleone Bonaparte a Giza davanti alla Sfinge (1867- Dipinto di Jean-Léon Gérôme (1824-1904) Hearst Castle, San Simeon (California) Immagine Wikipedia | ... | ......................
Fig. 13. Stele di Rosetta (dettagli) Dall'alto al basso: geroglifici, demotico e greco Decreto tolemaico del 196 a.C. British Museum (Londra) Immagini estratte da Histoforum |
La chiave decisiva per l’interpretazione dei geroglifici fu offerta dal ritrovamento nel 1799 della Stele di Rosetta (figura 11) nel corso della campagna napoleonica d’Egitto (1798-1801), al cui seguito vi era un folto stuolo studiosi. Il fascino dell'antico Egitto era grande anche per Napoleone Bonaparte, come simbolicamente mostrato nella suggestiva figura 12. Il rovescio della medaglia fu la spoliazione di numerosi capolavori. La stele - consegnata agli inglesi dopo la disfatta francese ad Abukir e ora al British Museum - riporta un decreto tolemaico del secondo secolo a.C. scritto in tre differenti grafie: egizia geroglifica, egizia demotica e greca.
Nel 1814 il grande scienziato Thomas Young per primo intuì che un cartiglio nel testo geroglifico contiene il nome del sovrano, riportato anche nei testi demotico e greco (vedete i tre brani di testo evidenziati in giallo nei dettagli mostrati in figura 13). E’ lo stesso scienziato del famoso "Esperimento di Young" (vedete Onde e particelle per pedoni molto curiosi ) e della "teoria tricromatica" della visione a colori (vedete Viaggio nei colori: da Newton al telefonino ) e di altro: "The last man who new everything" (L'ultimo uomo che sapeva tutto, come dice il titolo di un libro su di lui.
Sull’intuizione di Young s’innestò il contributo decisivo per la comprensione dei geroglifici dato dall’archeologo francese Jean-François Champollion , al quale è comunemente attribuito il credito della scoperta. Tramite uno studio approfondito della stele, nel 1822 egli fornì gli strumenti per convertire i geroglifici in un linguaggio corrente: chiamiamole “Regole di Champollion”. Questa conversione è comunque laboriosa, come lo è in generale quella di scritture basate su ideogrammi.
Le “Regole di Feynman” sono concise, dirette e lineari per il semplice motivo che i diagrammi di Feynman hanno la bella semplicità delle grandi idee. Questo vale non solo in Fisica. Sentite Jack Kerouac (1922-69), noto in particolare per il libro "On the road" (Sulla strada) e uno dei maggiori esponenti del movimento beat che dagli Stati Uniti scosse gli anni '60 sotto molteplici aspetti:
“One day I will find the right words, and they will be simple”
Un giorno troverò le parole giuste, e saranno semplici
(Jack Kerouac, The Dharma burns - I vagabondi del Dharma, 1958)
.Un giorno troverò le parole giuste, e saranno semplici
(Jack Kerouac, The Dharma burns - I vagabondi del Dharma, 1958)
.
Professore Emerito di Fisica Sperimentale
Università di Napoli "Federico II"
Complesso Univ. Monte S. Angelo
Via Cintia - 80126 Napoli - Italy
Ultima Modifica 9 Anni 1 Mese fa da Paolo.
Si prega Accesso a partecipare alla conversazione.
Tempo creazione pagina: 0.669 secondi