Da linee di Fraunhofer ad atomo quantistico
- P. Strolin
-
Autore della discussione
- Offline
- Premium Utente
-
Less
Di più
11 Anni 5 Mesi fa - 9 Anni 2 Mesi fa #147
da P. Strolin
Da linee di Fraunhofer a Universo in espansione parla della scoperta (nel 1814) che lo spettro cromatico della luce solare contiene numerose linee scure: le “linee di Fraunhofer”. Illustra poi come da questo “seme” nacquero l’Astrofisica e la Cosmologia di oggi. In quest’articolo vediamo come le regolarità matematiche delle linee di Fraunhofer furono il primo segnale di quantizzazione dei livelli energetici degli elettroni atomici e quindi il “seme” della rivoluzione scientifica che ha portato all’atomo quantistico.
Nelle profondità essenziali della Scienza, ove stanno le radici dei fenomeni, troviamo le "costanti". La costante della Fisica Quantistica è la "costante di Planck". Ragioniamo per pietre miliari. Essa nasce nel 1900 dall’ipotesi di quantizzazione dello spettro del “corpo nero” , empiricamente formulata da Planck per riprodurne le fin ad allora inspiegabili caratteristiche. E’ la base della " quantizzazione " della radiazione elettromagnetica (Einstein, 1905) e di quella dei momenti angolari (Bohr, 1913). Appare nel cosiddetto " dualismo onda-particella ", ossia la descrizione delle particelle tramite onde e viceversa (de Broglie, 1924). Regola il “ principio di indeterminazione " (Heisenberg, 1927).
Per tutto questo la costante di Planck entra nelle leggi che descrivono il comportamento delle particelle, a iniziare dalla equazione di Schrödinger (1927) valida particelle non relativistiche quali sono gli elettroni atomici.
La costante di Planck è la base comune di questo e dell'articolo gemello Da linee di Fraunhofer a Universo in espansione . L’ampiezza della sua portata è tale che essa gioca un ruolo fondamentale nelle teorie di " Grande Unificazione ".
Duecento anni di Scienza
E’ oggi impensabile vivere senza l’elettronica e altre tecnologie basate sulla Fisica Quantistica. Onde e particelle per pedoni molto curiosi espone come essa riesce a spiegare il comportamento degli elettroni (e in generale delle particelle elementari) descrivendone lo stato in termini di “ampiezza di probabilità”, e non di coordinate e quantità di moto precise come è possibile limitatamente al dominio di validità della fisica classica. Gli elettroni in un atomo non percorrono “orbite” come in un sistema planetario. La loro energia è “quantizzata”, nel senso che può assumere solo determinati valori. In generale, essi possono trovarsi solo in determinati “stati quantici”. A ciascun stato quantico corrisponde una distribuzione spaziale di “densità di probabilità” propria di un “ orbitale ”.
Le tecnologie elettroniche di oggi sono state sviluppate in base alla suddetta visione quantistica, senza tuttavia che un orbitale fosse mai stato “visto”. Essi erano stati ma solo ricostruiti e rappresentati mediante calcoli teorici. La stessa rappresentazione mentale e una visione grafica dei fenomeni quantistici non sono immediate, dato la nostra esperienza sensoriale è limitata al mondo macroscopico. Qualche riflessione è sviluppata in Pensare in quantistico .
Duecento anni di Scienza collegano la figura 1 alla figura 2. La figura 1 riprende da Da linee di Fraunhofer a Universo in espansione la scoperta delle linee di Fraunhofer nel 1814. La figura 2 mostra la prima “immagine” della densità di probabilità dell’elettrone nell’atomo di Idrogeno eccitato, ricostruita mediante un "microscopio quantistico" di nuova concezione e pubblicata su Physical Review Letters nel 2013. Gli elettroni situati su orbitali di stati eccitati dell’atomo di Idrogeno sono stati estratti mediante un fascio laser, e immessi in una lente d’ingrandimento elettrostatico per ottenere un’immagine delle corrispondenti densità di probabilità. Per maggiori dettagli, potete consultare l’articolo su io9 dal quale è tratta la figura.
Serie spettroscopiche
Focalizziamo l’attenzione sull’Idrogeno. Al tempo in cui furono studiate le linee di Fraunhofer, il nucleo atomico non era ancora stato scoperto da Rutherford (questo avvenne nel 1909) e l’Idrogeno non era ancora visto come l’atomo più semplice (un protone e un elettrone). Esso era comunque l’elemento chimico più elementare, come dice la Tavola Periodica degli Elementi redatta da Mendeleev nel 1869.
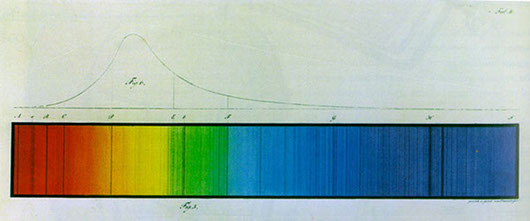
L’osservazione delle prime tre linee di assorbimento dell’Idrogeno nel visibile da parte di Jonas Ångstrom nel 1862 fu seguita dall’osservazione di altre linee e iniziarono ad apparire delle “regolarità” nella loro sequenza (figura 3).
Nel 1885 Johann Balmer scoprì che le linee osservate nel visibile per l’Idrogeno (figura 3) sono rappresentate da una serie, la cosiddetta “ serie di Balmer ”. Altre serie furono poi individuate in altri domini dello spettro.
Nel 1888 Johannes Rydberg individuò una rappresentazione delle serie trovate, valida in tutti i domini dello spettro dell’Idrogeno. La rappresentazione è data dalla “ formula di Rydberg ”:
.......................................
dove:
R è la “costante di Rydberg” propria dell’Idrogeno;
n 1 è un numero intero maggiore o uguale a 1, che caratterizza la serie e assume il valore 2 per la serie di Balmer valida nel visibile;
n 2 è un numero intero maggiore di n 1 , che determina lo sviluppo della serie aumentando di una unità alla volta.
La formula di Rydberg, valida per l'Idrogeno, risultò adattabile ad altri elementi chimici, apportando appropriate modifiche.
Segnale di nuova fisica
La formula della serie di Balmer e la sua generalizzazione da parte di Rydberg erano puramente empiriche, essendo unicamente basate su dati sperimentali. La loro sconcertante semplicità rendeva l’enigma ancora più profondo. Esse apparivano come un segnale anticipatore di fisica totalmente nuova. La fisica quantistica, ancora non percepibile, inviava un segnale che preludeva all’ingresso in campo della “ costante di Planck ” e della “quantizzazione” dei livelli energetici degli elettroni atomici.
Inspiegabili fatti sperimentali
Le Linee di Fraunhofer e la loro descrizione con la formula di Rydberg non erano il solo “fatto sperimentale” inspiegabile in base alla fisica classica.
Per definizione, un “ corpo nero ” emette radiazione elettromagnetica per effetto termico ma è caratterizzato dall’assenza di riflessioni, come una cavità in comunicazione con l’esterno solo tramite un piccolo orifizio. Lo spettro delle radiazioni emesse era difforme rispetto alla previsione della fisica classica.
Nell’ effetto fotoelettrico la capacità della radiazione elettromagnetica di estrarre elettroni presentava una misteriosa “soglia” dipendente dalla sua frequenza e non dalla sua intensità: sotto la frequenza di soglia, di colpo assolutamente nulla.
Nasce la costante di Planck
Nel 1900 il 42enne Max Planck (1858-1947) spiegò le caratteristiche dello spettro del corpo nero formulando empiricamente l’ ipotesi che per ogni frequenza l’energia complessiva della radiazione sia “quantizzata”, potendo assumere solo valori discreti e multipli di una nuova costante moltiplicata per la frequenza. Cinque anni dopo (vedi sotto) le fu dato il nome di “costante di Planck” e fu denotata con il simbolo h.
Nel 1905 il 26enne Albert (ovviamente Einstein, 1879-1955) andò oltre. Egli ipotizzò che la radiazione sia emessa e assorbita in singoli pacchetti (detti “quanti”), ciascuno con energia E = h ν ove ν è la frequenza della radiazione. I quanti della radiazione elettromagnetica (“particelle di luce”) sono correntemente chiamati “ fotoni ”.
La quantizzazione dello spettro del corpo nero è così interpretata come un effetto cumulativo di singoli quanti. Viene spiegato anche l’effetto fotoelettrico. La misteriosa frequenza di soglia si traduce in una plausibile energia di soglia, corrispondente all’energia minima da conferire agli elettroni affinché essi superino la barriera di energia potenziale che li confina e possano uscirne liberi.
La costante di Planck h si avviava così a diventare regina della nuova “ Fisica Quantistica ”.
L’atomo di Bohr
Nel 1909, a 38 anni di età Ernest Rutherford (1871-1937) aveva scoperto che la massa dell’atomo è concentrata in un piccolissimo nucleo. I “ modelli planetari ” dell’atomo contemplavano elettroni orbitanti come pianeti nel sistema solare. Ma le leggi dell’elettrodinamica classica prevedono l’emissione di energia da particelle elettricamente cariche che seguono una traiettoria curva. Nei modelli planetari, gli elettroni perdendo energia dovrebbero cadere a spirale sul nucleo. La fisica classica non riusciva a spiegare l’atomo.
La rivoluzione operata da Nicola Copernico (1473-1543) portò a una visione “eliocentrica” (figura 4). Giovanni Keplero (1571-1630) individuò le leggi empiriche che regolano le orbite dei pianeti e completò la visione fenomenologica del sistema solare.
Per l’atomo, un corrispondente livello di conoscenza fu raggiunto nel 1913 con il cosiddetto “ modello di Bohr ”, valido unicamente per l’atomo di Idrogeno e rappresentato in figura 5. Avendo come punto di partenza l’atomo “nucleocentrico” di Rutherford, a 28 anni di età Niels Bohr (1885-1962) operò una sintesi fenomenologica basata sulle serie spettroscopiche (di natura empirica), sull’ipotesi quantistica di Planck e sulla soglia riscontrata per l’effetto fotoelettrico.
Nel modello di Bohr per l’atomo di Idrogeno, si ipotizza che l'elettrone sia vincolato a mantenersi su una delle orbite fisse corrispondenti a momenti angolari quantizzati e multipli di h /2π. I valori possibili per il momento angolare sono quindi dati da n h /2π, ove n è un numero intero maggiore o eguale a 1. Esso è chiamato “numero quantico principale”.
Corrispondentemente, si trova che l’energia totale (potenziale più cinetica) dell’elettrone assume valori quantizzati E n e proporzionali a – 1 / n 2 , ove n è un numero intero positivo e a meno di una costante additiva. A n = 1 corrisponde lo stato quantico di energia minima. L’elettrone è libero (E n = 0) per un valore infinito di n. Si tenga presente che gli elettroni atomici sono non relativistici, dato che hanno energie dell’ordine della decina di elettron-Volt (eV) e quindi cinque ordini di grandezza più piccole della loro massa (0.5 MeV).
Il modello di atomico di Bohr vale - come si è detto - unicamente per l’atomo di Idrogeno, ma il concetto di quantizzazione dei livelli energetici degli elettroni è di validità generale.
Atomo di Bohr e ipotesi ondulatoria
La figura 9 mostra che le vibrazioni di una corda (per esempio di violino) fissata alle estremità sono caratterizzate dalle presenza delle cosiddette “ onde stazionarie ”, che per definizione si mantengono nel tempo. Esse corrispondono ai cosiddetti "modi principali" di oscillazione e sono quantizzate”: la lunghezza d’onda λ può assumere solo determinati valori, con l sia multiplo di ½ λ.
Nel 1924 a soli 26 anni Louis de Broglie (1892-1987) nella sua tesi di dottorato formulò l’ ipotesi ondulatoria e fece emergere la rappresentazione dell’elettrone come un’onda. Secondo questa rappresentazione, nell’atomo di Bohr le orbite hanno proprietà analoghe a quelle dei modi normali delle corde vibranti: esse sono stazionarie e quantizzate. Come mostrato in figura 10, si ritrova la stessa relazione di quantizzazione nella quale l/λ è multiplo di ½, tramite un fattore n come numero quantico e con l che ora rappresenta la circonferenza dell’orbita.
Orbitali elettronici
Un descrizione quantitativa ed esauriente del moto dei pianeti necessita un’equazione del moto. Vi giunse Isaac Newton (1642-1727) con la Gravitazione Universale applicata alle conoscenze precedenti.
Oltre che dal numero quantico principale n già trovato con l’atomo di Bohr, gli orbitali elettronici sono contraddistinti dal “numero quantico orbitale o azimutale” l (con valori possibili eguali a 0, 1, 2, … ma al massimo n-1) e dal “numero quantico magnetico” m l (con per valori possibili i numeri interi che vanno da -l a +l.
La natura degli orbitali elettronici è stata esposta all’inizio del percorso che abbiamo qui seguito. Le posizioni in cui si può trovare un elettrone atomico sono descritte da una distribuzione di densità di probabilità, che nello spazio può essere rappresentata da una “nube elettronica”. La figura 11 mostra il risultato di calcoli teorici che danno la nube elettronica corrispondente all’orbitale detto “1s” dell’atomo di Idrogeno. Questo è l’orbitale a energia più bassa (n = 1, da cui "1") e con l = 0, il che lo rende spazialmente simmetrico (da cui la denominazione “s”).
Abbiamo dovuto giungere a nostri giorni per avere la prima immagine di un orbitale elettronico, mostrata in figura 2.
Natura facit saltus
" Natura non facit saltus " (la natura non fa salti) è una locuzione latina. Essa deriva dal principio, di remota origine, che in Natura la gradualità impera.
Nella forma “Tout va par degrés dans la nature, et rien par saut” (tutto va per gradi nella natura, e niente con salto) la sentenza è presente nell’opera Nouveaux essais (IV, 16, 12) pubblicata da Gottfried von Leibniz (1646-1716) nel 1704. Egli e Isaac Newton (1646-1727) fondarono il “ Calcolo infinitesimale ”, con le note (almeno di fama) “derivate” e gli ugualmente noti “integrali”. Coerentemente con il principio di gradualità, tale calcolo è basato sull'assioma che ogni grandezza fisica può assumere valori appartenenti a un continuum e quindi ammette variazioni di entità piccolissima o addirittura idealmente tendente a zero (in linguaggio matematico "infinitesima"). in particolare, il calcolo infinitesimale permise accuratissimi calcoli delle orbite dei corpi celesti. Come conseguenza del suddetto assioma, le orbite anche matematicamente possibili appartengono a un continuum.
Le orbite degli elettroni nell’atomo "alla Bohr" e gli orbitali nell’atomo “alla Schrödinger” non ammettono l'appartenenza a un continuum, ma piuttosto a un insieme di stati discreti caratterizzati da "numeri quantici". Nel mondo microscopico il principio di gradualità è sovvertito e la Fisica Quantistica mostra il suo temperamento rivoluzionario, tuttora vivo: Natura facit saltus.
Concludendo
Abbiamo constatato che le linee di Fraunhofer sono alle origini di straordinari sviluppi in vari domini della Scienza e in particolare in Fisica, Chimica, Astrofisica e Cosmologia. Ne abbiamo tratto ispirazione e motivo per delineare alcuni di essi in Da linee di Fraunhofer a Universo in espansione e in quest’articolo. A loro volta, dagli sviluppi scientifici sono nate e continuano a crescere Tecnologie e applicazioni pratiche ormai integrate nella vita umana, anche in suoi aspetti essenziali.
Collegamenti
Peter Atkins e Loretta Jones, Dall’atomo alle soluzioni , La Chimica di Atkins, Ed. Zanichelli Scuola
La fisica moderna , Sapere.it
Ray F. Egerton, Optical spectroscopy and Bohr’s model of the atom , Portland State University
Unità didattica di Storia della Spettroscopia – Università di Bari, Storia della Spettroscopia
James Schombert, Microscopic World , 21st Century Science , University of Oregon
.
Professore Emerito di Fisica Sperimentale
Università di Napoli "Federico II"
Complesso Univ. Monte S. Angelo
Via Cintia - 80126 Napoli - Italy
Da linee di Fraunhofer ad atomo quantistico è stato creato da P. Strolin
Da linee di Fraunhofer ad atomo quantistico
........
Clara Guadagni e
Paolo Strolin
................
Per domande: autori o
Domanda a un esperto
................Da linee di Fraunhofer a Universo in espansione parla della scoperta (nel 1814) che lo spettro cromatico della luce solare contiene numerose linee scure: le “linee di Fraunhofer”. Illustra poi come da questo “seme” nacquero l’Astrofisica e la Cosmologia di oggi. In quest’articolo vediamo come le regolarità matematiche delle linee di Fraunhofer furono il primo segnale di quantizzazione dei livelli energetici degli elettroni atomici e quindi il “seme” della rivoluzione scientifica che ha portato all’atomo quantistico.
Nelle profondità essenziali della Scienza, ove stanno le radici dei fenomeni, troviamo le "costanti". La costante della Fisica Quantistica è la "costante di Planck". Ragioniamo per pietre miliari. Essa nasce nel 1900 dall’ipotesi di quantizzazione dello spettro del “corpo nero” , empiricamente formulata da Planck per riprodurne le fin ad allora inspiegabili caratteristiche. E’ la base della " quantizzazione " della radiazione elettromagnetica (Einstein, 1905) e di quella dei momenti angolari (Bohr, 1913). Appare nel cosiddetto " dualismo onda-particella ", ossia la descrizione delle particelle tramite onde e viceversa (de Broglie, 1924). Regola il “ principio di indeterminazione " (Heisenberg, 1927).
Per tutto questo la costante di Planck entra nelle leggi che descrivono il comportamento delle particelle, a iniziare dalla equazione di Schrödinger (1927) valida particelle non relativistiche quali sono gli elettroni atomici.
La costante di Planck è la base comune di questo e dell'articolo gemello Da linee di Fraunhofer a Universo in espansione . L’ampiezza della sua portata è tale che essa gioca un ruolo fondamentale nelle teorie di " Grande Unificazione ".
| ........................................
Fig. 1. Le linee nere nello spettro della luce solare osservate da Fraunhofer nel 1814 Denkschriften der Akademie der Wissenschaften zu München, Vol. 5, Table II, Munich 1817 Deutsches Museum, Munich, Germany - Immagine Exploring Cosmos – UC Irvine | ..... | .......................................
Fig. 2. Densità di probabilità dell’elettrone nell’atomo di Idrogeno eccitato, ricostruita con un microscopio quantistico Immagine io9 |
Duecento anni di Scienza
E’ oggi impensabile vivere senza l’elettronica e altre tecnologie basate sulla Fisica Quantistica. Onde e particelle per pedoni molto curiosi espone come essa riesce a spiegare il comportamento degli elettroni (e in generale delle particelle elementari) descrivendone lo stato in termini di “ampiezza di probabilità”, e non di coordinate e quantità di moto precise come è possibile limitatamente al dominio di validità della fisica classica. Gli elettroni in un atomo non percorrono “orbite” come in un sistema planetario. La loro energia è “quantizzata”, nel senso che può assumere solo determinati valori. In generale, essi possono trovarsi solo in determinati “stati quantici”. A ciascun stato quantico corrisponde una distribuzione spaziale di “densità di probabilità” propria di un “ orbitale ”.
Le tecnologie elettroniche di oggi sono state sviluppate in base alla suddetta visione quantistica, senza tuttavia che un orbitale fosse mai stato “visto”. Essi erano stati ma solo ricostruiti e rappresentati mediante calcoli teorici. La stessa rappresentazione mentale e una visione grafica dei fenomeni quantistici non sono immediate, dato la nostra esperienza sensoriale è limitata al mondo macroscopico. Qualche riflessione è sviluppata in Pensare in quantistico .
Duecento anni di Scienza collegano la figura 1 alla figura 2. La figura 1 riprende da Da linee di Fraunhofer a Universo in espansione la scoperta delle linee di Fraunhofer nel 1814. La figura 2 mostra la prima “immagine” della densità di probabilità dell’elettrone nell’atomo di Idrogeno eccitato, ricostruita mediante un "microscopio quantistico" di nuova concezione e pubblicata su Physical Review Letters nel 2013. Gli elettroni situati su orbitali di stati eccitati dell’atomo di Idrogeno sono stati estratti mediante un fascio laser, e immessi in una lente d’ingrandimento elettrostatico per ottenere un’immagine delle corrispondenti densità di probabilità. Per maggiori dettagli, potete consultare l’articolo su io9 dal quale è tratta la figura.
Serie spettroscopiche
Focalizziamo l’attenzione sull’Idrogeno. Al tempo in cui furono studiate le linee di Fraunhofer, il nucleo atomico non era ancora stato scoperto da Rutherford (questo avvenne nel 1909) e l’Idrogeno non era ancora visto come l’atomo più semplice (un protone e un elettrone). Esso era comunque l’elemento chimico più elementare, come dice la Tavola Periodica degli Elementi redatta da Mendeleev nel 1869.
L’osservazione delle prime tre linee di assorbimento dell’Idrogeno nel visibile da parte di Jonas Ångstrom nel 1862 fu seguita dall’osservazione di altre linee e iniziarono ad apparire delle “regolarità” nella loro sequenza (figura 3).
| .................................................................................
Fig. 3. Lo spettro dell’Idrogeno, con lunghezza d’onda decrescente verso destra. Le prime quattro linee da sinistra cadono nel visibile Immagine Storia della Spettroscopia - Università di Bari | ..... | ....................................... Prendete la sequenza di numeri 1, 1/2, 1/3, 1/4, …. . Si capisce subito che la regolarità di questa sequenza matematica è regolata da una legge. In casi simili, il fisico vede un possibile segnale di nuova fisica da scoprire. L’osservazione delle regolarità delle linee di Fraunhofer fu quindi accompagnata dalla ricerca di una rappresentazione matematica sequenzialedelle corrispondenti lunghezze d’onda λ. In spettroscopia, questa rappresentazione matematica delle regolarità delle linee spettrali viene dato il nome di “serie”. |
Nel 1885 Johann Balmer scoprì che le linee osservate nel visibile per l’Idrogeno (figura 3) sono rappresentate da una serie, la cosiddetta “ serie di Balmer ”. Altre serie furono poi individuate in altri domini dello spettro.
Nel 1888 Johannes Rydberg individuò una rappresentazione delle serie trovate, valida in tutti i domini dello spettro dell’Idrogeno. La rappresentazione è data dalla “ formula di Rydberg ”:
.......................................
dove:
R è la “costante di Rydberg” propria dell’Idrogeno;
n 1 è un numero intero maggiore o uguale a 1, che caratterizza la serie e assume il valore 2 per la serie di Balmer valida nel visibile;
n 2 è un numero intero maggiore di n 1 , che determina lo sviluppo della serie aumentando di una unità alla volta.
La formula di Rydberg, valida per l'Idrogeno, risultò adattabile ad altri elementi chimici, apportando appropriate modifiche.
Segnale di nuova fisica
La formula della serie di Balmer e la sua generalizzazione da parte di Rydberg erano puramente empiriche, essendo unicamente basate su dati sperimentali. La loro sconcertante semplicità rendeva l’enigma ancora più profondo. Esse apparivano come un segnale anticipatore di fisica totalmente nuova. La fisica quantistica, ancora non percepibile, inviava un segnale che preludeva all’ingresso in campo della “ costante di Planck ” e della “quantizzazione” dei livelli energetici degli elettroni atomici.
Inspiegabili fatti sperimentali
Le Linee di Fraunhofer e la loro descrizione con la formula di Rydberg non erano il solo “fatto sperimentale” inspiegabile in base alla fisica classica.
Per definizione, un “ corpo nero ” emette radiazione elettromagnetica per effetto termico ma è caratterizzato dall’assenza di riflessioni, come una cavità in comunicazione con l’esterno solo tramite un piccolo orifizio. Lo spettro delle radiazioni emesse era difforme rispetto alla previsione della fisica classica.
Nell’ effetto fotoelettrico la capacità della radiazione elettromagnetica di estrarre elettroni presentava una misteriosa “soglia” dipendente dalla sua frequenza e non dalla sua intensità: sotto la frequenza di soglia, di colpo assolutamente nulla.
Nasce la costante di Planck
Nel 1900 il 42enne Max Planck (1858-1947) spiegò le caratteristiche dello spettro del corpo nero formulando empiricamente l’ ipotesi che per ogni frequenza l’energia complessiva della radiazione sia “quantizzata”, potendo assumere solo valori discreti e multipli di una nuova costante moltiplicata per la frequenza. Cinque anni dopo (vedi sotto) le fu dato il nome di “costante di Planck” e fu denotata con il simbolo h.
Nel 1905 il 26enne Albert (ovviamente Einstein, 1879-1955) andò oltre. Egli ipotizzò che la radiazione sia emessa e assorbita in singoli pacchetti (detti “quanti”), ciascuno con energia E = h ν ove ν è la frequenza della radiazione. I quanti della radiazione elettromagnetica (“particelle di luce”) sono correntemente chiamati “ fotoni ”.
La quantizzazione dello spettro del corpo nero è così interpretata come un effetto cumulativo di singoli quanti. Viene spiegato anche l’effetto fotoelettrico. La misteriosa frequenza di soglia si traduce in una plausibile energia di soglia, corrispondente all’energia minima da conferire agli elettroni affinché essi superino la barriera di energia potenziale che li confina e possano uscirne liberi.
La costante di Planck h si avviava così a diventare regina della nuova “ Fisica Quantistica ”.
| ........................................ | ..... | ...........................................................
Fig. 5. Atomo di Idrogeno secondo Bohr e livelli energetici dell’elettrone Immagine Brockport High School – New York A sinistra Fig. 4. Il sistema solare nel manoscritto di Nicolas Copernicus De revolutionibus orbium coelestium (1520-41, pubblicato nel 1543) Jagiellonian Library , Kracow - Immagine Istituto Calvino, Milano |
L’atomo di Bohr
Nel 1909, a 38 anni di età Ernest Rutherford (1871-1937) aveva scoperto che la massa dell’atomo è concentrata in un piccolissimo nucleo. I “ modelli planetari ” dell’atomo contemplavano elettroni orbitanti come pianeti nel sistema solare. Ma le leggi dell’elettrodinamica classica prevedono l’emissione di energia da particelle elettricamente cariche che seguono una traiettoria curva. Nei modelli planetari, gli elettroni perdendo energia dovrebbero cadere a spirale sul nucleo. La fisica classica non riusciva a spiegare l’atomo.
La rivoluzione operata da Nicola Copernico (1473-1543) portò a una visione “eliocentrica” (figura 4). Giovanni Keplero (1571-1630) individuò le leggi empiriche che regolano le orbite dei pianeti e completò la visione fenomenologica del sistema solare.
Per l’atomo, un corrispondente livello di conoscenza fu raggiunto nel 1913 con il cosiddetto “ modello di Bohr ”, valido unicamente per l’atomo di Idrogeno e rappresentato in figura 5. Avendo come punto di partenza l’atomo “nucleocentrico” di Rutherford, a 28 anni di età Niels Bohr (1885-1962) operò una sintesi fenomenologica basata sulle serie spettroscopiche (di natura empirica), sull’ipotesi quantistica di Planck e sulla soglia riscontrata per l’effetto fotoelettrico.
Nel modello di Bohr per l’atomo di Idrogeno, si ipotizza che l'elettrone sia vincolato a mantenersi su una delle orbite fisse corrispondenti a momenti angolari quantizzati e multipli di h /2π. I valori possibili per il momento angolare sono quindi dati da n h /2π, ove n è un numero intero maggiore o eguale a 1. Esso è chiamato “numero quantico principale”.
Corrispondentemente, si trova che l’energia totale (potenziale più cinetica) dell’elettrone assume valori quantizzati E n e proporzionali a – 1 / n 2 , ove n è un numero intero positivo e a meno di una costante additiva. A n = 1 corrisponde lo stato quantico di energia minima. L’elettrone è libero (E n = 0) per un valore infinito di n. Si tenga presente che gli elettroni atomici sono non relativistici, dato che hanno energie dell’ordine della decina di elettron-Volt (eV) e quindi cinque ordini di grandezza più piccole della loro massa (0.5 MeV).
Il modello di atomico di Bohr vale - come si è detto - unicamente per l’atomo di Idrogeno, ma il concetto di quantizzazione dei livelli energetici degli elettroni è di validità generale.
| ................................................................................................................
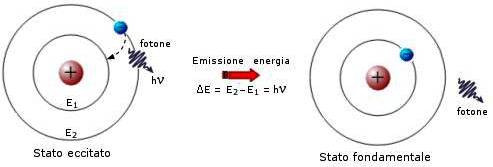
Fig. 6. L’atomo di Bohr e le linee di assorbimento - Immagine Chimica-online Fig. 7. L’atomo di Bohr e le linee di emissione - Immagine Chimica-online
Fig. 8. L’effetto fotoelettrico in fisica quantistica - Immagine
LEM - Univ. Torino
| ....... | ........................................................... Effetto fotoelettrico e linee di Fraunhofer nell’atomo di Bohr Come conseguenza della quantizzazione dei livelli energetici degli elettroni atomici, le linee di assorbimento e di emissione sono dovute a transizioni di un elettrone tra due livelli energetici ben definiti E 1 < E 2 . Il livello energetico iniziale è E 1 per l’assorbimento (figura 6) e E 2 per l’emissione (figura 7). Consideriamo in particolare l’atomo di Idrogeno, per il quale vale il modello di Bohr. L’assorbimento (figura 6) corrisponde alla transizione da uno stato con numero quantico principale n 1 a un altro con n 2 > n 1 . La proporzionalità dell’inverso della lunghezza d’onda λ della radiazione assorbita all’espressione tra parentesi al secondo membro della formula di Rydberg si ritrova tenendo presente che esso è proporzionale alla frequenza ν (essendo c/λ = ν) e quindi all’energia assorbita ΔE = h ν, con E n proporzionale a – 1 / n 2 . Il modello atomico di Bohr fa ritrovare anche il corretto valore della costante di Rydberg. Ragionamenti analoghi valgono per gli spettri di emissione (figura 7). La quantizzazione dei livelli energetici degli elettroni spiega la soglia in frequenza (o energia) per l’effetto fotoelettrico come illustrato in figura 8. Essa proviene dal fatto che per estrarre un elettrone dalla sua orbita è necessario comunicargli un’energia almeno pari a En. |
Atomo di Bohr e ipotesi ondulatoria
La figura 9 mostra che le vibrazioni di una corda (per esempio di violino) fissata alle estremità sono caratterizzate dalle presenza delle cosiddette “ onde stazionarie ”, che per definizione si mantengono nel tempo. Esse corrispondono ai cosiddetti "modi principali" di oscillazione e sono quantizzate”: la lunghezza d’onda λ può assumere solo determinati valori, con l sia multiplo di ½ λ.
| ........................................
Fig. 9. Gli stati stazionari delle corde vibranti Immagine Univ. Wisconsin Platteville | ... | .......................................
Fig. 10. Le orbite stazionarie dell’elettrone nell'atomo di Bohr secondo l’ipotesi ondulatoria Immagine Univ. Wisconsin Platteville |
Nel 1924 a soli 26 anni Louis de Broglie (1892-1987) nella sua tesi di dottorato formulò l’ ipotesi ondulatoria e fece emergere la rappresentazione dell’elettrone come un’onda. Secondo questa rappresentazione, nell’atomo di Bohr le orbite hanno proprietà analoghe a quelle dei modi normali delle corde vibranti: esse sono stazionarie e quantizzate. Come mostrato in figura 10, si ritrova la stessa relazione di quantizzazione nella quale l/λ è multiplo di ½, tramite un fattore n come numero quantico e con l che ora rappresenta la circonferenza dell’orbita.
Orbitali elettronici
Un descrizione quantitativa ed esauriente del moto dei pianeti necessita un’equazione del moto. Vi giunse Isaac Newton (1642-1727) con la Gravitazione Universale applicata alle conoscenze precedenti.
| ....................................................................
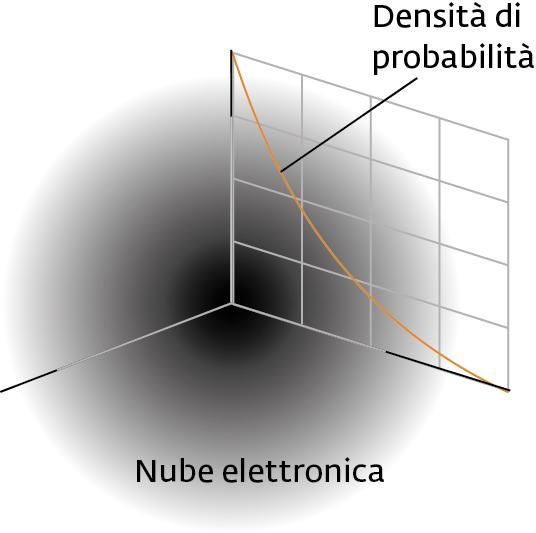
Fig. 11. La nube elettronica dell’orbitale 1s dell’atomo di Idrogeno Immagine La Chimica di Atkins - Zanichelli | ....... | ....................................... Come si è detto, nel 1924 l’ Ipotesi di de Broglie portò a rappresentare anche l’elettrone come un’onda e non solo la luce (e in generale la radiazione elettromagnetica). Nel 1927 Principio di indeterminazione del 26enne Werner Heisenberg (1901-1976) impose una descrizione probabilistica delle posizioni e quantità di moto degli elettroni negli atomi. La equazione di Schrödinger (1927) fornì infine l’equazione che descrive il comportamento di particelle non relativistiche, quali sono gli elettroni atomici. Erwin Schrödinger (1887-1931) aveva 40 anni di età. L’equazione di Schrödinger fu per l’atomo quello che la Gravitazione Universale fu per il sistema solare. Si passò dalle “orbite quantizzate” degli elettroni nell’atomo “alla Bohr” agli “ orbitali elettronici ” (pure quantizzati) nell’atomo “alla Schrödinger”. Con essi, si ottenne una descrizione completa degli stati quantici possibili per gli elettroni atomici. |
Oltre che dal numero quantico principale n già trovato con l’atomo di Bohr, gli orbitali elettronici sono contraddistinti dal “numero quantico orbitale o azimutale” l (con valori possibili eguali a 0, 1, 2, … ma al massimo n-1) e dal “numero quantico magnetico” m l (con per valori possibili i numeri interi che vanno da -l a +l.
La natura degli orbitali elettronici è stata esposta all’inizio del percorso che abbiamo qui seguito. Le posizioni in cui si può trovare un elettrone atomico sono descritte da una distribuzione di densità di probabilità, che nello spazio può essere rappresentata da una “nube elettronica”. La figura 11 mostra il risultato di calcoli teorici che danno la nube elettronica corrispondente all’orbitale detto “1s” dell’atomo di Idrogeno. Questo è l’orbitale a energia più bassa (n = 1, da cui "1") e con l = 0, il che lo rende spazialmente simmetrico (da cui la denominazione “s”).
Abbiamo dovuto giungere a nostri giorni per avere la prima immagine di un orbitale elettronico, mostrata in figura 2.
Natura facit saltus
" Natura non facit saltus " (la natura non fa salti) è una locuzione latina. Essa deriva dal principio, di remota origine, che in Natura la gradualità impera.
| ......................................................................................................
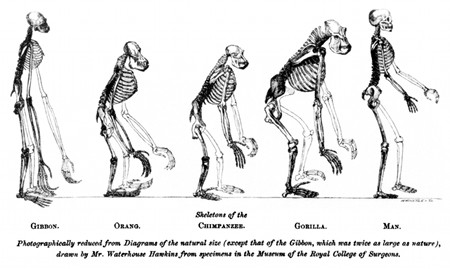
Fig. 12. L’evoluzione dell’uomo dalla scimmia
Illustrazione da T.H. Huxley, Evidence as to Man's Place in Nature (1863) Immagine Wikipedia | ....... | ....................................... Natura facit saltus " Natura non facit saltus " (la natura non fa salti) è una locuzione latina. Essa deriva dal principio, di remota origine, che in Natura la gradualità impera. La sentenza è citata in Philosophia botanica (1751, cap. 27) di Carl Linneus (1707-78), autore della fondamentale classificazione dei Regna tria naturae (animale, vegetale e minerale) ricordata in Protone, pione & adroni . Essa è implicita nell’opera di Charles Darwin (1809-82) sulla Origine della specie (1859) per evoluzione in seguito a selezione naturale, che la figura 12 mostra riferita alla specie umana dal suo stretto seguace Thomas Huxley in base a vicinanze anatomiche tra uomo e scimme. |
Nella forma “Tout va par degrés dans la nature, et rien par saut” (tutto va per gradi nella natura, e niente con salto) la sentenza è presente nell’opera Nouveaux essais (IV, 16, 12) pubblicata da Gottfried von Leibniz (1646-1716) nel 1704. Egli e Isaac Newton (1646-1727) fondarono il “ Calcolo infinitesimale ”, con le note (almeno di fama) “derivate” e gli ugualmente noti “integrali”. Coerentemente con il principio di gradualità, tale calcolo è basato sull'assioma che ogni grandezza fisica può assumere valori appartenenti a un continuum e quindi ammette variazioni di entità piccolissima o addirittura idealmente tendente a zero (in linguaggio matematico "infinitesima"). in particolare, il calcolo infinitesimale permise accuratissimi calcoli delle orbite dei corpi celesti. Come conseguenza del suddetto assioma, le orbite anche matematicamente possibili appartengono a un continuum.
Le orbite degli elettroni nell’atomo "alla Bohr" e gli orbitali nell’atomo “alla Schrödinger” non ammettono l'appartenenza a un continuum, ma piuttosto a un insieme di stati discreti caratterizzati da "numeri quantici". Nel mondo microscopico il principio di gradualità è sovvertito e la Fisica Quantistica mostra il suo temperamento rivoluzionario, tuttora vivo: Natura facit saltus.
| .................................................................................
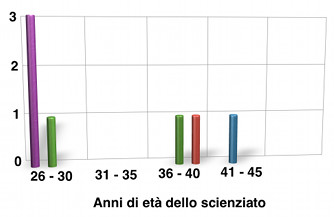
Fig. 13. Le età degli scienziati al tempo del loro contributo
| ....... | ....................................... Abbiamo sistematicamente specificato l'età che gli scienziati avevano al tempo del loro contributo alla fondazione della Fisica Quantistica, a partire dall'inizio del Novecento. La figura 13 ne mostra la distribuzione in un istogramma. Più della metà degli scienziati citati era tra i 26 e i 28 anni. La rivoluzione portata dalla Fisica Quantistica fu quasi una rivoluzione studentesca. Passando al generale, sono età in cui alle abitudini mentali non è stato ancora dato tempo materiale per tentare di assopire o erodere la libertà creativa verso il nuovo, generando pregiudizi che fossilizzano in verità assolute progressi concettuali raggiunti nel passato tramite la stessa libertà. |
Concludendo
Abbiamo constatato che le linee di Fraunhofer sono alle origini di straordinari sviluppi in vari domini della Scienza e in particolare in Fisica, Chimica, Astrofisica e Cosmologia. Ne abbiamo tratto ispirazione e motivo per delineare alcuni di essi in Da linee di Fraunhofer a Universo in espansione e in quest’articolo. A loro volta, dagli sviluppi scientifici sono nate e continuano a crescere Tecnologie e applicazioni pratiche ormai integrate nella vita umana, anche in suoi aspetti essenziali.
Collegamenti
Peter Atkins e Loretta Jones, Dall’atomo alle soluzioni , La Chimica di Atkins, Ed. Zanichelli Scuola
La fisica moderna , Sapere.it
Ray F. Egerton, Optical spectroscopy and Bohr’s model of the atom , Portland State University
Unità didattica di Storia della Spettroscopia – Università di Bari, Storia della Spettroscopia
James Schombert, Microscopic World , 21st Century Science , University of Oregon
Clara Guadagni e Paolo Strolin
.
Professore Emerito di Fisica Sperimentale
Università di Napoli "Federico II"
Complesso Univ. Monte S. Angelo
Via Cintia - 80126 Napoli - Italy
Ultima Modifica 9 Anni 2 Mesi fa da Paolo.
Si prega Accesso a partecipare alla conversazione.
Tempo creazione pagina: 0.566 secondi