Il Vuoto quantistico
- P. Strolin
-
Autore della discussione
- Offline
- Premium Utente
-
Less
Di più
11 Anni 4 Giorni fa - 8 Anni 11 Mesi fa #160
da P. Strolin
Il Mondo è pieno di Vuoto illustra come, innestandosi sul dibattito filosofico nell’antica Grecia, la fisica sperimentale classica ha dato al Vuoto un pieno diritto di esistenza. Esso mostra inoltre come dalla staticità della visione aristotelica di un Cielo con “stelle fisse” incastonate in sfere di cristallo si è giunti a un Universo costituito essenzialmente da spazio vuoto, in espansione e sede d’immani fenomeni cosmici.
L’enigma dell’interazione a distanza e i “quanti” – propedeutico a questo – introduce la “Elettro-Dinamica Quantistica” (QED), la teoria quantistica-relativistica che descrive il comportamento elettromagnetico delle particelle elementari. Con la QED fu sviluppata una nuova metodologia grafica-matematica, basata sui cosiddetti “diagrammi di Feynman”.
Il suddetto articolo mostra che le teorie quantistiche superano il concetto di trasmissione delle forze “a distanza” nel Vuoto, nato con la Gravitazione Universale di Newton attraverso un’astrazione fisica-matematica.
Vedremo qui che con la fisica quantistica il Vuoto si è anche animato, da spazio inerte che era. E’ quello che Jackson Pollock ha teso a fare con i dipinti: dare loro vita propria.
Nel complesso dei tre articoli, prendiamo coscienza di una radicale rivoluzione del pensiero filosofico e scientifico.
Jackson Pollock: il dipinto ha una vita propria
Dice Jackson Pollock (1912-56) in My painting - La mia pittura, pubblicato nell’anno della sua tragica e precoce morte per incidente stradale:
.............................................
L’atto creativo dell’artista per fare “emergere la vita propria” del dipinto è detto “action painting” (figura 1). Non è basato su un programmatico disegno come nella pittura classica. L’artista vive in diretta lo svolgersi della creazione, interagendo continuamente con l’opera che si sta formando: un semplice dare e prendere. Egli agisce versando direttamente il colore (“dripping”, sgocciolatura) e utilizzando strumenti rudimentali.
I protagonisti della rivoluzione artistica nel cui ambito si situa l’opera di Jackson Pollock furono gli artisti della Scuola di New York, detti gli “ Irascibili ” per la famosa protesta contro il Metropolitan Museum of Art di New York allorché nel 1950 furono esclusi da una mostra sull’arte contemporanea americana. La figura 2 li mostra ironicamente ritratti in abiti alto-borghesi. Jackson Pollock è al centro. Insieme a lui sono Willem de Kooning , Mark Rothko e altri artisti, che nella seconda metà degli anni Trenta avevano iniziato a parlare un nuovo linguaggio figurativo detto “ Espressionismo Astratto ”.
Una breve sintesi
I nostri primi passi consisteranno nel seguire la rappresentazione teorica dei livelli energetici dell’elettrone nell’atomo di Idrogeno, dall’atomo secondo Bohr alla struttura atomica a “orbitali” conseguente all’equazione quantistica-ondulatoria con cui Schrödinger descrisse il comportamento dell’elettrone. Vedremo poi le correzioni apportate ai livelli energetici dalla descrizione relativistica dell’elettrone data dall’equazione di Dirac, che tiene anche conto del suo momento angolare di spin .
L’osservazione di un’apparente anomalia nei livelli energetici dell’elettrone nell’atomo di Idrogeno (lo “spostamento di Lamb”) indusse lo sviluppo della QED, teoria che estende il dominio di validità dell'equazione di Dirac. La vedremo a un livello più avanzato che in L’enigma dell’interazione a distanza e i “quanti” .
Dopo di questo potremo offrirci la soddisfazione di capire, almeno qualitativamente, come la visione quantistica-relativistica del Vuoto data dalla QED ha animato il Vuoto. Vedremo poi come il bosone di Higgs introduce una nuova rivoluzione, più difficilmente comprensibile dai “non addetti ai lavori”.
Nel corso di questo cammino, avremo l’occasione di rivisitare “con gli occhi del Vuoto” argomenti trattati in altri articoli, che richiameremo di volta in volta.
L’atomo secondo Bohr e Schrödinger
Da linee di Fraunhofer a Universo in espansione e Da linee di Fraunhofer ad atomo quantistico già mostrano la ricca messe scientifica portata dalla scoperta dei livelli energetici "quantizzati" degli elettroni atomici. In particolare, il secondo articolo illustra l’atomo secondo la visione concepita da Niels Bohr nel 1913.
Nel 1927 l’ equazione di Schrödinger fornì una descrizione quantistica-ondulatoria degli elettroni e condusse a rappresentare gli stati degli elettroni atomici in termini di “ orbitali ”. A ogni orbitale corrisponde una distribuzione di probabilità (comunemente detta “nube elettronica”) della posizione dell’elettrone attorno al nucleo.
L’equazione di Schrödinger permette un calcolo analitico formalmente esatto degli orbitali dell’atomo di Idrogeno, che possiede un solo elettrone. Gli orbitali sono definiti da “numero quantico principale” n, “numero quantico di momento angolare orbitale” l e “numero quantico magnetico” m. Il numero quantico magnetico m corrisponde alla proiezione di quello orbitale l in una direzione prescelta (quella del campo magnetico se esso è presente). In assenza di campo magnetico, l’energia dello stato quantico dipende esclusivamente da n. Un campo magnetico separa energeticamente stati con diverso m.
La figura 3 mostra le nubi elettroniche corrispondenti agli orbitali dell’atomo di Idrogeno con l = 0 (indicati come S) e l = 1 (indicati come P), per n = 1 e 2.
L’atomo secondo Dirac
L’ equazione di Dirac perfeziona la descrizione degli orbitali considerando gli effetti relativistici e lo “spin” dell’elettrone, di cui trattano in particolare Lo spin e Lo spin dell’elettrone: roba da ragazzi in una serie di articoli sullo spin tra i Saggi tematici . Viene introdotto il “numero quantico di momento angolare totale” j, il quale è un’opportuna combinazione di quello “orbitale” (di cui sopra) e di quello corrispondente allo spin. Ai livelli energetici dati dal “numero quantico principale” n si apportano piccole correzioni dette di “struttura fine” (dell’ordine di 1%), che dipendono unicamente da j. Non è prevista alcuna dipendenza dal “numero quantico di momento angolare orbitale” l. Rinviamo all’Appendice 1 per approfondimenti.
Qualcosa accade nel Vuoto
Nella lezione Nobel 1955 di Willis Lamb (1913-2008) leggiamo:
Secondo l’usuale denominazione spettroscopica, gli stati 2S ½ e 2P ½ dell’atomo di Idrogeno menzionati da Lamb sono caratterizzati dagli stessi numeri quantici n = 2 e j = ½. Quanto detto precedentemente spiega la previsione della teoria di Dirac menzionata da Lamb che essi debbano avere livelli energetici esattamente coincidenti.
Ebbene, nel 1947 Willis Lamb (figura 4) – all’età di 34 anni e assieme al suo studente Robert Retherford – scoprì con un raffinato esperimento che tra i livelli energetici dei due stati esiste una piccolissima differenza: circa 4 milionesimi di eV (figura 5), dell’ordine di un milione di volte meno dei circa 10 eV che separano i livelli degli orbitali con n = 1 e n = 2. Essa va sotto il nome di “spostamento di Lamb”. A cosa può collegarsi questo effetto?
I due stati differiscono solo nel numero quantico orbitale l, rispettivamente l = 0 e l = 1 come indicato da S e P nelle rispettive denominazioni. In fisica classica il momento angolare L aumenta con il raggio dell’orbita r secondo la relazione L = mr v, ove m e v sono la massa e la velocità. Corrispondentemente, nella descrizione quantistica dell’atomo a un maggior valore del numero quantico di momento angolare orbitale l è associata una maggiore estensione della “nube elettronica”. In particolare nello stato P (l = 1) l’elettrone è mediamente più distante dal protone di quanto non lo sia nello stato S (l = 0), come mostrato figura 3.
Si trae la conclusione che lo spostamento di Lamb è collegato al maggiore spazio mediamente esistente tra protone ed elettrone. Lo spazio stesso (nominalmente vuoto) influisce sulla loro interazione: qualcosa succede nel cosiddetto “Vuoto”!
Lo spostamento di Lamb fu la piccolissima scintilla che innescò il fuoco dello sviluppo della QED e rivoluzionò il concetto di Vuoto. Willis Lamb fu insignito del Premio Nobel 1955 . Per maggiori dettagli, vedete Landmarks: Lamb shift verifies new quantum concept dell’American Physical Society o la summenzionata lezione Nobel.
Attualizzando il discorso nel linguaggio dei diagrammi di Feynman, fu necessario andare oltre la rappresentazione dell’interazione degli elettroni mediata da un semplice “ fotone ”, presentata in L’enigma dell’interazione a distanza e i “quanti” .
In termini di diagrammi di Feynman, l’interazione mediata da un fotone corrisponde all’equazione di Dirac. Mostreremo gli effetti più sottili che furono individuati e il loro impatto sul concetto di Vuoto.
Interazione elettrone-elettrone mediata da un fotone
Iniziamo riassumendo dal suddetto articolo la rappresentazione dell'interazione elettromagnetica quantistica-relativistica tra due elettroni mediata da un fotone, secondo il diagramma di Feynman in figura 6 a sinistra.
Secondo questo diagramma, l’interazione avviene attraverso la trasmissione di un fotone γ da un “vertice” di emissione a uno di assorbimento. Il fotone ha funzione di “mediatore” ed è detto “virtuale” poiché resta interamente confinato all’interno del processo.
Alla trasmissione del fotone mediatore da un vertice all’altro è associato un fattore (detto “propagatore”) nella “ampiezza di probabilità” (definita in Onde e particelle per pedoni molto curiosi ) che il processo avvenga. Esso si riflette sul fattore 1 / r 2 che compare nella legge coulombiana dell'interazione elettrostatica.
A ogni vertice di emissione o assorbimento di un fotone virtuale si associa un fattore che ne rappresenta il contributo all’ampiezza di probabilità, detto “costante di accoppiamento”. Questa caratterizza il tipo d’interazione e (per quelle elettromagnetiche) si riflette sul valore della "costante di Coulomb" k che appare nella legge d’interazione elettrostatica.
......
Creazione e annichilazione di coppie elettrone-positrone
Secondo la relazione einsteiniana E = mc 2 , l’energia si può convertire in materia e viceversa. L’energia di un fotone può essere così convertita in un elettrone e- accompagnato dalla sua antiparticella, un positrone e + . Per essere precisi, notiamo che questo processo avviene allorchè il fotone attraversa uno strato di materia e interagisce con i nuclei atomici in essa contenuti.
La figura 7 mostra due esempi di questo processo di “creazione di coppia” in un dettaglio di un famosa interazione di neutrino, registrata al CERN in una camera a bolle ” e discussa in Interazione Elettrodebole . I fotoni (elettricamente neutri) non sono visti e nello schema in basso sono indicati da linee tratteggiate. L’elettrone e il positrone si dipartono da essi a V e sono caratterizzati da tracce curvate in senso opposto da un campo magnetico, in virtù dell’opposto valore della loro carica elettrica.
La relazione einsteiniana massa-energia permette anche il processo inverso: la “annichilazione” di una coppia elettrone-positrone in un fotone. I due processi sono rappresentati “alla Feynman” in figura 8. Si noti che nei diagrammi di Feynman le antiparticelle (un positrone e + in figura) sono caratterizzate da una freccia in senso opposto rispetto a quella delle particelle: questa è una convenzione giustificata da considerazioni di fisica.
Una coppia virtuale nascosta nel mediatore
Continuiamo a ragionare per avanzare nella “costruzione” di una visione dell’interazione elettrone-elettrone tramite i diagrammi di Feynman secondo la QED. Come in L’enigma dell’interazione a distanza e i “quanti” , ci limiteremo a considerarli come strumento grafico e a livello qualitativo.
Conversione e annichilazione si possono susseguire anche per il fotone virtuale, secondo il diagramma di Feynman in figura 6 a destra. Con l’energia del fotone virtuale è creata una coppia (virtuale) elettrone-positrone, che è necessariamente riconvertita in un fotone all’interno del processo. In tal modo, la catena fotone-coppia-fotone resta virtuale e confinata all’interno del processo. Nel suo complesso, essa ha funzioni di mediatore.
Come detto precedentemente, nell’espressione dell'ampiezza di probabilità complessiva a ciascuno dei vertici di emissione e assorbimento del fotone virtuale (presenti in ambedue i diagrammi figura 6) va associato un fattore pari alla costante di accoppiamento. A esso corrisponde una probabilità notevolmente minore di 1. Il diagramma in figura 6 a destra presenta due vertici in più (quelli di creazione e annichilazione della coppia elettrone-positrone), a ciascuno dei quali va associato lo stesso fattore di cui sopra, Quindi tale diagramma risulta doppiamente sfavorito in termini di ampiezza di probabilità.
Ne consegue che il diagramma con coppia virtuale elettrone-positrone porta una piccola correzione (dell’ordine del %) alla probabilità che il processo avvenga unicamente in base al diagramma con il solo fotone.
Diagrammi di Feynman e approssimazioni successive
Secondo la precisione che si vuole raggiungere nella descrizione quantitativa di un processo (l’interazione elettrone-elettrone nel caso di cui sopra), si procede per approssimazioni successive considerando diagrammi progressivamente più complessi e con un maggior numero di vertici. Conseguentemente il loro contributo è via via decrescente. La figura mostra i primi due diagrammi che descrivono l'interazione elettrone-elettrone.
La rappresentazione del fenomeno è data dal complesso dei diagrammi di Feynman considerati. Matematicamente, le corrispondenti ampiezze di probabilità vanno addizionate secondo i dettami della fisica quantistica. Il loro valore progressivamente più basso assicura che esse costituiscano solamente piccole correzioni.
Non ci si stupisca se, traducendo i diagrammi in espressioni matematiche secondo le regole di Feynman, la legge fisica è rappresentata da una somma di espressioni invece che da una singola come per esempio nella legge d’interazione elettrostatica. Chi ha ordinato che una legge fisica debba essere rappresentata da una singola espressione matematica e non da una somma?
Con la suddetta metodologia, la QED ha raggiunto precisioni straordinarie nella descrizione dei fenomeni. Tramite confronto con dati sperimentali di paragonabile precisione, la sua validità è stata verificata con una accuratezza fino all’ordine di grandezza di parti per milione come detto in Interazioni elettromagnetiche “alla Feynman” .
Polarizzazione del Vuoto
La formazione di una coppia virtuale elettrone-positrone entro un fotone virtuale va sotto il nome di “polarizzazione del Vuoto”. La parola viene dal fatto che si creano contemporaneamente due specie di poli opposti (elettrone e positrone, e in generale particella-antiparticella), inseparabili come i poli Nord e Sud di una calamita.
Le coppie particella-antiparticella formatesi nel Vuoto sono come “bollicine” quantistiche-relativistiche, aventi vita temporanea. La QED trasforma la visione del Vuoto da spazio inerte a vivo.
Questo effetto evoca, infatti, l’immagine delle bollicine nello spumante versato nei nostri bicchieri da una bottiglia appena aperta (figura 9). All’apertura della bottiglia la pressione esterna cala improvvisamente e mette il gas disciolto nella massa del liquido in “fuori gioco” ossia, detto con parole scientifiche, in condizioni di sovra-saturazione rispetto alla Legge di Henry (1803). Al gas non resta che uscirne formando bollicine.
Il vuoto atomico si anima
La figura 10, tratta dal famoso libro divulgativo di Richard Feynman dal titolo QED: la strana teoria della luce e della materia (Princeton University Press - Adelphi, 1985), sintetizza – in un’immagine che non è un diagramma di Feynman - la visione che la QED ispira per l’interazione tra protone e elettrone nell’atomo di Idrogeno. Fotoni virtuali sono continuamente emessi e riassorbiti, e danno eventualmente luogo a “bollicine” particella-antiparticella. Il vuoto atomico è “virtualmente” animato.
Chi è Mr. Electron?
La QED porta anche a una nuova descrizione quantistica-relativistica di particella elementare, che ci mette di fronte a interrogativi fondamentali ma complessi. Ne daremo un accenno.
Secondo la QED, un processo è rappresentato dall’insieme dei diagrammi di Feynman che sono necessari per raggiungere la precisione voluta, via via più complessi e a livelli di probabilità più basso.
Anche una particella come l’elettrone è rappresentata da un complesso di diagrammi di Feynman. La figura 11 ne mostra alcuni. A sinistra è mostrato il diagramma più elementare, corrispondente al cosiddetto “elettrone nudo”. Nel diagramma al centro un fotone virtuale è emesso e riassorbito. Quello a destra mostra che esso può generare una coppia virtuale particella-antiparticella (in figura elettrone-positrone). In sostanza, l’elettrone nudo viaggia con il “rivestimento” previsto da altri diagrammi. Non solo il Vuoto non è vuoto, ma il confine tra pieno e vuoto non è netto.
Notate che questo effetto non ha nulla a che vedere con l’indeterminazione nella posizione dell’elettrone conseguente al “ Principio di Indeterminazione ”, già implicita nelle equazioni di Schrödinger e di Dirac.
Se siete curiosi, vedete in Appendice 2 come rispondere alla domanda: quale è la carica dell'elettrone?
Maja e fisica quantistica
La rappresentazione dell’elettrone con una serie di diagrammi ripropone un interrogativo sul significato fisico della presenza di più di un solo diagramma. Rispondiamo ricorrendo alla Maja di Francisco Goya (1746-1828) come termine di paragone in fisica classica. La figure 12 mostra i suoi famosi dipinti Maja desnuda e Maja vestida. A ogni determinato istante, Maja è “o nuda o vestita”.
A un oggetto quantistico come l’elettrone succede qualcosa di completamente diverso, che non ha corrispondenti alla scala macroscopica ma va ugualmente accettato come realtà fisica. La scala microscopica della fisica quantistica richiede infatti un nuovo modo di pensare i fenomeni, come discusso in Pensare in Quantistico . L’elettrone può essere trovato in uno stato ("nudo" o "vestito") rappresentato da “uno qualsiasi” dei diagrammi di Feynman in figura 11, o da altri più complessi non mostrati. Ad ogni diagramma è semplicemente associata un (ampiezza di) probabilità. L’elettrone è rappresentato dal complesso dei diagrammi.
QED e spostamento di Lamb
I fotoni virtuali riassorbiti dalla loro sorgente (come quello nel diagramma centrale in figura 11) e le coppie virtuali elettrone-positrone (come nel diagramma a destra in figura 6) costituiscono esempi di circuiti che si chiudono su se stessi e non escono nel mondo esterno. Tuttavia, essi riflettono sulle previsioni fornite dalla QED. In particolare, l'aggiunta di diagrammi di Feynman influisce sulla determinazione dei livelli energetici degli elettroni atomici e porta a delle piccole correzioni che spiegano lo spostamento di Lamb rispetto ai livelli attesi in base al solo diagramma più elementare.
Fotoni virtuali in circuito chiuso con l'aggiunta di una bollicina (come nel diagramma a destra in figura 11) portano a piccole correzioni di piccole correzioni e quindi i loro effetti sono solitamente trascurabili. Questo è detto nel caso che siate stati tanto attenti da porvi la domanda.
Il bosone di Higgs e l’energia del Vuoto
Simmetrie e Interazioni Fondamentali espone come le Interazioni Fondamentali sono oggi formulate imponendo il rispetto di simmetrie dette “di Gauge”. Il bosone di Higgs: una rivoluzione rispetto al comune pensare e Rottura Spontanea della Simmetria e bosone di Higgs mostrano come si è giunti a predire l’esistenza del bosone di Higgs, ingrediente fondamentale per riprodurre nella teoria il fatto che le particelle possono avere massa non nulla.
Il concetto di Vuoto vede una nuova rivoluzione: il cosiddetto Vuoto pullula di bosoni di Higgs. Il fatto singolarmente nuovo è che al loro stato energetico più basso (quello che in fisica classica è lo stato di quiete) non corrisponde un’energia nulla. Quindi i bosoni di Higgs danno al Vuoto energia propria. Siamo passati da un Vuoto letteralmente vuoto a un Vuoto animato, e infine a un Vuoto con energia propria!
Le masse delle particelle note derivano dall'interazione con bosoni di Higgs secondo un quadro teorico coerente, ma al momento non appare nessun collegamento speciale tra esse, nessuna struttura all'interno della quale sia possibile riempire di significato i loro diversi valori. Il Vuoto ha ancora cose da dire sulle masse delle particelle e sulla sua stessa natura!
Dare e prendere
Jackson Pollock con il suo “action painting” interagiva con la sua opera, facendone “emergere la vita propria” in un continuo “dare e prendere”. La figura 13 mostra un dipinto di Pollock. Solo dal vero se ne riceve il pieno impatto espressivo. Vedetene anche un dettaglio . Il titolo stesso “Number 8” manifesta che esso non è ammaestrato a dire qualcosa, ma parla liberamente il suo linguaggio avendo “vita propria”.
La Scienza segue un simile processo creativo, procedendo attraverso un continuo interagire con la Natura: vede, interroga sperimentalmente, vede, riflette, interroga e così via. Così stanno emergendo le proprietà del Vuoto e la sua “vita propria”.
Che cosa ci porta questa conoscenza? In Il Mondo è pieno di Vuoto abbiamo visto che la natura del Vuoto fu indagata già nella Filosofia dell'antica Grecia in relazione alla teoria atomistica. Forse anche allora c'era chi si poneva la stessa domanda. La risposta è venuta dalla Storia: lo sviluppo della nostra civiltà non sarebbe stato lo stesso senza l'impulso dato dal pensiero scientifico e filosofico greco. Anche oggi bisogna guardare avanti e pensare che la vera risposta verrà dalla Storia: quella ancora da scrivere.
Riferimenti bibliografici
Richard P. Feynman, La legge fisica (Modern Library – Bollati Boringhieri, 1965)
Richard P. Feynman, QED: the strange theory of light and matter - QED: la strana teoria della luce e della materia , Editore Princeton University Press (1965) - Adelphi (1989)
Quantum Electrodinamics (QED) , Cronodon
Robert Matthews, Nothing like a vacuum : what could be a permanent, decidedly nonzero source of energy in the Universe, with cosmic consequences? The vacuum is far from empty , New Scientist, (1995)
APPENDICE 1: L’atomo secondo Dirac
La Teoria della Relatività Speciale fu formulata nel 1905 e stabilì l’ equivalenza massa-energia secondo E = mc 2 .
Nel 1928 Paul A. M. Dirac (1902-84) con la sua magica equazione fornì una descrizione quantistica-ondulatoria dell’elettrone valida anche in regime relativistico (contrariamente all'equazione di Schrödinger), inoltre, comprensiva del suo “ momento angolare di spin ”. L’equazione di Dirac vale per tutte le particelle elementari con “numero quantico di spin” s=½, dette “ fermioni ”.
Di più, l’equazione di Dirac predisse la “necessaria” esistenza di anti-particelle. Nel 1932, ne fu scoperta la prima: l’anti-elettrone, comunemente detto “positrone” e indicato con il simbolo e + lasciando e- per l’elettrone.
Nella descrizione degli orbitali atomici dell’atomo di Idrogeno secondo l’equazione di Dirac, il “numero quantico di momento angolare totale” j è dato da un’opportuna combinazione di quello orbitale l e di quello di spin. Nell’usuale denominazione degli stati quantici, il valore di l è indicato da una lettera maiuscola S, P, … per l = 0, 1, … e gli stati con l = 0 e l = 1 sono rispettivamente denotati da nS j e nP j .
L’applicazione dell’equazione di Dirac porta a delle piccole correzioni (dell’ordine di 1%) ai livelli energetici degli elettroni atomici, dette di “ struttura fine ”. Esse derivano da effetti relativistici e dalla presenza sia di un momento angolare orbitale che di spin. In assenza di campo magnetico, i livelli energetici dipendono da n con una correzione di struttura fine funzione di j e non di l. Ne consegue che i livelli energetici di stati con gli stessi valori di n e di j sono identici (nel linguaggio scientifico “degeneri”) anche se caratterizzati da diversi valori del momento angolare orbitale, cioè di l.
Facciamo l’esempio pertinente allo spostamento di Lamb. Si ha lo stesso j = ½ da uno stato S (l = 0) con j = 0 + ½ e da uno stato P (l=1) con j = 1 - ½ , ove il secondo dei due termini proviene dal momento angolare di spin e (per lo stato P) dipende dal suo orientamento rispetto a quello orbitale. Nel caso n = 2 questi stati S e P sono rispettivamente denotati come 2S ½ e 2P ½ . I corrispondenti livelli energetici sono rigorosamente identici.
APPENDICE 2: Quale è la carica dell'elettrone?
La figura 14 traspone il complesso di diagrammi che rappresentano l'elettrone (ai cui primi si riferisce la figura 9) in un’immagine che – al pari di quella in figura 10 – è ispirata alla QED senza avere il significato grafico-matematico dei diagrammi di Feynman. L’elettrone nudo è rivestito da coppie virtuali particella-antiparticella e “tutto accade come se" le (anti) particelle con carica elettrica positiva fossero attratte verso l’elettrone (con carica negativa) e tendessero a neutralizzarne parzialmente la carica elettrica negativa.
Sorge un interrogativo fondamentale: a cosa corrisponde la “carica dell’elettrone” che troviamo sui libri di fisica classica? Non può essere che la carica vista a distanza macroscopica e quindi con quella dell’elettrone completamente “rivestito”.
Incalziamo con un’altra domanda. Come confermare sperimentalmente questa visione? Se essa è corretta, la carica dell’elettrone sperimentalmente misurata non ha un valore univoco: una particella di alta energia che penetri entro il “rivestimento” che neutralizza parzialmente l’elettrone nudo e gli si avvicini dovrebbe sperimentare un valore della carica dell’elettrone maggiore di quella della fisica classica. Questo effetto è stato riscontrato facendo collidere elettroni e positroni ad alta energia.
Immaginando di far collidere elettroni e positroni a energia sempre più alta, noterete con una certa apprensione che la carica apparente dell'elettrone aumenta sempre di più.
L'elettrone nudo è sperimentalmente inavvicinabile, altrimenti così continuando (teoricamente) troveremmo per esso una carica apparente addirittura infinita. Il serio problema che si pone è fortunatamente solo teorico, perché dal punto di vista sperimentale vi è un'ancora certa: il valore della carica dell'elettrone nella fisica classica, misurato a distanza macroscopica e solitamente indicato con il simbolo e.
Ma allora che fare della problematica carica infinita dell'inavvicinabile elettrone assolutamente nudo? La risposta teorica a questo interrogativo teorico è da "uovo di Colombo": ancoriamo anche la teoria al solo valore misurato e. La suddetta carica infinita perde drammaticità pratica e viene ridimensionata (in linguaggio tecnico "rinormalizzata") riassorbendola all'interno stesso della teoria. Questa è in sintesi la complessa procedura detta di “rinormalizzazione".
Professore Emerito di Fisica Sperimentale
Università di Napoli "Federico II"
Complesso Univ. Monte S. Angelo
Via Cintia - 80126 Napoli - Italy
Il Vuoto quantistico è stato creato da P. Strolin
Il Vuoto quantistico
................
................
Per domande: autori o
Domanda a un esperto
................Il Mondo è pieno di Vuoto illustra come, innestandosi sul dibattito filosofico nell’antica Grecia, la fisica sperimentale classica ha dato al Vuoto un pieno diritto di esistenza. Esso mostra inoltre come dalla staticità della visione aristotelica di un Cielo con “stelle fisse” incastonate in sfere di cristallo si è giunti a un Universo costituito essenzialmente da spazio vuoto, in espansione e sede d’immani fenomeni cosmici.
L’enigma dell’interazione a distanza e i “quanti” – propedeutico a questo – introduce la “Elettro-Dinamica Quantistica” (QED), la teoria quantistica-relativistica che descrive il comportamento elettromagnetico delle particelle elementari. Con la QED fu sviluppata una nuova metodologia grafica-matematica, basata sui cosiddetti “diagrammi di Feynman”.
Il suddetto articolo mostra che le teorie quantistiche superano il concetto di trasmissione delle forze “a distanza” nel Vuoto, nato con la Gravitazione Universale di Newton attraverso un’astrazione fisica-matematica.
Vedremo qui che con la fisica quantistica il Vuoto si è anche animato, da spazio inerte che era. E’ quello che Jackson Pollock ha teso a fare con i dipinti: dare loro vita propria.
Nel complesso dei tre articoli, prendiamo coscienza di una radicale rivoluzione del pensiero filosofico e scientifico.
| .............................................
Fig. 1. La pittura di azione di Jackson Pollock
Fotografia di Hans Namuth (1950) Immagine Juliet Art Magazine | ... | ......................
Fig. 2. Il gruppo irascibile di artisti di avanguardia che ha dato battaglia
alla Mostra in una fotografia di Nina Leen, (Life, 15 gennaio1951) Immagine International Center of Photography |
Jackson Pollock: il dipinto ha una vita propria
Dice Jackson Pollock (1912-56) in My painting - La mia pittura, pubblicato nell’anno della sua tragica e precoce morte per incidente stradale:
.............................................
“The painting has a life of its own. I try to let it come through. It is only when I lose contact with the painting that the result is a mess. Otherwise there is pure harmony, an easy give and take”
Il dipinto ha una vita propria. Io cerco di farla emergere. Il risultato appare disordinato solo quando perdo contatto con il dipinto; altrimenti c’è pura armonia, un semplice dare e prendere.
L’atto creativo dell’artista per fare “emergere la vita propria” del dipinto è detto “action painting” (figura 1). Non è basato su un programmatico disegno come nella pittura classica. L’artista vive in diretta lo svolgersi della creazione, interagendo continuamente con l’opera che si sta formando: un semplice dare e prendere. Egli agisce versando direttamente il colore (“dripping”, sgocciolatura) e utilizzando strumenti rudimentali.
I protagonisti della rivoluzione artistica nel cui ambito si situa l’opera di Jackson Pollock furono gli artisti della Scuola di New York, detti gli “ Irascibili ” per la famosa protesta contro il Metropolitan Museum of Art di New York allorché nel 1950 furono esclusi da una mostra sull’arte contemporanea americana. La figura 2 li mostra ironicamente ritratti in abiti alto-borghesi. Jackson Pollock è al centro. Insieme a lui sono Willem de Kooning , Mark Rothko e altri artisti, che nella seconda metà degli anni Trenta avevano iniziato a parlare un nuovo linguaggio figurativo detto “ Espressionismo Astratto ”.
Una breve sintesi
I nostri primi passi consisteranno nel seguire la rappresentazione teorica dei livelli energetici dell’elettrone nell’atomo di Idrogeno, dall’atomo secondo Bohr alla struttura atomica a “orbitali” conseguente all’equazione quantistica-ondulatoria con cui Schrödinger descrisse il comportamento dell’elettrone. Vedremo poi le correzioni apportate ai livelli energetici dalla descrizione relativistica dell’elettrone data dall’equazione di Dirac, che tiene anche conto del suo momento angolare di spin .
L’osservazione di un’apparente anomalia nei livelli energetici dell’elettrone nell’atomo di Idrogeno (lo “spostamento di Lamb”) indusse lo sviluppo della QED, teoria che estende il dominio di validità dell'equazione di Dirac. La vedremo a un livello più avanzato che in L’enigma dell’interazione a distanza e i “quanti” .
Dopo di questo potremo offrirci la soddisfazione di capire, almeno qualitativamente, come la visione quantistica-relativistica del Vuoto data dalla QED ha animato il Vuoto. Vedremo poi come il bosone di Higgs introduce una nuova rivoluzione, più difficilmente comprensibile dai “non addetti ai lavori”.
Nel corso di questo cammino, avremo l’occasione di rivisitare “con gli occhi del Vuoto” argomenti trattati in altri articoli, che richiameremo di volta in volta.
L’atomo secondo Bohr e Schrödinger
Da linee di Fraunhofer a Universo in espansione e Da linee di Fraunhofer ad atomo quantistico già mostrano la ricca messe scientifica portata dalla scoperta dei livelli energetici "quantizzati" degli elettroni atomici. In particolare, il secondo articolo illustra l’atomo secondo la visione concepita da Niels Bohr nel 1913.
|
Fig. 3. Le nubi elettroniche corrispondenti agli orbitali S
(l = 0) e P (l = 1) dell’atomo di Idrogeno, per n = 1 e 2
Immagine tratta da
Wikipedia
|
Nel 1927 l’ equazione di Schrödinger fornì una descrizione quantistica-ondulatoria degli elettroni e condusse a rappresentare gli stati degli elettroni atomici in termini di “ orbitali ”. A ogni orbitale corrisponde una distribuzione di probabilità (comunemente detta “nube elettronica”) della posizione dell’elettrone attorno al nucleo.
L’equazione di Schrödinger permette un calcolo analitico formalmente esatto degli orbitali dell’atomo di Idrogeno, che possiede un solo elettrone. Gli orbitali sono definiti da “numero quantico principale” n, “numero quantico di momento angolare orbitale” l e “numero quantico magnetico” m. Il numero quantico magnetico m corrisponde alla proiezione di quello orbitale l in una direzione prescelta (quella del campo magnetico se esso è presente). In assenza di campo magnetico, l’energia dello stato quantico dipende esclusivamente da n. Un campo magnetico separa energeticamente stati con diverso m.
La figura 3 mostra le nubi elettroniche corrispondenti agli orbitali dell’atomo di Idrogeno con l = 0 (indicati come S) e l = 1 (indicati come P), per n = 1 e 2.
L’atomo secondo Dirac
L’ equazione di Dirac perfeziona la descrizione degli orbitali considerando gli effetti relativistici e lo “spin” dell’elettrone, di cui trattano in particolare Lo spin e Lo spin dell’elettrone: roba da ragazzi in una serie di articoli sullo spin tra i Saggi tematici . Viene introdotto il “numero quantico di momento angolare totale” j, il quale è un’opportuna combinazione di quello “orbitale” (di cui sopra) e di quello corrispondente allo spin. Ai livelli energetici dati dal “numero quantico principale” n si apportano piccole correzioni dette di “struttura fine” (dell’ordine di 1%), che dipendono unicamente da j. Non è prevista alcuna dipendenza dal “numero quantico di momento angolare orbitale” l. Rinviamo all’Appendice 1 per approfondimenti.
|
Fig. 4. Willis Lamb e il suo apparato sperimentale
Immagine Wikipedia | ... |
Fig. 5. Lo spostamento di Lamb
Immagine Gouri Goutam Borthakur |
Qualcosa accade nel Vuoto
Nella lezione Nobel 1955 di Willis Lamb (1913-2008) leggiamo:
“Dirac discovered an equation which described an electron with wave properties, charge, spin, magnetic moment and a mass depending on velocity as required by relativity theory. The energy levels of hydrogen were given by Dirac’s theory with high precision. [...] The exact coincidence in energy of the 2S
½
and 2P
½
states is a consequence of the assumed law of attraction between electron and proton. Any departure from this law would cause a separation of these levels”
Dirac scoprì un'equazione che descriveva un elettrone con proprietà ondulatorie, carica, spin, momento magnetico e una massa dipendente dalla velocità come richiesto dalla teoria della relatività . I livelli energetici dell’idrogeno erano dati dalla teoria di Dirac con alta precisione. [...] La coincidenza esatta in energia degli stati 2S ½ e 2P ½ è una conseguenza della legge assunta per descrivere l’attrazione tra elettrone e protone. Ogni deviazione da questa legge potrebbe causare una separazione di questi livelli.
Dirac scoprì un'equazione che descriveva un elettrone con proprietà ondulatorie, carica, spin, momento magnetico e una massa dipendente dalla velocità come richiesto dalla teoria della relatività . I livelli energetici dell’idrogeno erano dati dalla teoria di Dirac con alta precisione. [...] La coincidenza esatta in energia degli stati 2S ½ e 2P ½ è una conseguenza della legge assunta per descrivere l’attrazione tra elettrone e protone. Ogni deviazione da questa legge potrebbe causare una separazione di questi livelli.
Secondo l’usuale denominazione spettroscopica, gli stati 2S ½ e 2P ½ dell’atomo di Idrogeno menzionati da Lamb sono caratterizzati dagli stessi numeri quantici n = 2 e j = ½. Quanto detto precedentemente spiega la previsione della teoria di Dirac menzionata da Lamb che essi debbano avere livelli energetici esattamente coincidenti.
Ebbene, nel 1947 Willis Lamb (figura 4) – all’età di 34 anni e assieme al suo studente Robert Retherford – scoprì con un raffinato esperimento che tra i livelli energetici dei due stati esiste una piccolissima differenza: circa 4 milionesimi di eV (figura 5), dell’ordine di un milione di volte meno dei circa 10 eV che separano i livelli degli orbitali con n = 1 e n = 2. Essa va sotto il nome di “spostamento di Lamb”. A cosa può collegarsi questo effetto?
I due stati differiscono solo nel numero quantico orbitale l, rispettivamente l = 0 e l = 1 come indicato da S e P nelle rispettive denominazioni. In fisica classica il momento angolare L aumenta con il raggio dell’orbita r secondo la relazione L = mr v, ove m e v sono la massa e la velocità. Corrispondentemente, nella descrizione quantistica dell’atomo a un maggior valore del numero quantico di momento angolare orbitale l è associata una maggiore estensione della “nube elettronica”. In particolare nello stato P (l = 1) l’elettrone è mediamente più distante dal protone di quanto non lo sia nello stato S (l = 0), come mostrato figura 3.
Si trae la conclusione che lo spostamento di Lamb è collegato al maggiore spazio mediamente esistente tra protone ed elettrone. Lo spazio stesso (nominalmente vuoto) influisce sulla loro interazione: qualcosa succede nel cosiddetto “Vuoto”!
Lo spostamento di Lamb fu la piccolissima scintilla che innescò il fuoco dello sviluppo della QED e rivoluzionò il concetto di Vuoto. Willis Lamb fu insignito del Premio Nobel 1955 . Per maggiori dettagli, vedete Landmarks: Lamb shift verifies new quantum concept dell’American Physical Society o la summenzionata lezione Nobel.
Attualizzando il discorso nel linguaggio dei diagrammi di Feynman, fu necessario andare oltre la rappresentazione dell’interazione degli elettroni mediata da un semplice “ fotone ”, presentata in L’enigma dell’interazione a distanza e i “quanti” .
In termini di diagrammi di Feynman, l’interazione mediata da un fotone corrisponde all’equazione di Dirac. Mostreremo gli effetti più sottili che furono individuati e il loro impatto sul concetto di Vuoto.
Interazione elettrone-elettrone mediata da un fotone
Iniziamo riassumendo dal suddetto articolo la rappresentazione dell'interazione elettromagnetica quantistica-relativistica tra due elettroni mediata da un fotone, secondo il diagramma di Feynman in figura 6 a sinistra.
|
Fig. 6. A sinistra: interazione tra due elettroni mediata da un fotone virtuale γ
A destra: una coppia virtuale elettrone-positrone associata
a un fotone virtuale - Immagini
Cronodon
|
Secondo questo diagramma, l’interazione avviene attraverso la trasmissione di un fotone γ da un “vertice” di emissione a uno di assorbimento. Il fotone ha funzione di “mediatore” ed è detto “virtuale” poiché resta interamente confinato all’interno del processo.
Alla trasmissione del fotone mediatore da un vertice all’altro è associato un fattore (detto “propagatore”) nella “ampiezza di probabilità” (definita in Onde e particelle per pedoni molto curiosi ) che il processo avvenga. Esso si riflette sul fattore 1 / r 2 che compare nella legge coulombiana dell'interazione elettrostatica.
A ogni vertice di emissione o assorbimento di un fotone virtuale si associa un fattore che ne rappresenta il contributo all’ampiezza di probabilità, detto “costante di accoppiamento”. Questa caratterizza il tipo d’interazione e (per quelle elettromagnetiche) si riflette sul valore della "costante di Coulomb" k che appare nella legge d’interazione elettrostatica.
......
F
es
= k Qq / r
2
,
......|
Fig. 7. Conversione di fotoni (linee tratteggiate) con creazione di coppie
elettrone-positrone, in una interazione di neutrino vista in una camera a bolle.
Immagine
CERN Courier
|
Fig. 8. In alto: Conversione di fotone con creazione di una coppia elettrone-positrone.
In basso: una coppia elettrone-positrone si annichila in un fotone
Immagini tratte da
Cronodon
|
Creazione e annichilazione di coppie elettrone-positrone
Secondo la relazione einsteiniana E = mc 2 , l’energia si può convertire in materia e viceversa. L’energia di un fotone può essere così convertita in un elettrone e- accompagnato dalla sua antiparticella, un positrone e + . Per essere precisi, notiamo che questo processo avviene allorchè il fotone attraversa uno strato di materia e interagisce con i nuclei atomici in essa contenuti.
La figura 7 mostra due esempi di questo processo di “creazione di coppia” in un dettaglio di un famosa interazione di neutrino, registrata al CERN in una camera a bolle ” e discussa in Interazione Elettrodebole . I fotoni (elettricamente neutri) non sono visti e nello schema in basso sono indicati da linee tratteggiate. L’elettrone e il positrone si dipartono da essi a V e sono caratterizzati da tracce curvate in senso opposto da un campo magnetico, in virtù dell’opposto valore della loro carica elettrica.
La relazione einsteiniana massa-energia permette anche il processo inverso: la “annichilazione” di una coppia elettrone-positrone in un fotone. I due processi sono rappresentati “alla Feynman” in figura 8. Si noti che nei diagrammi di Feynman le antiparticelle (un positrone e + in figura) sono caratterizzate da una freccia in senso opposto rispetto a quella delle particelle: questa è una convenzione giustificata da considerazioni di fisica.
Una coppia virtuale nascosta nel mediatore
Continuiamo a ragionare per avanzare nella “costruzione” di una visione dell’interazione elettrone-elettrone tramite i diagrammi di Feynman secondo la QED. Come in L’enigma dell’interazione a distanza e i “quanti” , ci limiteremo a considerarli come strumento grafico e a livello qualitativo.
Conversione e annichilazione si possono susseguire anche per il fotone virtuale, secondo il diagramma di Feynman in figura 6 a destra. Con l’energia del fotone virtuale è creata una coppia (virtuale) elettrone-positrone, che è necessariamente riconvertita in un fotone all’interno del processo. In tal modo, la catena fotone-coppia-fotone resta virtuale e confinata all’interno del processo. Nel suo complesso, essa ha funzioni di mediatore.
Come detto precedentemente, nell’espressione dell'ampiezza di probabilità complessiva a ciascuno dei vertici di emissione e assorbimento del fotone virtuale (presenti in ambedue i diagrammi figura 6) va associato un fattore pari alla costante di accoppiamento. A esso corrisponde una probabilità notevolmente minore di 1. Il diagramma in figura 6 a destra presenta due vertici in più (quelli di creazione e annichilazione della coppia elettrone-positrone), a ciascuno dei quali va associato lo stesso fattore di cui sopra, Quindi tale diagramma risulta doppiamente sfavorito in termini di ampiezza di probabilità.
Ne consegue che il diagramma con coppia virtuale elettrone-positrone porta una piccola correzione (dell’ordine del %) alla probabilità che il processo avvenga unicamente in base al diagramma con il solo fotone.
Diagrammi di Feynman e approssimazioni successive
Secondo la precisione che si vuole raggiungere nella descrizione quantitativa di un processo (l’interazione elettrone-elettrone nel caso di cui sopra), si procede per approssimazioni successive considerando diagrammi progressivamente più complessi e con un maggior numero di vertici. Conseguentemente il loro contributo è via via decrescente. La figura mostra i primi due diagrammi che descrivono l'interazione elettrone-elettrone.
La rappresentazione del fenomeno è data dal complesso dei diagrammi di Feynman considerati. Matematicamente, le corrispondenti ampiezze di probabilità vanno addizionate secondo i dettami della fisica quantistica. Il loro valore progressivamente più basso assicura che esse costituiscano solamente piccole correzioni.
|
Fig. 9. Bollicine, in un manifesto di Jean d Ylen (1921)
Immagine
Pinterest
|
Non ci si stupisca se, traducendo i diagrammi in espressioni matematiche secondo le regole di Feynman, la legge fisica è rappresentata da una somma di espressioni invece che da una singola come per esempio nella legge d’interazione elettrostatica. Chi ha ordinato che una legge fisica debba essere rappresentata da una singola espressione matematica e non da una somma?
Con la suddetta metodologia, la QED ha raggiunto precisioni straordinarie nella descrizione dei fenomeni. Tramite confronto con dati sperimentali di paragonabile precisione, la sua validità è stata verificata con una accuratezza fino all’ordine di grandezza di parti per milione come detto in Interazioni elettromagnetiche “alla Feynman” .
Polarizzazione del Vuoto
La formazione di una coppia virtuale elettrone-positrone entro un fotone virtuale va sotto il nome di “polarizzazione del Vuoto”. La parola viene dal fatto che si creano contemporaneamente due specie di poli opposti (elettrone e positrone, e in generale particella-antiparticella), inseparabili come i poli Nord e Sud di una calamita.
Le coppie particella-antiparticella formatesi nel Vuoto sono come “bollicine” quantistiche-relativistiche, aventi vita temporanea. La QED trasforma la visione del Vuoto da spazio inerte a vivo.
Questo effetto evoca, infatti, l’immagine delle bollicine nello spumante versato nei nostri bicchieri da una bottiglia appena aperta (figura 9). All’apertura della bottiglia la pressione esterna cala improvvisamente e mette il gas disciolto nella massa del liquido in “fuori gioco” ossia, detto con parole scientifiche, in condizioni di sovra-saturazione rispetto alla Legge di Henry (1803). Al gas non resta che uscirne formando bollicine.
|
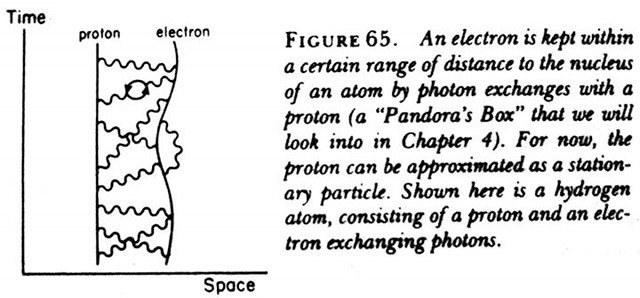
Fig. 10. Il legame atomico dell’Idrogeno raffigurato ispirandosi alla QED
Immagine
Feynman - Smolin
|
Il vuoto atomico si anima
La figura 10, tratta dal famoso libro divulgativo di Richard Feynman dal titolo QED: la strana teoria della luce e della materia (Princeton University Press - Adelphi, 1985), sintetizza – in un’immagine che non è un diagramma di Feynman - la visione che la QED ispira per l’interazione tra protone e elettrone nell’atomo di Idrogeno. Fotoni virtuali sono continuamente emessi e riassorbiti, e danno eventualmente luogo a “bollicine” particella-antiparticella. Il vuoto atomico è “virtualmente” animato.
Chi è Mr. Electron?
La QED porta anche a una nuova descrizione quantistica-relativistica di particella elementare, che ci mette di fronte a interrogativi fondamentali ma complessi. Ne daremo un accenno.
Secondo la QED, un processo è rappresentato dall’insieme dei diagrammi di Feynman che sono necessari per raggiungere la precisione voluta, via via più complessi e a livelli di probabilità più basso.
Fig. 11. A sinistra: un elettrone “nudo”. Al centro: un elettrone "vestito" da un fotone virtuale emesso e riassorbito
A destra: come al centro, con una coppia virtuale elettrone-positrone generata dal fotone virtuale - Immagini
Cronodon
Anche una particella come l’elettrone è rappresentata da un complesso di diagrammi di Feynman. La figura 11 ne mostra alcuni. A sinistra è mostrato il diagramma più elementare, corrispondente al cosiddetto “elettrone nudo”. Nel diagramma al centro un fotone virtuale è emesso e riassorbito. Quello a destra mostra che esso può generare una coppia virtuale particella-antiparticella (in figura elettrone-positrone). In sostanza, l’elettrone nudo viaggia con il “rivestimento” previsto da altri diagrammi. Non solo il Vuoto non è vuoto, ma il confine tra pieno e vuoto non è netto.
Notate che questo effetto non ha nulla a che vedere con l’indeterminazione nella posizione dell’elettrone conseguente al “ Principio di Indeterminazione ”, già implicita nelle equazioni di Schrödinger e di Dirac.
Se siete curiosi, vedete in Appendice 2 come rispondere alla domanda: quale è la carica dell'elettrone?
Fig. 12. Maja desnuda e Maja vestida (circa 1800). Museo del Prado, Madrid - Immagini
Wikipedia
Maja e fisica quantistica
La rappresentazione dell’elettrone con una serie di diagrammi ripropone un interrogativo sul significato fisico della presenza di più di un solo diagramma. Rispondiamo ricorrendo alla Maja di Francisco Goya (1746-1828) come termine di paragone in fisica classica. La figure 12 mostra i suoi famosi dipinti Maja desnuda e Maja vestida. A ogni determinato istante, Maja è “o nuda o vestita”.
A un oggetto quantistico come l’elettrone succede qualcosa di completamente diverso, che non ha corrispondenti alla scala macroscopica ma va ugualmente accettato come realtà fisica. La scala microscopica della fisica quantistica richiede infatti un nuovo modo di pensare i fenomeni, come discusso in Pensare in Quantistico . L’elettrone può essere trovato in uno stato ("nudo" o "vestito") rappresentato da “uno qualsiasi” dei diagrammi di Feynman in figura 11, o da altri più complessi non mostrati. Ad ogni diagramma è semplicemente associata un (ampiezza di) probabilità. L’elettrone è rappresentato dal complesso dei diagrammi.
QED e spostamento di Lamb
I fotoni virtuali riassorbiti dalla loro sorgente (come quello nel diagramma centrale in figura 11) e le coppie virtuali elettrone-positrone (come nel diagramma a destra in figura 6) costituiscono esempi di circuiti che si chiudono su se stessi e non escono nel mondo esterno. Tuttavia, essi riflettono sulle previsioni fornite dalla QED. In particolare, l'aggiunta di diagrammi di Feynman influisce sulla determinazione dei livelli energetici degli elettroni atomici e porta a delle piccole correzioni che spiegano lo spostamento di Lamb rispetto ai livelli attesi in base al solo diagramma più elementare.
Fotoni virtuali in circuito chiuso con l'aggiunta di una bollicina (come nel diagramma a destra in figura 11) portano a piccole correzioni di piccole correzioni e quindi i loro effetti sono solitamente trascurabili. Questo è detto nel caso che siate stati tanto attenti da porvi la domanda.
Il bosone di Higgs e l’energia del Vuoto
Simmetrie e Interazioni Fondamentali espone come le Interazioni Fondamentali sono oggi formulate imponendo il rispetto di simmetrie dette “di Gauge”. Il bosone di Higgs: una rivoluzione rispetto al comune pensare e Rottura Spontanea della Simmetria e bosone di Higgs mostrano come si è giunti a predire l’esistenza del bosone di Higgs, ingrediente fondamentale per riprodurre nella teoria il fatto che le particelle possono avere massa non nulla.
Il concetto di Vuoto vede una nuova rivoluzione: il cosiddetto Vuoto pullula di bosoni di Higgs. Il fatto singolarmente nuovo è che al loro stato energetico più basso (quello che in fisica classica è lo stato di quiete) non corrisponde un’energia nulla. Quindi i bosoni di Higgs danno al Vuoto energia propria. Siamo passati da un Vuoto letteralmente vuoto a un Vuoto animato, e infine a un Vuoto con energia propria!
Le masse delle particelle note derivano dall'interazione con bosoni di Higgs secondo un quadro teorico coerente, ma al momento non appare nessun collegamento speciale tra esse, nessuna struttura all'interno della quale sia possibile riempire di significato i loro diversi valori. Il Vuoto ha ancora cose da dire sulle masse delle particelle e sulla sua stessa natura!
Fig. 13. Jackson Pollock, Number 8, 182 cm x 86 cm (1949);
Neuberger Museum
, New York - Immagine
Wikiart
Dare e prendere
Jackson Pollock con il suo “action painting” interagiva con la sua opera, facendone “emergere la vita propria” in un continuo “dare e prendere”. La figura 13 mostra un dipinto di Pollock. Solo dal vero se ne riceve il pieno impatto espressivo. Vedetene anche un dettaglio . Il titolo stesso “Number 8” manifesta che esso non è ammaestrato a dire qualcosa, ma parla liberamente il suo linguaggio avendo “vita propria”.
La Scienza segue un simile processo creativo, procedendo attraverso un continuo interagire con la Natura: vede, interroga sperimentalmente, vede, riflette, interroga e così via. Così stanno emergendo le proprietà del Vuoto e la sua “vita propria”.
Che cosa ci porta questa conoscenza? In Il Mondo è pieno di Vuoto abbiamo visto che la natura del Vuoto fu indagata già nella Filosofia dell'antica Grecia in relazione alla teoria atomistica. Forse anche allora c'era chi si poneva la stessa domanda. La risposta è venuta dalla Storia: lo sviluppo della nostra civiltà non sarebbe stato lo stesso senza l'impulso dato dal pensiero scientifico e filosofico greco. Anche oggi bisogna guardare avanti e pensare che la vera risposta verrà dalla Storia: quella ancora da scrivere.
Riferimenti bibliografici
Richard P. Feynman, La legge fisica (Modern Library – Bollati Boringhieri, 1965)
Richard P. Feynman, QED: the strange theory of light and matter - QED: la strana teoria della luce e della materia , Editore Princeton University Press (1965) - Adelphi (1989)
Quantum Electrodinamics (QED) , Cronodon
Robert Matthews, Nothing like a vacuum : what could be a permanent, decidedly nonzero source of energy in the Universe, with cosmic consequences? The vacuum is far from empty , New Scientist, (1995)
APPENDICE 1: L’atomo secondo Dirac
La Teoria della Relatività Speciale fu formulata nel 1905 e stabilì l’ equivalenza massa-energia secondo E = mc 2 .
Nel 1928 Paul A. M. Dirac (1902-84) con la sua magica equazione fornì una descrizione quantistica-ondulatoria dell’elettrone valida anche in regime relativistico (contrariamente all'equazione di Schrödinger), inoltre, comprensiva del suo “ momento angolare di spin ”. L’equazione di Dirac vale per tutte le particelle elementari con “numero quantico di spin” s=½, dette “ fermioni ”.
Di più, l’equazione di Dirac predisse la “necessaria” esistenza di anti-particelle. Nel 1932, ne fu scoperta la prima: l’anti-elettrone, comunemente detto “positrone” e indicato con il simbolo e + lasciando e- per l’elettrone.
Nella descrizione degli orbitali atomici dell’atomo di Idrogeno secondo l’equazione di Dirac, il “numero quantico di momento angolare totale” j è dato da un’opportuna combinazione di quello orbitale l e di quello di spin. Nell’usuale denominazione degli stati quantici, il valore di l è indicato da una lettera maiuscola S, P, … per l = 0, 1, … e gli stati con l = 0 e l = 1 sono rispettivamente denotati da nS j e nP j .
L’applicazione dell’equazione di Dirac porta a delle piccole correzioni (dell’ordine di 1%) ai livelli energetici degli elettroni atomici, dette di “ struttura fine ”. Esse derivano da effetti relativistici e dalla presenza sia di un momento angolare orbitale che di spin. In assenza di campo magnetico, i livelli energetici dipendono da n con una correzione di struttura fine funzione di j e non di l. Ne consegue che i livelli energetici di stati con gli stessi valori di n e di j sono identici (nel linguaggio scientifico “degeneri”) anche se caratterizzati da diversi valori del momento angolare orbitale, cioè di l.
Facciamo l’esempio pertinente allo spostamento di Lamb. Si ha lo stesso j = ½ da uno stato S (l = 0) con j = 0 + ½ e da uno stato P (l=1) con j = 1 - ½ , ove il secondo dei due termini proviene dal momento angolare di spin e (per lo stato P) dipende dal suo orientamento rispetto a quello orbitale. Nel caso n = 2 questi stati S e P sono rispettivamente denotati come 2S ½ e 2P ½ . I corrispondenti livelli energetici sono rigorosamente identici.
APPENDICE 2: Quale è la carica dell'elettrone?
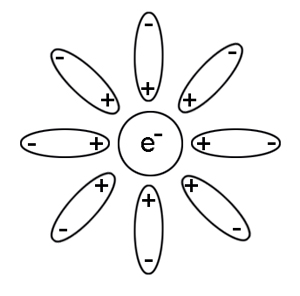
La figura 14 traspone il complesso di diagrammi che rappresentano l'elettrone (ai cui primi si riferisce la figura 9) in un’immagine che – al pari di quella in figura 10 – è ispirata alla QED senza avere il significato grafico-matematico dei diagrammi di Feynman. L’elettrone nudo è rivestito da coppie virtuali particella-antiparticella e “tutto accade come se" le (anti) particelle con carica elettrica positiva fossero attratte verso l’elettrone (con carica negativa) e tendessero a neutralizzarne parzialmente la carica elettrica negativa.
|
Fig. 14. Elettrone rivestito ispirandosi alla QED
Immagine
Plus Magazine – Frank Wilczek
|
Sorge un interrogativo fondamentale: a cosa corrisponde la “carica dell’elettrone” che troviamo sui libri di fisica classica? Non può essere che la carica vista a distanza macroscopica e quindi con quella dell’elettrone completamente “rivestito”.
Incalziamo con un’altra domanda. Come confermare sperimentalmente questa visione? Se essa è corretta, la carica dell’elettrone sperimentalmente misurata non ha un valore univoco: una particella di alta energia che penetri entro il “rivestimento” che neutralizza parzialmente l’elettrone nudo e gli si avvicini dovrebbe sperimentare un valore della carica dell’elettrone maggiore di quella della fisica classica. Questo effetto è stato riscontrato facendo collidere elettroni e positroni ad alta energia.
Immaginando di far collidere elettroni e positroni a energia sempre più alta, noterete con una certa apprensione che la carica apparente dell'elettrone aumenta sempre di più.
L'elettrone nudo è sperimentalmente inavvicinabile, altrimenti così continuando (teoricamente) troveremmo per esso una carica apparente addirittura infinita. Il serio problema che si pone è fortunatamente solo teorico, perché dal punto di vista sperimentale vi è un'ancora certa: il valore della carica dell'elettrone nella fisica classica, misurato a distanza macroscopica e solitamente indicato con il simbolo e.
Ma allora che fare della problematica carica infinita dell'inavvicinabile elettrone assolutamente nudo? La risposta teorica a questo interrogativo teorico è da "uovo di Colombo": ancoriamo anche la teoria al solo valore misurato e. La suddetta carica infinita perde drammaticità pratica e viene ridimensionata (in linguaggio tecnico "rinormalizzata") riassorbendola all'interno stesso della teoria. Questa è in sintesi la complessa procedura detta di “rinormalizzazione".
...
...
Professore Emerito di Fisica Sperimentale
Università di Napoli "Federico II"
Complesso Univ. Monte S. Angelo
Via Cintia - 80126 Napoli - Italy
Ultima Modifica 8 Anni 11 Mesi fa da Paolo.
Si prega Accesso a partecipare alla conversazione.
Tempo creazione pagina: 0.588 secondi