................ ................ ................

............................................................................... Fig. 1. Un cristallo di neve visto al microscopio elettronico entro un fiocco di neve - Immagine Wikipedia

...

......................... Nella vita esistono esigenze basilari, essenziali come amare, mangiare, bere, dormire, abitare. Vi sono esigenze personali, senza le quali non saremmo noi stessi: sapere, vivere la natura, … a ognuno mettere le sue. Ma vi sono quelle piccole cose a rigore inessenziali che assumono importanza perché colorano la vita: quale “togliersi uno sfizio”, come i napoletani essendone maestri dicono in pochissime parole essenzialmente intraducibili nella loro pienezza. In italiano sfizio può essere banalizzato in "gusto, diletto" (vedete Napoli Glossario ). Ma resta da vedere come fare per esprimere con altre parole il "togliersi", che ha un'implicazione psicologica molto più sottile degli usuali e invadenti "prendersi" o "cavarsi": come di cosa che va fatta per star meglio. Un esempio storico: " a sigaretta co ’o sfizzio ". Con l'emergere del contrabbando di sigarette già a fine '800 date le condizioni della città, il commercio era esercitato dalle donne, che nascondevano le sigarette sotto i vestiti e in particolare tra i seni: acquisto con sfizio. Offriamoci qui lo “sfizio scientifico” di capire come nel “Modello a quarks” degli “adroni" (tra cui "barioni" e "mesoni", vedete Protone, pione & adroni ) si costruisce un “cristallo a quarks”.

E' questa la denominazione che - evocando la simmetria della struttura cristallina determinata dagli atomi che la costituiscono - prendiamo la libertà di dare alle strutture simmetriche nelle quali il Modello a quarks situa i "numeri quantici" degli adroni.

Daremo per noto il contenuto di Simmetrie: protoni, neutroni e ... quarks , ove è seguito il percorso storico narrando come dalle simmetrie sperimentalmente osservate per gli adroni sono stata dedotte l'esistenza e le proprietà dei quarks. Qui effettuiamo il passo successivo, idealmente muovendoci in senso opposto: in base alle proprietà dei quarks svilupperemo il Modello a quarks degli adroni e ricostruiremo sistematicamente le simmetrie degli adroni per via teorica.


Anche un bel gioco scientifico

E' però uno sfizio impegnativo, da arditi semi-professionisti. Perché allora? Diamo prima le risposte "serie".

Anzitutto, è un buon esercizio pratico per illustrare il concetto di "stato quantistico" e capire "come funziona" la Meccanica Quantistica, con leggi che governano la nostra esistenza (siamo fatti di atomi, non è vero?) e le tecnologie di oggi, ma che sfuggono alla nostra esperienza sensoriale diretta perché avvengono a una scala dimensionale troppo piccola. Ritorneremo su questo nel capitolo conclusivo.

In secondo luogo, comprendere la struttura della materia è una ricerca di bellezza, a ogni scala dimensionale. Pensate ai cristalli di neve. Un potentissimo microscopio elettronico ne evidenzia la struttura e amplifica la bellezza, come vedete in figura 1. Capire la loro struttura e la loro formazione è tutt'altro che ovvio e richiede impegno, ma è affascinante. Se siete attratti dai cristalli di neve, visitate il Sito Web SnowCrystals .

............................................................................... ... Fig. 2. Simmetria per giocare e imparare Immagine Pianeta bambini

...

......................... I cristalli a quarks hanno la bellezza di una legge fisica prodotta dall'intelletto umano nella rappresentazione concettuale di un aspetto della Natura stessa. Possono ben suscitare altrettanto fascino dei cristalli minerali e meritare impegno. Vedremo come il Modello a quarks “costruisce” gli adroni con quarks come costituenti elementari. Secondo le loro specifiche proprietà, esso li situa ai vertici o in altri punti particolari di poliedri, i cristalli a quarks, che vanno visti in uno spazio astratto i cui assi cartesiani sono definiti da numeri quantici e non da coordinate spaziali x-y-z.

Ma è anche un gioco, e questo non è cosa da poco. Vi sono i "giochi di simmetria" per bambini (figura 2), e sono considerati molto educativi oltre che essere divertenti. Perché non lasciarsi tentare da un gioco di simmetria scientifico?

......

......................................................................... Fig. 3. Famiglie di leptoni e di quarks Immagine Scienza per tutti - Masella

......

..... La proprietà dei quarks che viene usualmente presentata è il cosiddetto "sapore", che li indica come quark down, up, strano, charm, bottom o top. La figura 3 mostra la suddivisione dei quarks in tre "famiglie" in base al sapore, simmetrica rispetto a quella dei " leptoni " (vedete Simmetrie e Interazioni Fondamentali ). Come i leptoni, i quarks hanno un "momento angolare di spin" - o "spin" - con valore s = ½ (vedete Lo spin e Spin e elicità dell-elementare ). Lo spin può essere in su o in giù. Una ulteriore proprietà dei quarks è il cosiddetto "colore", che può essere rosso, verde e blu. Come esposto in Viaggio nei colori: quarks e gluoni e riassunto in seguito, queste denominazioni provengono da una analogia con la "Teoria tricromatica del colore" e non hanno nulla a che vedere con l'usuale colore da noi percepito. Il colore è una proprietà specifica dei quarks, collegata alla loro Interazione Forte (vedete Interazione Forte ). Le proprietà dei quarks sono quantitativamente espresse attraverso "numeri quantici", che indicano anche i possibili stati assunti.

Isospin e simmetrizzazione dei numeri quantici di sapore

A parte il diverso valore della carica elettrica, neutrone e protone sono particelle molto simili. Il "numero quantico di isospin" è introdotto in Simmetrie: protoni, neutroni ... e quarks per "simmetrizzarli" differenziandoli solo attraverso un diverso valore dell'isospin e più precisamente della sua proiezione lungo un determinato asse: I₃ = -½..e rispettivamente +½ . L'asimmetria della loro carica elettrica (0 e +1) è irrilevante anche per il Modello a quark degli adroni, ed è stata tolta dal gioco dal simbolico "cartellino rosso".

La simmetria di isospin tra neutrone (costituito di quarks ddu, come sarà mostrato in figura 7) e protone (uud) è un riflesso di quella tra i quark down (in breve d) e up (u), anch'essi aventi isospin I₃ = -½..e rispettivamente +½ . Gli isospin I₃ dei quarks si sommano, infatti, a formare quelli degli adroni.

In altre parole, introducendo il concetto di isospin non si parla di neutrone o protone, né di quark down o up, ma di due valori simmetrici (-½ e +½ ) che possono essere assunti da un singolo "numero quantico di sapore" I₃ .

Aggiungendo altri sapori a down e up, si introducono addizionali numeri quantici di sapore analogamente simmetrizzati. In generale, i numeri quantici di sapore ammontano al numero di sapori di quarks considerati, meno 1.


Numeri quantici dei quarks

In sintesi, i quarks sono definiti attraverso "numeri quantici" riferiti a:

• ..“sapore”: rappresentato da un insieme di numeri quantici che li indicano come quark down, up, strano, charm, bottom o top, al pari di I₃ definiti in modo da rispettare simmetrie;

• ..“spin” s = ½, con per numero quantico m_s l'orientamento in su (↑ per m_s = ½) o in giù (↓ per m_s = - ½);

• ..“colore”: con per numero quantico l'essere rosso, verde o blu (vedete Viaggio nei colori: quarks e gluoni ).


Cartellini rossi

Notiamo l’esclusione di due proprietà che i quarks "si tirano dietro", ma non hanno un ruolo nel determinare la struttura degli adroni in base al Modello a quarks.

....................................................................................................... ..... Fig. 4. I primi cartellini rossi Danny Shanahan , The New Yorker (2014) - Immagine Patheos

.....

..................................................................... “Cartellino rosso” alle carica elettriche dei quarks: la “Interazione Elettro-Magnetica" non ha alcun ruolo nel determinare i numeri quantici degli stati quantistici degli adroni, governati dalla “Interazione Forte” la quale è anche responsabile della coesione del nucleo atomico (vedete Interazione Forte ). Le cariche elettriche saranno riammesse in campo a partita finita nel tirare somme e necessariamente ritrovare la carica elettrica degli adroni. Ma non preoccupatevi: le cariche frazionarie (-⅓ o +⅔) assegnate ai quarks assicurano che si ritrovino le corrette cariche degli adroni. “Cartellino rosso” alle masse dei quarks, estranee alle simmetrie e neppure ben definibili: conosciamo le masse degli adroni ma (secondo E = mc2 ) esse dipendono anche dalle energie di legame dei quarks negli adroni stessi. Le masse in generale devono stare fuori campo.

......
Come anticipato, utilizziamo ora il Modello a quarks per ricostruire teoricamente gli adroni e le loro proprietà. Procederemo in due passi. Per prima cosa, rappresenteremo gli adroni mediante "stati quantistici" individuati in base a simmetrie. In secondo luogo collegheremo questi stati quantistici agli adroni come "particelle fisiche" osservate sperimentalmente.


Stati quantistici e simmetria: cardine metodologico

La Meccanica Quantistica ha leggi incredibili per il senso comune ma di validità provata e riprovata. Tra queste vi è la possibilità di rappresentare rappresentare lo stato di una particella o di un sistema prendendo come riferimento un insieme di "stati quantistici" (vedete Onde e particelle per pedoni molto curiosi ), definito secondo un criterio a scelta. La scelta è effettuata in base a razionalità e logica, secondo la fisica che si vuole mettere in luce nel modo più semplice.

L'espressione "cardine metodologico" nel titolo del capitolo si riferisce all'uso di questa libertà per scegliere un sistema di stati quantistici che rispetti criteri di simmetria. Vediamone il principio concettuale riferendoci allo spin per un sistema di due quarks.


Facce di due monete

Iniziamo dalla vita quotidiana e immaginiamo di formare tutte le possibili combinazioni degli orientamenti di due monete, ciascuna delle quali può mostrare “testa” (↑) o "croce" (↓). Le combinazioni possibili sono quattro: ↑↑, ↑↓, ↓↑ e ↓↓. Si noti che non tutte le combinazioni rispettano la simmetria per scambio di una moneta con l'altra: le combinazioni laterali restano uguali a se stesse, ma non quelle centrali.

................................................................................................ Fig. 5. Le Tre Grazie (II sec. d.C.) Gruppo scultoreo in marmo di Epoca Imperiale Romana rinvenuto presso Villa Cornovaglia sul Colle Celio a Roma Museo del Louvre, Parigi - Immagine Archeo

........

..................................................................... Spin di due quarks Lo spin è rappresentato da un vettore, come lo è il momento angolare di un corpo rigido in rotazione. I quarks hanno spin s = ½. Ciascun quark può avere il suo spin orientato in su (↑) o in giù (↓). Consideriamo ora il sistema di due quarks riferendoci esclusivamente al loro numero quantico di spin, tanto che in breve lo chiameremo sistema di due spin. Il modo banale di rappresentare lo stato del sistema di due spin consiste nel riferirsi alle possibili "combinazioni" degli spin. Come per le monete, le combinazioni possibili sono ↑↑, ↑↓, ↓↑ e ↓↓. Le leggi quantistiche permettono di fare di più. Sfruttiamo la libertà di rappresentare l'insieme dei due spin mediante "stati quantistici", costituendoli di “miscugli” delle combinazioni che abbiamo formato. La scelta dei miscugli è a priori libera anche nel segno (+ oppure -) con cui le singole combinazioni entrano nel miscuglio. Formiamo quindi "stati quantistici" in ugual numero a quello delle combinazioni, ma con simmetria definita rispetto allo scambio del primo con il secondo spin. Essi sono i seguenti: ..........“tripletto simmetrico”.................↑↑, (↑↓ + ↓↑), ↓↓ ..........“singoletto anti-simmetrico”............(↑↓ - ↓↑).

Come si vede, nel tripletto simmetrico nulla cambia scambiando i due spin. Invece, lo stato anti-simmetrico cambia segno, da cui il nome. Per semplicità è omesso un fattore di normalizzazione degli stati quantistici misti (tra parentesi), che presi come scritti paiono corrispondere a più di due spin.

La figura 5 mostra quanta eleganza può avere un tripletto: ci serva per fissare nella mente il concetto di stato quantistico simmetrico e la sua utilità.


Lasciamoci guidare dalle Simmetrie

Abbiamo visto come definire gli stati quantistici di un sistema costituito dagli spin di due quarks seguendo il criterio indicato da una simmetria. La metodologia porta lontano. Anzitutto, la matematica sviluppata è applicabile anche agli altri numeri quantici dei quarks, e non solo allo spin.

Inoltre, la metodologia può essere estesa da due ai tre quarks che costituiscono i "barioni" (la famiglia del protone e del neutrone), con ciascun quark in uno stato definito da propri numeri quantici. Con le dovute differenze, il discorso vale anche per i "mesoni" (la famiglia del pione), costituiti di un quark e di un antiquark. Per una classificazione degli adroni in generale, vedete Protone, pione & adroni ).

Essendoci esercitati con lo spin, siamo equipaggiati per capire a grandi linee come "costruire" gli stati quantistici corrispondenti ai barioni nel Modello a quarks lasciandoci condurre dalle simmetrie come Dante da Virgilio nella Divina Commedia:

E’ come riprodurre un cristallo di Salgemma, con la sua simmetria, in base alle caratteristiche degli atomi che lo costituiscono: Na e Cl.


Da quarks a cristalli a quarks

Focalizziamo l'attenzione sui barioni - costituiti di 3 quarks - con spin totale J = ½ e vediamo come costruire cristalli a quarks, formati in base a "stati quantistici" retti da simmetrie. In un successivo discorso di sintesi includeremo il passo finale e vedremo come partendo da quarks giungiamo barioni come "particelle fisiche".

Siamo al "gioco scientifico" promesso inizialmente, che consiste nel costruire i cristalli a quarks. Nel gioco del Lego , prendiamo mattoncini sciolti dalle loro scatole e li assembliamo direttamente per costruire strutture. Il nostro gioco porta da quarks come “oggetti sciolti” a multipletti di stati quantistici costruiti con quarks come “costituenti elementari” e a cristalli a quarks.

Se ne è visto il cardine metodologico per lo spin del sistema di due quarks. Per costruire i multipletti che costituiscono un cristallo a quarks, il gioco è concettualmente identico ma praticamente più complesso e impegnativo. Dobbiamo prendere tre quarks, e per ciascuno considerare non solo lo spin, ma anche sapore e colore. E combinare il tutto opportunamente, secondo regole e dettati quantistici.

Per cucinare uova al tegamino, non avete bisogno di ricetta. E' necessaria per piatti raffinati e complessi come i cristalli a quarks: la avete nell’Appendice Ricetta per barioni "alle simmetrie". Se preferite continuate qui e godetevi il piatto pronto e fumante con solo qualche indicazione su come è stato cucinato, senza offrirvi il piacere di cucinarlo voi stessi. Potete anche leggerla per sommi capi, fino a comprendere come funzionano le cose.

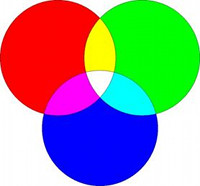
................................................... Fig. 6. Miscugli dei colori fondamentali rosso, verde e blu Immagine M.A. Dodero

.....

...................... Iniziamo con il colore. Le osservazioni sperimentali all’origine dell'ipotesi del colore dei quarks indicano che tutti gli adroni hanno colore neutro. D'altra parte, con la figura 6 la summenzionata teoria tricromatica del colore" mostra che sovrapponendo i 3 colori rosso, verde e blu in pari proporzioni si ottiene un colore neutro. Di conseguenza, i 3 quarks costituenti i barioni devono avere colori tutti diversi. Si formano poi separatamente per spin e sapore formando le banali combinazioni e si individuano i rispettivi multipletti, mantenendo per lo spin quelli che corrispondono alla spin totale voluto J = ½ . Infine, si formano le combinazioni dei multipletti di spin e sapore, mantenendo quelli che rispondono alle condizioni dettate dal fatto che i quark hanno spin s = ½ e sono quindi "fermioni" (vedete Lo spin: bosone o fermione? ). E il gioco è fatto: abbiamo i cristalli a quarks per i barioni con spin totale J = ½ , come volevamo.

Come si è detto, i cristalli a quarks sono costruiti in base a simmetrie in uno spazio astratto con per assi cartesiani i numeri quantici di sapore che li caratterizzano. Ciascun stato quantistico viene situato in un punto del suddetto spazio astratto, con ciascuna sua coordinata data da un numero quantico che è la somma dei corrispondenti numeri quantici dei suoi 3 quarks. Non è l'usuale spazio fisico tridimensionale nel quale si sviluppano i cristalli minerali.

Gli stati quantistici costituiti di quarks con sapori scelti tra i soli 2 down e up sono differenziati e definiti da solo 1 numero quantico di sapore, l'isospin I₃ . Come detto sopra, per 2 sapori si ha 2 - 1 = 1 numero quantico di sapore. Per essi basta 1 dimensione, e infatti in figura 7 gli stati quantistici del neutrone e del protone sono situati sull'asse di isospin.

Consideriamo ora 3 sapori dei quarks, includendo anche il quark strano: si passa alle 3 - 1 = 2 dimensioni di un piano, come mostrato in figura 7. Gli stati quantistici sono disposti simmetricamente secondo un "ottetto", con sei di questi stati ai vertici di un esagono e due sovrapposti al suo centro.

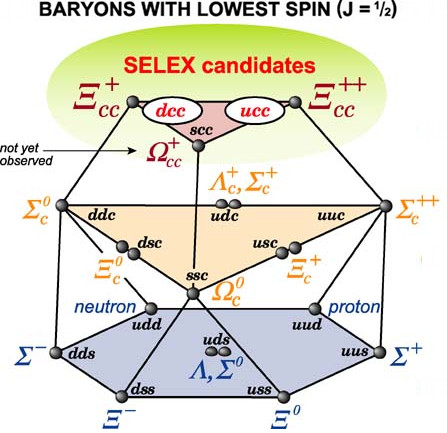
Gli stati quantistici costituiti di quarks con sapori scelti tra i 4 down, up, strano e charm sono caratterizzati da 4 - 1 = 3 numeri quantici di sapore: il cristallo a quarks è un poliedro tridimensionale ed è mostrato in figura 8. L'ottetto in figura 7 ne costituisce la base.

Se volessimo considerare più di 4 sapori, il cristallo a quarks si svilupperebbe in un "iper-spazio", con più di 3 dimensioni e praticamente impossibile da rappresentare graficamente: non vogliamo.

Fig. 7. Protone e neutrone (in alto) nell'ottetto dei barioni con spin totale J = ½ e costituiti di quarks u, d, s Immagine The mathematical poet - Tumbir

...

Fig. 8. Il cristallo a quarks dei barioni con spin totale J = ½ costituiti di quarks u, d, s, c. La figura a fianco ne è la base Immagine SELEX experiment - Fermilab

Da quarks a barioni: una sintesi con l'arte astratta

Con l'arte astratta abbiamo il puro piacere della contemplazione della bellezza, e possiamo talvolta godere della libertà di vedervi rappresentato quello che è nella nostra mente e fissarne i concetti. Il bel dipinto della "signora della pittura astratta" Carla Accardi (1924-2014) in figura 9 offre ambedue le possibilità.


I quarks appartengono al mondo della “realtà fisica”: vediamoli nel campo di colore paglierino alla sinistra del dipinto. Il gioco scientifico che porta dai quarks ai cristalli a quarks - intellettualmente molto più bello e intrigante del gioco del Lego - conduce dai quarks nel cielo astratto e meno conosciuto degli stati quantistici, individuati in base a simmetrie: vediamolo nel campo azzurro al centro del dipinto.

Dopo il volo sul piano astratto, dobbiamo atterrare e passare di nuovo nel mondo fisico: gli adroni che vediamo sperimentalmente sono "particelle fisiche". A destra del dipinto, vedete di nuovo il colore paglierino del mondo fisico. Il tutto è connesso dal pensare e ragionare: indovinate il colore corrispondente.

La corrispondenza tra stati quantistici e particelle fisiche è diretta per i vertici dei multipletti (o poliedri), caratterizzati dalla presenza di un unico stato quantistico. Ma talvolta vi è sovrapposizione di stati quantistici, come per i due stati centrali nell’ottetto di figura 7. In tali casi, le particelle fisiche corrispondono a “miscugli” degli stati quantistici, secondo le regole quantistiche.

Le proporzioni del miscuglio non hanno nulla a che vedere con le simmetrie. Esse sono determinate dalle interazioni tra quarks che generano il loro legame nei barioni, ma le energie di legame hanno avuto il cartellino rosso insieme alle masse. Possiamo dedurre le proporzioni del miscuglio solo dall'analisi di dati sperimentali. In Interazione Forte leggete di una teoria - la "Quanto-Cromo-Dinamica" (QCD) - che in linea di principio potrebbe farlo, ma la complessità del calcolo lo rende difficilmente accessibile.


Gli stati quantistici: oltre la banale realtà

A un livello più generale del Modello a quarks, il discorso fatto è importante per capire la peculiare proprietà che ha Meccanica Quantistica di farci vivere e operare in un mondo diverso, astratto ma strettamente connesso con la realtà: quello degli "stati quantistici" propri dei fenomeni che studiamo, nel caso qui trattato definiti in base a considerazioni di simmetria. Come esempio, il capitolo Spin di due quarks inizia nel mondo degli spin come lo vedremmo banalmente e ci porta in un altro, "trasfigurato" in base a criteri di simmetria.

Abbiamo detto "trasfigurato" nel (povero) tentativo di trovare una parola del linguaggio quotidiano che possa descrivere l'indescrivibile, se non nel rigoroso linguaggio quantistico. Alla voce " trasfigurazione ", il Grande Dizionario Italiano Gabrielli la definisce "mutamento di figura, di aspetto, di apparenza" e porta come esempio "la trasfigurazione della realtà nella fantasia". Sono fantasia - e bella - le trasfigurazioni che ci divertono in Harry Potter ( video e figura 10).

La Meccanica Quantistica non è fantasia. L'esistenza di una realtà quantistica astratta che sovrasta e governa quella banale è concettualmente sconvolgente. Anche e soprattutto per chi non conosce la Meccanica Quantistica e non ha neanche avuto il modo di farvi la cosiddetta "abitudine", che alle persone non attente possono offrire la ottusa comodità di fare anche senza riflettere.

Non è solo questo. Gli stati quantistici sono alla base di tante tecnologie ormai parte della vita di oggi e potranno entrare ancor di più nella vita di un domani. Leggete ad esempio Da Alan Turing al calcolo quantistico .

................................................................................................ Fig. 11. Capita anche questo! Francesco Tullio Altan - Immagine Comunità Cristiana

......

..... Riflettere, semplicemente riflettere In assenza di una formazione di base in Meccanica Quantistica, l'argomento trattato non sarà risultato semplice. Gli avventurosi avranno voluto fare come San Tommaso (apostolo-scienziato?), del quale si dice "San Tommaso non ci crede finché non ci ficca il naso". Ne valeva comunque la pena, come vale la pena vedere rappresentato nel famoso dipinto del Caravaggio - riportato in Neutrini e implosione gravitazionale - l'episodio evangelico da cui è tratto il detto popolare sopra citato. Ma se avete seguito i concetti esposti, avrete forse capito di più di certi cosiddetti specialisti che non prendono ii tempo per pensare e riflettere. Come fanno anche altri personaggi (figura 11).

................................................................. Fig. 12. Pellegrino Artusi La scienza in cucina e l'arte di mangiar bene Edizione originale (1891) - Immagine Wikiwand

......

..... Che la Cucina sia un’Arte e che abbia a che fare con la Scienza lo aveva capito Pellegrino Artusi - potremmo anche dirlo l'Alessandro Manzoni della cucina italiana - e detto anche nel titolo del suo storico e diffusissimo libro La scienza in cucina e l'arte di mangiar bene , del quale la figura 12 mostra il frontespizio nell’edizione originale del 1891. Vediamo ora che cosa può avere a che fare la Scienza con la Cucina. Per descrivere la struttura degli adroni in termini di quarks come costituenti elementari, è necessario comprendere come trasferire la nostra visione dal “mondo fisico” di particelle visibili sperimentalmente - adroni e i quarks - al mondo astratto di "stati quantistici" definiti in base a simmetrie. L' argomento non è difficile, ma complesso. Può divertire - o almeno essere sdrammatizzante - trattarlo come una ricetta di cucina. In questo modo può forse anche diventare "digeribile", pur se la parola barioni proviene dal greco βαρύς (pesante). Diamo la ricetta per il “Modello a quarks” dei barioni con spin totale J = ½ . I barioni sono costituiti di tre quarks, con spin s = ½. Tuttavia, il metodo è applicabile ad altri barioni e ai mesoni. INGREDIENTI Quarks dei sapori che desiderate, ciascuno preso con i propri numeri quantici di sapore, spin e colore.

............................................ .....

.....

..................................................................... Colore •..Come per tutti gli adroni, gli stati quantistici devono avere colore globalmente neutro. In particolare, i 3 quarks dei barioni devono avere colore diverso (figura 6, riportata a fianco come icona). •..Matematicamente, la neutralità del colore implica una simmetria rispetto a scambi di colore (invece, per esempio, un oggetto rosso cambia colore se si scambia il rosso con il blu). Una simmetria rispetto a scambi di colore ne implica anche una rispetto allo scambio dei quarks che li portano. •..Tenere presente.

Carattere dei quarks
•..I quarks hanno spin s = ½ e sono quindi "fermioni" (vedete Lo spin: bosone o fermione? ): vogliono essere i soli con i propri numeri quantici, in base al Principio di Esclusione di Pauli . Matematicamente, gli stati quantistici devono essere anti-simmetrici (cambiare segno) per scambio di due quarks.
•..Tenere presente.

............................................

.....

..................................................................... Spin •..Prendere esclusivamente gli spin. •..Iniziare con il mescolare gli spin di due quarks e formare il tripletto simmetrico ↑↑, (↑↓ + ↓↑), ↓↓ corrispondente alla figura 3 riportata a fianco come icona, e il singoletto antisimmetrico (↑↓ - ↓↑). •..Aggiungere lo spin del terzo quark e un pizzico di curiosità. Mescolare. •..Formare i multipletti per gli spin dei tre quarks, con ciascun multipletto definito in base a un suo specifico criterio di simmetria. •..Selezionare i multipletti con spin totale J = ½ . •..Mettere da parte.

Sapore
•..Considerare solo il sapore e i numeri quantici corrispondenti ai sapori scelti per gli ingredienti.
•..Come per lo spin, iniziare con il mescolare i numeri quantici di sapore di due quarks e formare i relativi multipletti caratterizzati da simmetria.
•..Aggiungere il numero quantico di sapore del terzo quark e un pizzico di curiosità. Mescolare.
•..Formare i multipletti per i numeri quantici di sapore dei tre quarks, con ciascun multipletto definito in base a un suo specifico criterio di simmetria.
•..Mettere da parte.

...........................................................

.....

..................................................................... Spin e sapore •..Prendere tutti i multipletti di spin e sapore, precedentemente formati e messi da parte. Aggiungere una dose di curiosità secondo gusti e inclinazioni. •..Formare tutte le loro combinazioni. •..Metterle da parte, annotando il tipo di simmetria che le caratterizza per scambi di due quarks. Spin, sapore, colore e carattere dei quarks Il carattere dei quarks richiede l’anti-simmetria degli stati quantistici. La loro componente di colore è simmetrica. Per assicurare un’anti-simmetria globale, selezionare le combinazioni anti-simmetriche di spin e sapore e gettare le altre.

•..Disporre in un bel piatto da portata, come indicato in figura 7 o in figura 8 (riportata a fianco come icona), secondo che il numero di sapori di quarks considerato sia 3 o 4.
•..Portare a tavola e, se soddisfatti, brindare con un buon vino profumato.



Nota: L'argomento è trattato in testi specialistici di particelle elementari, come per esempio: F. Halzen e A.D. Martin, Quarks and leptons , J. Wiley & Sons (1984). E' disponibile anche in pdf , ma richiede una adeguata preparazione.



.