Simmetrie e Principi di conservazione
- P. Strolin
-
Autore della discussione
- Offline
- Premium Utente
-
Less
Di più
12 Anni 7 Mesi fa - 9 Anni 2 Settimane fa #83
da P. Strolin
Per illustrare la portata dell'argomento trattato in questo articolo nello sviluppo della cultura umana, iniziamo con le parole scritte da Hermann Weyl nella prefazione del suo libro Symmetry (1952) per chiarirne gli intenti:
Esprimiamo in altre parole e portiamo ai nostri tempi lo spirito di Hermann Weyl. La simmetria si manifesta anche visivamente in Natura e da tempi antichissimi è presente nella cultura umana: vedete, per esempio, il misterioso cerchio megalitico di Stonehenge rappresentato in figura 1 da una preziosa testimonianza. La Fisica ha portato a capire che la simmetria è anche radice profonda della struttura del mondo che ci circonda al livello più fondamentale - quello delle particelle elementari - e delle forze che la determinano: lo mostra la figura 2. Tutto poggia su simmetrie.
Questo mostra che, al suo livello più alto, Fisica è Cultura nel senso più largo del termine. In una sintesi complessiva, lo sforzo di assorbire intellettualmente concetti e aspetti tecnici di questo articolo e di Simmetrie e Interazioni Fondamentali vi premierà con la soddisfazione di rendervene concretamente conto.
Il tracciato dell'articolo
La figura 3 dipinge in forma scherzosa un evento della vita di tutti i giorni, che accade al momento del talvolta doloroso risveglio e che, con un poco di fantasia, possiamo interpretare come un effetto della legge di conservazione della quantità di moto , nel caso particolare di corpo in quiete.
In quest'articolo illustriamo un fondamentale sviluppo del pensiero scientifico avvenuto all'inizio del Novecento, con l'avvento della cosiddetta fisica moderna: il " Teorema di Noether ", secondo il quale a ogni legge di conservazione corrisponde una simmetria e viceversa.
Con il Teorema di Noether, a livello profondo le "leggi di conservazione" classicamente regnanti assolute con la denominazione "principi" si trovano deducibili da una simmetria, e "conservazioni" considerate empiriche salgono in nobiltà al livello di "leggi" grazie a una simmetria che le sostiene. E questo non solo nell'ambito della fisica classica, ma anche nel mondo quantistico fino al livello fondamentale delle particelle elementari.
Inizieremo a vedere che - partendo dal Teorema di Noether - le simmetrie permettono di andare anche oltre verso aspetti dinamici e giungono a manifestarsi come fondamento di una nuova visione delle Interazioni Fondamentali, esposta in Simmetrie e Interazioni Fondamentali . Ne sono strumento le simmetrie rispetto alle cosiddette "Trasformazioni di Gauge" e in particolare quelle dette "Locali". Le introdurremo.
Leggi di conservazione
Cosa hanno in comune le figure 4 e 5, pur su scale dimensionali incomparabili? Andiamo in bicicletta senza pensare che non cadiamo grazie alla " legge di conservazione del momento angolare " nel moto di rotazione delle ruote (figura 4), che agiscono come un giroscopio . Guardiamo il cielo e non pensiamo che la stessa legge regola il moto dei corpi celesti, per esempio la rotazione delle stelle in una galassia (figura 5).
Leggi di conservazione come quella del momento angolare hanno carattere generale e fondamentale. Secoli di pensiero scientifico hanno portato alla loro concezione da parte di giganti scientifici quali Cartesio, Newton e Huygens.
Simmetrie
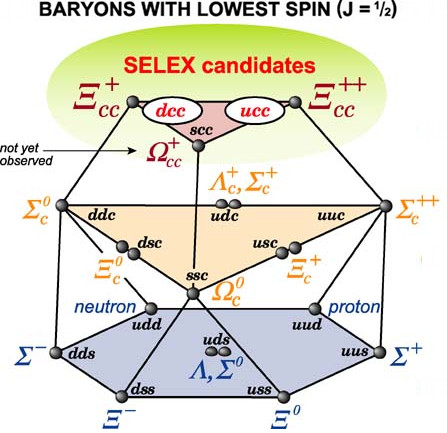
Due immagini sintetizzano simbolicamente la fondamentale importanza delle simmetrie nella struttura del mondo organico e inorganico. In figura 6 vedete l' Uomo Vitruviano " nel famoso disegno di Leonardo da Vinci (1452-1519), databile al 1490 circa e conservato alle Gallerie dell'Accademia a Venezia. La figura 7 mostra la struttura dei barioni con spin J = ½ costituiti di quarks down, up, strano e charm nel Modello a quarks e offre un esempio dell'importanza delle Simmetrie nella fisica moderna (vedete e Simmetrie: protoni, neutroni e ... quarks ).
Teorema di Noether
Tra il 1915 e il 1918 Emmy Noether pose una fondamentale pietra miliare della Scienza dimostrando che - in linea generale - le leggi di conservazione sono legate a simmetrie ossia a invarianze rispetto a trasformazioni, per quanto detto in Simmetrie: dai solidi platonici alla struttura cristallina . Più precisamente esso afferma che a ogni simmetria delle leggi fisiche per una trasformazione di tipo continuo corrisponde una grandezza fisica conservata, cioè un legge di conservazione. E viceversa a ogni grandezza fisica conservata corrisponde una simmetria.
Il "Teorema di Noether" fu praticamente ignorato per mezzo secolo. Lo fu la stessa Emmy Noether, salvo che in ristretti ambienti scientifici. Ma la portata pratica del suo teorema è vasta e profonda.
Anzitutto, stabilendo in modo formale una diretta connessione tra leggi di conservazione e simmetrie - ambedue fondamentali - diventa il loro "anello di congiunzione". Le leggi di conservazione non appaiono più necessariamente come "principi" nel senso letterale della parola e escono dall'originario isolamento assiomatico. Questo aspetto è discusso nel presente articolo. Simmetrie e Interazioni Fondamentali ne estende il discorso e giunge a individuare nelle simmetrie il fondamento teorico delle Interazioni Fondamentali. Oggi le simmetrie appaiono quindi essere la base del livello più profondo della conoscenza. Guardate di nuovo la bella immagine di Stonehenge in figura 1 - il nostro punto di partenza - per rendervi conto del progresso fatto dalla cultura umana.
Leggi di conservazione dell'energia, della quantità di moto e del momento angolare
Vediamo il messaggio dato dal Teorema di Noether in relazione alle trasformazioni spaziali e temporali: la legge di conservazione dell'energia deriva da una simmetria delle leggi fisiche rispetto a una traslazione temporale, quella della quantità di moto da una rispetto a una traslazione spaziale e quello del momento angolare da una rispetto a una rotazione spaziale.
In altre parole, l'energia non fosse conservata le leggi fisiche non sarebbero invarianti nel tempo. Analogamente per quantità di moto e traslazione spaziale, al pari di momento angolare e rotazione spaziale. In pratica, le simmetrie assicurano che le leggi fisiche abbiano validità universale e perenne. Oltretutto, se così non fosse sarebbe un gran disastro. E' una riprova della natura assolutamente fondamentale delle simmetrie.
Con un grande balzo in avanti, il Teorema di Noether si ricollega alle origini della Scienza moderna e cioè alla questione generale dell'Invarianza delle leggi fisiche, che è alla base della Relatività Galileiana e della Teoria della Relatività Speciale di Einstein come discusso in Simmetrie e Relatività Speciale e diviene postulato fondamentale nella Teoria della Relatività Generale .
Legge di conservazione della carica elettrica
Le radici della " conservazione della carica elettrica " risalgono a molto prima della scoperta dell’elettrone (la prima particella elementare, ancor oggi considerata come tale), avvenuta nel 1897 e della sua verifica al livello delle particelle elementari. Nel 1747 la singolare figura di scienziato e statista americano Benjamin Franklin (1706-1790) riconobbe esplicitamente che il "Fuoco elettrico" (così egli chiama la carica elettrica) è "non creato da attrito, ma solo raccolto". Egli scrisse:
“It is now discovered and demonstrated, both here and in Europe, that the Electrical Fire is a real Element, or Species of Matter, not created by the Friction, but collected only”.
E' ormai scoperto e dimostrato, sia qui che in Europa, che il Fuoco Elettrico è un vero e proprio elemento, o specie di Materia, non creato da strofinio, ma solo raccolto.
( Lettera a Cadwallader Colden, 5 giugno 1747 ; The Papers of Benjamin Franklin Vol. 3, Yale University Press, 1961) .
La conservazione della carica elettrica non è stata mai smentita sperimentalmente. In linguaggio scientifico, si può oggi dire che decadimenti dell’elettrone che la violino non sono stati osservati e, se esistono, avvengono con una vita media di oltre 10 24 anni. Parimenti, se il neutrone decade violando la conservazione della carica elettrica, questo avviene con una probabilità circa 10 26 volte inferiore a quella del suo normale modo di decadere in un protone, un elettrone e un neutrino con una vita media di circa 15 minuti (per quest'ultimo, vedete Interazione Elettro-Debole ).
Tramite il Teorema di Noether, nell'ambito della fisica classica la conservazione della carica elettrica deriva da una simmetria, e precisamente dall'invarianza delle leggi dell'elettromagnetismo - le Equazioni di Maxwell (vedete Interazione Elettromagnetica "alla Feynman" ) - rispetto a una " Trasformazione di Gauge " del potenziale elettromagnetico. La nuova parola non vi spaventi, come non si spaventano i bambini nell'affrontarne e tranquillamente impararne quotidianamente: una tale trasformazione è anologa alla ben nota possibilità di aggiungere una costante arbitraria al potenziale gravitazionale . Ne faremo presto una sua conoscenza più approfondita. Anche al livello fondamentale delle particelle elementari la conservazione della carica elettrica deriva da una simmetria, precisamente rispetto a una "Trasformazione di Gauge Globale".
La conservazione della carica elettrica acquista così un fondamento teorico e diventa "legge di conservazione", superando lo "stato sociale" di fatto empirico.
In particolare, la conservazione del numero barionico (finora) protegge la vita del protone, che non trova barioni di massa inferiore in cui decadere rispettando la legge di conservazione dell'energia (ivi compresa l'equivalente energetico della massa). Sperimentalmente si può solo dire che la sua vita media non è inferiore a 10 34 - 10 35 anni.
Concettualmente, la conservazione del numero barionico ci tocca direttamente, essendo la nostra massa corporea costituita di protoni e neutroni. Ma i numeri escludono ampiamente l'efficacia di una siffatta cura dimagrante senza dieta: ne abbiamo circa 5 x 10 28 e rischiamo di perderne uno solamente ogni milione di anni di una nostra ipotetica vita. Ma il vero scopo di questo esercizio è mostrare le difficoltà nella realizzare esperimenti che facciano luce sul decadimento del protone.
Tuttavia, vale decisamente la pena affrontarle perché l'interesse scientifico è di grandissimo rilievo. L'osservazione di un decadimento del protone aprirebbe la strada a un nuovo capitolo della Fisica, quale sarebbe una “ Grande Unificazione ” delle Interazioni Fondamentali. L’argomento è accennato in Interazione Elettro-Debole .
Fase: Luna, onda e funzione d'onda
Per prepararci a comprendere le già menzionate Trasformazioni di Gauge, chiariamo il concetto di "angolo di fase" (o semplicemente "fase"). Iniziamo pensando alla Luna. L'immagine che essa ci offre varia periodicamente, in altre parole oscilla. Parliamo qualitativamente delle sue fasi chiamandole Luna piena, tre quarti, mezza, un quarto e nuova.
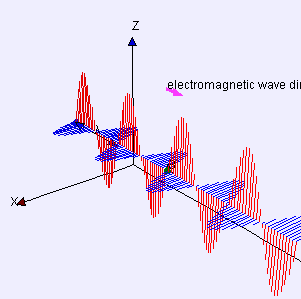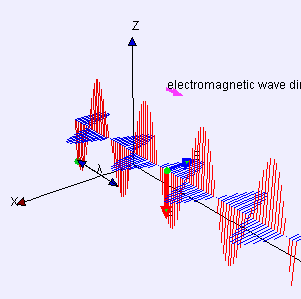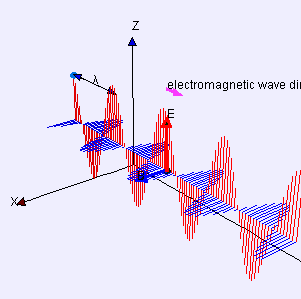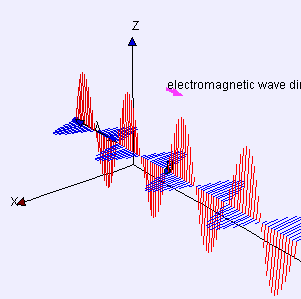
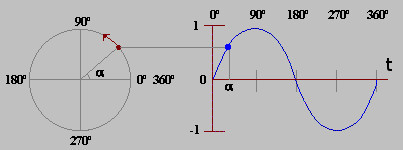
Consideriamo ora un'onda, per esempio quella elettromagnetica schematizzata in figura 10 (vedete Interazione Elettromagnetica "alla Feynman" ). Focalizziamo, per esempio, l'attenzione sul campo elettrico E, che in figura è rappresentato in rosso. Osservato in un dato punto in funzione del tempo, esso oscilla come mostrato in figura 11 a destra. Come per le fasi della Luna, potremmo qualitativamente parlare di onda piena, tre quarti e via dicendo. Come esprimere la fase in modo più preciso? La figura 11 a sinistra, combinata con quella a destra, mostra che immaginandola associata matematicamente a una rotazione possiamo darne un valore numerico quantitativo tramite un "angolo di fase", indicato con α in figura.
Per particelle elementari, dobbiamo parlare di "funzione d'onda" e di "ampiezza di probabilità", secondo concetti esposti in Onde e particelle per pedoni molto curiosi , ripresi in Interazione Elettromagnetica "alla Feynman" e sintetizzati in Appendice per vostra comodità. L'ampiezza di probabilità in funzione del tempo in un dato punto dello spazio è anch'essa caratterizzata da una fase, come un'onda. La fase è essenziale per caratterizzare la funzione d'onda in modo completo e descrivere compiutamente i fenomeni fisici. Tuttavia essa non influisce sulla "probabilità", che è data dal quadrato dell'ampiezza di probabilità: nell'operazione di quadratura la fase scompare.
Trasformazioni di Gauge Globale e Locali
Abbiamo già parlato di Trasformazioni di Gauge in relazione alla legge di conservazione della carica elettrica. L’appellativo " Gauge " (in italiano “taratura”, "calibrazione") deriva dalla loro caratteristica di modificare in modo controllato una specifica grandezza fisica in tutto il dominio dello spazio e del tempo (spazio-tempo in casi relativistici).
Per le particelle, la cosiddetta "Trasformazione di Gauge Globale" consiste nel modificare di una entità costante le fasi delle funzioni d'onda in tutto il dominio dello spazio-tempo, come delineato nell'articolo Il mistero della Simmetria nel citato numero della rivista Asimmetrie da cui sono estratte le figure 12 e 13.
La figura 12 rappresenta un'analogia a una Trasformazione di Gauge Globale. I singoli vasi rappresentati in figura hanno una perfetta simmetria rotazionale e i loro contenuti simboleggiano delle probabilità, che come detto sopra non dipendono dagli angoli di fase (simboleggiati da angoli di rotazione dei vasi). Una Trasformazione di Gauge Globale consiste nel cambiare tutte le fasi (ruotare tutti i vasi) di una stessa quantità, il che non altera le leggi fisiche: è come aggiungere una costante al potenziale gravitazionale della fisica classica.
La figura 13 mostra una simile analogia riferita a una ulteriore possibilità teoricamente offerta, le "Trasformazioni di Gauge Locali", che consistono nel modificare le fasi sempre in modo controllato (in accordo con la denominazione di gauge), ma variabile da punto a punto (da vaso a vaso). Esse alterano le leggi fisiche. Vedremo le grandissime sorprese a cui porta il trovare la cura per ristabilirle.
Dal Teorema di Noether verso la dinamica
Consideriamo per esempio la "fondamentale" legge di conservazione della quantità di moto e riflettiamo, con un poco di fantasia. Secondo il Teorema di Noether, essa deriva una simmetria. D'altra parte, sappiamo che essa regola la cinematica dei processi fisici e che la cinematica confina con la dinamica. E' assurdo pensare che richieste di simmetrie rispetto a trasformazioni specialmente concepite possano portare oltre il confine della cinematica e invadere il terreno delle leggi della dinamica, cioè a forze o in termini più precisi a "Interazioni Fondamentali"? In effetti, questo si può ottenere nella pratica attraverso l'imposizione di una invarianza rispetto a Trasformazioni di Gauge Locali, sopra definite in modo astratto.
Infine
Il Teorema di Noether potrebbe essere inizialmente apparso di interesse puramente speculativo, al pari dell'acquisita coscienza della natura fondamentale delle simmetrie manifestata nel portare alle leggi di conservazione. L'estensione del percorso alle leggi della dinamica e alle forze che vi intervengono ne dimostra il fortissimo interesse pratico e il valore culturale nel senso più vasto, secondo quanto detto nell'incipit.
Concludiamo con parole di Christopher Hill e Leon Lederman ( Premio Nobel 1988 ) in un loro saggio sulle simmetrie disponibile sul Web:
Aggiungiamo: non solo la legge di Newton.
Per approfondire
La rivista Asimmetrie ( numero 11, 2011 ) offre letture complementari attraverso articoli dedicati a Simmetrie e Asimmetrie nei loro diversi aspetti e attualità. La Fisica di Feynman (Simmetrie e leggi di conservazione, Cap. 52-3, Vol. 1) è sempre una lettura illuminante. Per letture a livello più avanzato, segnaliamo quanto segue.
Claudio Cereda, Simmetrie della Natura e Leggi di Conservazione
Christopher T. Hill e Leon M. Lederman, Teaching Symmetry in the Introductory Physics Curriculum , Fermi National Laboratory e Illinois Math and Science Academy (USA)
Herman Weyl, Symmetry - Simmetria ( pdf ), Princeton University Press - Feltrinelli (1952)
Onde e particelle per pedoni molto curiosi illustra il peculiare comportamento, secondo le circostanze, di quelle che nel linguaggio corrente chiamiamo particelle. In realtà esse sono onde "e" particelle, da trattare con le metodologie della Meccanica Quantistica ivi esposte e in Interazione Elettromagnetica “alla Feynman” . Sintetizziamole in poche parole.
La Legge di Coulomb esprime la forza elettrostatica esercitata su una carica unitaria in termini di un "campo" elettrico E. Con le Equazioni di Maxwell dell'elettromagnetismo classico, il campo diventa elettromagnetico e viene individuata l'esistenza delle onde elettromagnetiche, tra cui la luce. La rappresentazione schematica in figura 10 mostra che i campi elettrico E e magnetico B si propagano oscillando in direzioni ortogonali, e costanti se l'onda è "polarizzata" linearmente. Per un'illustrazione generale del concetto di campo, vedete il testo online Amaldi 2.0 .
Una particella è rappresentata da una "funzione d'onda" Ψ(x, y, z, t), che fornisce la "ampiezza di probabilità" che la particella si trovi in quello stato. La "probabilità" ne è il quadrato, il che assicura che sia sempre positiva. Esse corrispondono rispettivamente all'ampiezza e all'intensità mostrate in figura A1. La funzione d'onda rispetta il Principio di Indeterminazione . Se interpretata come riferentesi a una particella, la figura A1 corrisponde a una particella con lunghezza d'onda e quantità di moto perfettamente definite, ma con posizione totalmente indeterminata.
Le particelle della fisica classica sono entità localizzate nel tempo e nello spazio e il "punto materiale" ne è l'estrema idealizzazione, introdotta per scopi pratici nella comprensione delle leggi fisiche. I "quanti" della meccanica quantistica sono una estensione - con proprie leggi - di questo modo di vedere le entità elementari della materia. Pur essendo rappresentati da onde, alla scala macroscopica di un apparato sperimentale se ne osservano le tracce o se ne registrano i segnali "a colpo" come per particelle nel senso comune della parola.
.
..
Professore Emerito di Fisica Sperimentale
Università di Napoli "Federico II"
Complesso Univ. Monte S. Angelo
Via Cintia - 80126 Napoli - Italy
Simmetrie e Principi di conservazione è stato creato da P. Strolin
Simmetrie, leggi di conservazione e oltre
................
................
Per domande: autore o
Domanda a un esperto
Per illustrare la portata dell'argomento trattato in questo articolo nello sviluppo della cultura umana, iniziamo con le parole scritte da Hermann Weyl nella prefazione del suo libro Symmetry (1952) per chiarirne gli intenti:
"I aim at two things: On the one hand to clarify, step by step, the philosophic-mathematical significance of the idea of symmetry and, on the other, to display the great variety of applications of symmetry
in the arts, in inorganic and organic nature"
Io per scopo due cose: da un lato chiarire, passo dopo passo, l'importanza filosofica-matematica dell'idea di simmetria e, dall'altro, mostrare la grande varietà di applicazioni della simmetria nelle arti, nella natura inorganica e in quella organica.
in the arts, in inorganic and organic nature"
Io per scopo due cose: da un lato chiarire, passo dopo passo, l'importanza filosofica-matematica dell'idea di simmetria e, dall'altro, mostrare la grande varietà di applicazioni della simmetria nelle arti, nella natura inorganica e in quella organica.
|
Fig. 1. La simmetria del cerchio megalitico di Stonehenge in un acquarello di Lucas de Heere (circa 1568) Manoscritto Add MS 28330 , British Library (Londra) Immagine British Library - Clic per pagina completa in originale | ..... |
Esprimiamo in altre parole e portiamo ai nostri tempi lo spirito di Hermann Weyl. La simmetria si manifesta anche visivamente in Natura e da tempi antichissimi è presente nella cultura umana: vedete, per esempio, il misterioso cerchio megalitico di Stonehenge rappresentato in figura 1 da una preziosa testimonianza. La Fisica ha portato a capire che la simmetria è anche radice profonda della struttura del mondo che ci circonda al livello più fondamentale - quello delle particelle elementari - e delle forze che la determinano: lo mostra la figura 2. Tutto poggia su simmetrie.
Questo mostra che, al suo livello più alto, Fisica è Cultura nel senso più largo del termine. In una sintesi complessiva, lo sforzo di assorbire intellettualmente concetti e aspetti tecnici di questo articolo e di Simmetrie e Interazioni Fondamentali vi premierà con la soddisfazione di rendervene concretamente conto.
Il tracciato dell'articolo
La figura 3 dipinge in forma scherzosa un evento della vita di tutti i giorni, che accade al momento del talvolta doloroso risveglio e che, con un poco di fantasia, possiamo interpretare come un effetto della legge di conservazione della quantità di moto , nel caso particolare di corpo in quiete.
| ......................................................................................................
Fig. 3. Un oggetto a riposo tende a rimanere a riposo (specialmente il sabato mattina)
Immagine Doodlegirls - Spectrum | ..... | ............................................. Nei libri di fisica classica, la legge di conservazione della quantità di moto viene definita "principio", sottintendendo che essa è praticamente assurta al livello di "credo" ed esentata dal subire sempre più precise verifiche sperimentali. Lo stesso privilegio è condiviso dalla conservazione energia e da quella del momento angolare (o della quantità di moto). Le altre restano leggi di carattere empirico e senza certezza di validità assoluta. |
In quest'articolo illustriamo un fondamentale sviluppo del pensiero scientifico avvenuto all'inizio del Novecento, con l'avvento della cosiddetta fisica moderna: il " Teorema di Noether ", secondo il quale a ogni legge di conservazione corrisponde una simmetria e viceversa.
Con il Teorema di Noether, a livello profondo le "leggi di conservazione" classicamente regnanti assolute con la denominazione "principi" si trovano deducibili da una simmetria, e "conservazioni" considerate empiriche salgono in nobiltà al livello di "leggi" grazie a una simmetria che le sostiene. E questo non solo nell'ambito della fisica classica, ma anche nel mondo quantistico fino al livello fondamentale delle particelle elementari.
Inizieremo a vedere che - partendo dal Teorema di Noether - le simmetrie permettono di andare anche oltre verso aspetti dinamici e giungono a manifestarsi come fondamento di una nuova visione delle Interazioni Fondamentali, esposta in Simmetrie e Interazioni Fondamentali . Ne sono strumento le simmetrie rispetto alle cosiddette "Trasformazioni di Gauge" e in particolare quelle dette "Locali". Le introdurremo.
Leggi di conservazione
Cosa hanno in comune le figure 4 e 5, pur su scale dimensionali incomparabili? Andiamo in bicicletta senza pensare che non cadiamo grazie alla " legge di conservazione del momento angolare " nel moto di rotazione delle ruote (figura 4), che agiscono come un giroscopio . Guardiamo il cielo e non pensiamo che la stessa legge regola il moto dei corpi celesti, per esempio la rotazione delle stelle in una galassia (figura 5).
|
Fig. 4. John Lennon , del gruppo dei Beatles , protagonisti della rivoluzione nella musica e nel costume negli anni '60 Immagine www.ilpost.it | ..... |
Leggi di conservazione come quella del momento angolare hanno carattere generale e fondamentale. Secoli di pensiero scientifico hanno portato alla loro concezione da parte di giganti scientifici quali Cartesio, Newton e Huygens.
| ..... |
Fig. 7. I barioni con spin J = ½ costituiti di quarks down, up, strano e charm Immagine SELEX experiment - Fermilab |
Simmetrie
Due immagini sintetizzano simbolicamente la fondamentale importanza delle simmetrie nella struttura del mondo organico e inorganico. In figura 6 vedete l' Uomo Vitruviano " nel famoso disegno di Leonardo da Vinci (1452-1519), databile al 1490 circa e conservato alle Gallerie dell'Accademia a Venezia. La figura 7 mostra la struttura dei barioni con spin J = ½ costituiti di quarks down, up, strano e charm nel Modello a quarks e offre un esempio dell'importanza delle Simmetrie nella fisica moderna (vedete e Simmetrie: protoni, neutroni e ... quarks ).
Teorema di Noether
Tra il 1915 e il 1918 Emmy Noether pose una fondamentale pietra miliare della Scienza dimostrando che - in linea generale - le leggi di conservazione sono legate a simmetrie ossia a invarianze rispetto a trasformazioni, per quanto detto in Simmetrie: dai solidi platonici alla struttura cristallina . Più precisamente esso afferma che a ogni simmetria delle leggi fisiche per una trasformazione di tipo continuo corrisponde una grandezza fisica conservata, cioè un legge di conservazione. E viceversa a ogni grandezza fisica conservata corrisponde una simmetria.
Il "Teorema di Noether" fu praticamente ignorato per mezzo secolo. Lo fu la stessa Emmy Noether, salvo che in ristretti ambienti scientifici. Ma la portata pratica del suo teorema è vasta e profonda.
Anzitutto, stabilendo in modo formale una diretta connessione tra leggi di conservazione e simmetrie - ambedue fondamentali - diventa il loro "anello di congiunzione". Le leggi di conservazione non appaiono più necessariamente come "principi" nel senso letterale della parola e escono dall'originario isolamento assiomatico. Questo aspetto è discusso nel presente articolo. Simmetrie e Interazioni Fondamentali ne estende il discorso e giunge a individuare nelle simmetrie il fondamento teorico delle Interazioni Fondamentali. Oggi le simmetrie appaiono quindi essere la base del livello più profondo della conoscenza. Guardate di nuovo la bella immagine di Stonehenge in figura 1 - il nostro punto di partenza - per rendervi conto del progresso fatto dalla cultura umana.
| .................................................................... | ... | ............................................. Emmy Noether La figura 8 mostra l’illustre donna di Scienza Emmy (Amalie) Noether (1882-1935), con il suo sguardo speciale. Emmy Noether fu un genio della matematica, pur se non nota quanto Marie Curie per la Fisica. Albert Einstein disse di lei in un intervento sul New York Times in occasione della sua scomparsa:
"In the judgement of the most competent living mathematicians, Fräulein Noether was the most significant creative mathematical genius thus far produced since the higher education of women began"
Secondo il giudizio dei matematici contemporanei più competenti, la Signorina Noether è stata il più importante e creativo genio matematico finora prodotto da quando le donne hanno avuto accesso all'istruzione superiore. ( New York Times, 3 maggio 1935 ) Se siete incuriositi dalla personalità di Emmy Noether, leggete Emmy Noether, simmetrie e leggi di conservazione sulla rivista Asimmetrie, Genio matematico e trasandato su Galileo o una sua brevissima biografia sul sito della Association for Women in Mathematics. |
Leggi di conservazione dell'energia, della quantità di moto e del momento angolare
Vediamo il messaggio dato dal Teorema di Noether in relazione alle trasformazioni spaziali e temporali: la legge di conservazione dell'energia deriva da una simmetria delle leggi fisiche rispetto a una traslazione temporale, quella della quantità di moto da una rispetto a una traslazione spaziale e quello del momento angolare da una rispetto a una rotazione spaziale.
In altre parole, l'energia non fosse conservata le leggi fisiche non sarebbero invarianti nel tempo. Analogamente per quantità di moto e traslazione spaziale, al pari di momento angolare e rotazione spaziale. In pratica, le simmetrie assicurano che le leggi fisiche abbiano validità universale e perenne. Oltretutto, se così non fosse sarebbe un gran disastro. E' una riprova della natura assolutamente fondamentale delle simmetrie.
Con un grande balzo in avanti, il Teorema di Noether si ricollega alle origini della Scienza moderna e cioè alla questione generale dell'Invarianza delle leggi fisiche, che è alla base della Relatività Galileiana e della Teoria della Relatività Speciale di Einstein come discusso in Simmetrie e Relatività Speciale e diviene postulato fondamentale nella Teoria della Relatività Generale .
Legge di conservazione della carica elettrica
Le radici della " conservazione della carica elettrica " risalgono a molto prima della scoperta dell’elettrone (la prima particella elementare, ancor oggi considerata come tale), avvenuta nel 1897 e della sua verifica al livello delle particelle elementari. Nel 1747 la singolare figura di scienziato e statista americano Benjamin Franklin (1706-1790) riconobbe esplicitamente che il "Fuoco elettrico" (così egli chiama la carica elettrica) è "non creato da attrito, ma solo raccolto". Egli scrisse:
“It is now discovered and demonstrated, both here and in Europe, that the Electrical Fire is a real Element, or Species of Matter, not created by the Friction, but collected only”.
E' ormai scoperto e dimostrato, sia qui che in Europa, che il Fuoco Elettrico è un vero e proprio elemento, o specie di Materia, non creato da strofinio, ma solo raccolto.
( Lettera a Cadwallader Colden, 5 giugno 1747 ; The Papers of Benjamin Franklin Vol. 3, Yale University Press, 1961) .
La conservazione della carica elettrica non è stata mai smentita sperimentalmente. In linguaggio scientifico, si può oggi dire che decadimenti dell’elettrone che la violino non sono stati osservati e, se esistono, avvengono con una vita media di oltre 10 24 anni. Parimenti, se il neutrone decade violando la conservazione della carica elettrica, questo avviene con una probabilità circa 10 26 volte inferiore a quella del suo normale modo di decadere in un protone, un elettrone e un neutrino con una vita media di circa 15 minuti (per quest'ultimo, vedete Interazione Elettro-Debole ).
Tramite il Teorema di Noether, nell'ambito della fisica classica la conservazione della carica elettrica deriva da una simmetria, e precisamente dall'invarianza delle leggi dell'elettromagnetismo - le Equazioni di Maxwell (vedete Interazione Elettromagnetica "alla Feynman" ) - rispetto a una " Trasformazione di Gauge " del potenziale elettromagnetico. La nuova parola non vi spaventi, come non si spaventano i bambini nell'affrontarne e tranquillamente impararne quotidianamente: una tale trasformazione è anologa alla ben nota possibilità di aggiungere una costante arbitraria al potenziale gravitazionale . Ne faremo presto una sua conoscenza più approfondita. Anche al livello fondamentale delle particelle elementari la conservazione della carica elettrica deriva da una simmetria, precisamente rispetto a una "Trasformazione di Gauge Globale".
La conservazione della carica elettrica acquista così un fondamento teorico e diventa "legge di conservazione", superando lo "stato sociale" di fatto empirico.
| .............................................................................
Fig. 9. Sorprese della vita Francesco Tullio Altan - Immagine Finanza Online | ... | ............................................. Conservazioni empiriche Diverso da quelli trattati sopra è il caso delle "conservazioni" che poggiano solamente sulla attuale inesistenza di osservazioni che le smentiscano: le sorprese sono sempre possibili, interessanti e potenzialmente molto belle. Nulla a che vedere con altre sorprese, come quella mostrata in figura 9. Esempi ormai storici di conservazioni poi smentite da fatti sperimentali sono la "conservazione della Parità" e la “conservazione della Simmetria CP”, delle quali trattano Asimmetrie: violazione della Parità e neutrino allo specchio , Asimmetrie: come fu scoperta la violazione della Parità e Asimmetrie: CP, tempo e antimateria scomparsa . Guardando ai misteri ancora aperti, di grande rilevanza è la cosiddetta “ conservazione del numero barionico ”, secondo la quale in un qualsiasi processo fisico resta invariato il numero di barioni, ossia delle particelle della famiglia del protone e del neutrone (vedete Protone, pione & adroni ). |
In particolare, la conservazione del numero barionico (finora) protegge la vita del protone, che non trova barioni di massa inferiore in cui decadere rispettando la legge di conservazione dell'energia (ivi compresa l'equivalente energetico della massa). Sperimentalmente si può solo dire che la sua vita media non è inferiore a 10 34 - 10 35 anni.
Concettualmente, la conservazione del numero barionico ci tocca direttamente, essendo la nostra massa corporea costituita di protoni e neutroni. Ma i numeri escludono ampiamente l'efficacia di una siffatta cura dimagrante senza dieta: ne abbiamo circa 5 x 10 28 e rischiamo di perderne uno solamente ogni milione di anni di una nostra ipotetica vita. Ma il vero scopo di questo esercizio è mostrare le difficoltà nella realizzare esperimenti che facciano luce sul decadimento del protone.
Tuttavia, vale decisamente la pena affrontarle perché l'interesse scientifico è di grandissimo rilievo. L'osservazione di un decadimento del protone aprirebbe la strada a un nuovo capitolo della Fisica, quale sarebbe una “ Grande Unificazione ” delle Interazioni Fondamentali. L’argomento è accennato in Interazione Elettro-Debole .
Fase: Luna, onda e funzione d'onda
Per prepararci a comprendere le già menzionate Trasformazioni di Gauge, chiariamo il concetto di "angolo di fase" (o semplicemente "fase"). Iniziamo pensando alla Luna. L'immagine che essa ci offre varia periodicamente, in altre parole oscilla. Parliamo qualitativamente delle sue fasi chiamandole Luna piena, tre quarti, mezza, un quarto e nuova.
Consideriamo ora un'onda, per esempio quella elettromagnetica schematizzata in figura 10 (vedete Interazione Elettromagnetica "alla Feynman" ). Focalizziamo, per esempio, l'attenzione sul campo elettrico E, che in figura è rappresentato in rosso. Osservato in un dato punto in funzione del tempo, esso oscilla come mostrato in figura 11 a destra. Come per le fasi della Luna, potremmo qualitativamente parlare di onda piena, tre quarti e via dicendo. Come esprimere la fase in modo più preciso? La figura 11 a sinistra, combinata con quella a destra, mostra che immaginandola associata matematicamente a una rotazione possiamo darne un valore numerico quantitativo tramite un "angolo di fase", indicato con α in figura.
| ............................................. | ... | ...................... ................ Fig. 11. La fase di un'onda A destra: l'oscillazione in un dato punto in funzione del tempo t, per un'onda di ampiezza unitaria A sinistra: la fase dell'onda al tempo t, espressa tramite un angolo di fase α: l'oscillazione mostrata a destra può essere vista come la proiezione del moto rotatorio sull'asse verticale. Immagine Augustin Borrego Colomer |
Per particelle elementari, dobbiamo parlare di "funzione d'onda" e di "ampiezza di probabilità", secondo concetti esposti in Onde e particelle per pedoni molto curiosi , ripresi in Interazione Elettromagnetica "alla Feynman" e sintetizzati in Appendice per vostra comodità. L'ampiezza di probabilità in funzione del tempo in un dato punto dello spazio è anch'essa caratterizzata da una fase, come un'onda. La fase è essenziale per caratterizzare la funzione d'onda in modo completo e descrivere compiutamente i fenomeni fisici. Tuttavia essa non influisce sulla "probabilità", che è data dal quadrato dell'ampiezza di probabilità: nell'operazione di quadratura la fase scompare.
Trasformazioni di Gauge Globale e Locali
Abbiamo già parlato di Trasformazioni di Gauge in relazione alla legge di conservazione della carica elettrica. L’appellativo " Gauge " (in italiano “taratura”, "calibrazione") deriva dalla loro caratteristica di modificare in modo controllato una specifica grandezza fisica in tutto il dominio dello spazio e del tempo (spazio-tempo in casi relativistici).
Per le particelle, la cosiddetta "Trasformazione di Gauge Globale" consiste nel modificare di una entità costante le fasi delle funzioni d'onda in tutto il dominio dello spazio-tempo, come delineato nell'articolo Il mistero della Simmetria nel citato numero della rivista Asimmetrie da cui sono estratte le figure 12 e 13.
| .............................................
Fig. 12. Analogia a una Trasformazione di Gauge Globale Immagine A. Masiero e M. Petroni - Asimmetrie | ... | ......................
Fig. 13. Analogia a una Trasformazione di Gauge Locale Immagine A. Masiero e M. Petroni - Asimmetrie |
La figura 12 rappresenta un'analogia a una Trasformazione di Gauge Globale. I singoli vasi rappresentati in figura hanno una perfetta simmetria rotazionale e i loro contenuti simboleggiano delle probabilità, che come detto sopra non dipendono dagli angoli di fase (simboleggiati da angoli di rotazione dei vasi). Una Trasformazione di Gauge Globale consiste nel cambiare tutte le fasi (ruotare tutti i vasi) di una stessa quantità, il che non altera le leggi fisiche: è come aggiungere una costante al potenziale gravitazionale della fisica classica.
La figura 13 mostra una simile analogia riferita a una ulteriore possibilità teoricamente offerta, le "Trasformazioni di Gauge Locali", che consistono nel modificare le fasi sempre in modo controllato (in accordo con la denominazione di gauge), ma variabile da punto a punto (da vaso a vaso). Esse alterano le leggi fisiche. Vedremo le grandissime sorprese a cui porta il trovare la cura per ristabilirle.
Dal Teorema di Noether verso la dinamica
Consideriamo per esempio la "fondamentale" legge di conservazione della quantità di moto e riflettiamo, con un poco di fantasia. Secondo il Teorema di Noether, essa deriva una simmetria. D'altra parte, sappiamo che essa regola la cinematica dei processi fisici e che la cinematica confina con la dinamica. E' assurdo pensare che richieste di simmetrie rispetto a trasformazioni specialmente concepite possano portare oltre il confine della cinematica e invadere il terreno delle leggi della dinamica, cioè a forze o in termini più precisi a "Interazioni Fondamentali"? In effetti, questo si può ottenere nella pratica attraverso l'imposizione di una invarianza rispetto a Trasformazioni di Gauge Locali, sopra definite in modo astratto.
| .............................................................................
Fig. 14. Manifesto pubblicitario del film Sulle orme della pantera rosa - Immagine Wikipedia | .... | ...................... Itinerario oltre confine Consideriamo la legge fisica di una particella libera e applichiamo una ben pensata Trasformazioni di Gauge Locale: la sua simmetria è distrutta. Per ristabilirla e sistemare la situazione diventa necessario "inventare" qualcosa: una specifica "interazione" corrispondente alla trasformazione applicata. E introdurla nella legge fisica per la particella libera. Le cosiddette "Teorie di Gauge" delle Interazioni Fondamentali sono costruite così, deducendole dall'imposizione di specifiche simmetrie rispetto a Trasformazioni di Gauge Locali concepite teoricamente in base alla fenomenologia dei dati sperimentali. Tutto nasce da simmetrie. Una interazione così scoperta - o teoricamente ritrovata, se già conosciuta - è formalmente definita su basi teoriche. L'interazione risulta avere caratteristiche strettamente associate alla Trasformazione di Gauge Locale giudiziosamente applicata. Le osservazioni sperimentali contribuiscono a a guidare la scelta della opportuna trasformazione e devono poi necessariamente validare le predizioni della teoria. Fa qualcosa del genere l'Ispettore Clouseau per la ricerca della pantera rosa individuando attentamente le sue orme, nel film Sulle orme della pantera rosa (figura 14). Il percorso continua in Simmetrie e Interazioni Fondamentali : vivedete come nascono le attuali Teorie di Gauge della Interazione Elettro-Debole e della Interazione Forte, fenomenologicamente descritte in Interazione Elettro-Debole e in Interazione Forte . |
Infine
Il Teorema di Noether potrebbe essere inizialmente apparso di interesse puramente speculativo, al pari dell'acquisita coscienza della natura fondamentale delle simmetrie manifestata nel portare alle leggi di conservazione. L'estensione del percorso alle leggi della dinamica e alle forze che vi intervengono ne dimostra il fortissimo interesse pratico e il valore culturale nel senso più vasto, secondo quanto detto nell'incipit.
Concludiamo con parole di Christopher Hill e Leon Lederman ( Premio Nobel 1988 ) in un loro saggio sulle simmetrie disponibile sul Web:
"Conservation laws, like the conservation of energy, momentum and angular momentum (these are the most famous), are studied in high school. We now see from Noether's theorem that they emerge from symmetry concepts far deeper than Newton's laws"
Le leggi di conservazione, come la conservazione dell'energia, della quantità di moto e del momento angolare (questi sono i più famosi), si studiano al liceo. Ora vediamo dal teorema di Noether che esse emergono da concetti di simmetria di gran lunga più profondi delle leggi di Newton.
C.T. Hill e L.M. Lederman, Teaching Symmetry in the Introductory Physics Curriculum
Le leggi di conservazione, come la conservazione dell'energia, della quantità di moto e del momento angolare (questi sono i più famosi), si studiano al liceo. Ora vediamo dal teorema di Noether che esse emergono da concetti di simmetria di gran lunga più profondi delle leggi di Newton.
C.T. Hill e L.M. Lederman, Teaching Symmetry in the Introductory Physics Curriculum
Aggiungiamo: non solo la legge di Newton.
Per approfondire
La rivista Asimmetrie ( numero 11, 2011 ) offre letture complementari attraverso articoli dedicati a Simmetrie e Asimmetrie nei loro diversi aspetti e attualità. La Fisica di Feynman (Simmetrie e leggi di conservazione, Cap. 52-3, Vol. 1) è sempre una lettura illuminante. Per letture a livello più avanzato, segnaliamo quanto segue.
Claudio Cereda, Simmetrie della Natura e Leggi di Conservazione
Christopher T. Hill e Leon M. Lederman, Teaching Symmetry in the Introductory Physics Curriculum , Fermi National Laboratory e Illinois Math and Science Academy (USA)
Herman Weyl, Symmetry - Simmetria ( pdf ), Princeton University Press - Feltrinelli (1952)
APPENDICE
Campi, onde e particelle
Campi, onde e particelle
Onde e particelle per pedoni molto curiosi illustra il peculiare comportamento, secondo le circostanze, di quelle che nel linguaggio corrente chiamiamo particelle. In realtà esse sono onde "e" particelle, da trattare con le metodologie della Meccanica Quantistica ivi esposte e in Interazione Elettromagnetica “alla Feynman” . Sintetizziamole in poche parole.
La Legge di Coulomb esprime la forza elettrostatica esercitata su una carica unitaria in termini di un "campo" elettrico E. Con le Equazioni di Maxwell dell'elettromagnetismo classico, il campo diventa elettromagnetico e viene individuata l'esistenza delle onde elettromagnetiche, tra cui la luce. La rappresentazione schematica in figura 10 mostra che i campi elettrico E e magnetico B si propagano oscillando in direzioni ortogonali, e costanti se l'onda è "polarizzata" linearmente. Per un'illustrazione generale del concetto di campo, vedete il testo online Amaldi 2.0 .
| ............................................................................................................
Fig. A1. Ampiezza e intensità di un'onda
Immagine School Physics | ..... | ............................................................................... La figura A1 mostra la "ampiezza" e la "intensità" della oscillazione provocata da un'onda generica, in un dato punto dello spazio e in funzione del tempo. L'intensità (sempre positiva) di un'onda è proporzionale al quadrato della sua ampiezza (oscillante). Con l' ipotesi di de Broglie , alle particelle viene riconosciuto un comportamento quantistico-ondulatorio e sono anch'esse descritte da un "campo". Alle onde elettromagnetiche (compresa la luce) corrispondono particelle (o "quanti") dette “ fotoni ”. |
Una particella è rappresentata da una "funzione d'onda" Ψ(x, y, z, t), che fornisce la "ampiezza di probabilità" che la particella si trovi in quello stato. La "probabilità" ne è il quadrato, il che assicura che sia sempre positiva. Esse corrispondono rispettivamente all'ampiezza e all'intensità mostrate in figura A1. La funzione d'onda rispetta il Principio di Indeterminazione . Se interpretata come riferentesi a una particella, la figura A1 corrisponde a una particella con lunghezza d'onda e quantità di moto perfettamente definite, ma con posizione totalmente indeterminata.
Le particelle della fisica classica sono entità localizzate nel tempo e nello spazio e il "punto materiale" ne è l'estrema idealizzazione, introdotta per scopi pratici nella comprensione delle leggi fisiche. I "quanti" della meccanica quantistica sono una estensione - con proprie leggi - di questo modo di vedere le entità elementari della materia. Pur essendo rappresentati da onde, alla scala macroscopica di un apparato sperimentale se ne osservano le tracce o se ne registrano i segnali "a colpo" come per particelle nel senso comune della parola.
Paolo Strolin
.
..
Professore Emerito di Fisica Sperimentale
Università di Napoli "Federico II"
Complesso Univ. Monte S. Angelo
Via Cintia - 80126 Napoli - Italy
Ultima Modifica 9 Anni 2 Settimane fa da Paolo.
Si prega Accesso a partecipare alla conversazione.
Tempo creazione pagina: 0.668 secondi