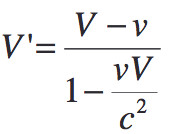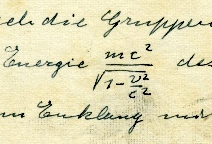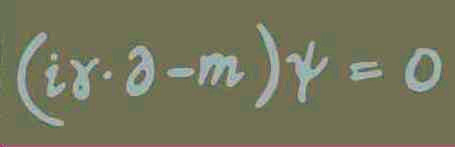Simmetrie e Relatività Speciale
- P. Strolin
-
Autore della discussione
- Offline
- Premium Utente
-
Less
Di più
12 Anni 7 Mesi fa - 9 Anni 2 Settimane fa #82
da P. Strolin
Partendo dalla Relatività galileiana, proseguiremo con la costanza della velocità della luce nelle Equazioni di Maxwell e l'esperimento di Michelson-Morley. Giungeremo infine alla Trasformazione di Lorentz e alla Teoria della Relatività nella sua formulazione più semplice, detta Speciale o Ristretta e limitata a un moto relativo uniforme.
Invarianza e simmetria
La "simmetria" di un cristallo consiste in una "invarianza" rispetto a specifiche rotazioni del cristallo stesso. In generale, vi è uno strettissimo legame tra i concetti di invarianza e di simmetria, evidenziato in Simmetrie: dai solidi platonici ai cristalli minerali . Volendo essere assolutamente precisi nel linguaggio, in Fisica si parla di "invarianza" di una grandezza fisica e di "covarianza" della formulazione di una legge fisica rispetto al sistema di riferimento. Per semplicità, concentreremo questi due concetti in uno e parleremo solo di invarianza.
La simmetria che porta alla Relatività consiste nell'invarianza delle leggi fisiche rispetto a trasformazioni di coordinate tra due sistemi in moto relativo uno rispetto all'altro.
Relatività galileiana
Galileo Galilei fu grande scienziato e grande comunicatore della Scienza, come gli era vitale al fine di convincere la Chiesa che stando sulla Terra non possiamo percepire il suo moto attorno al Sole. Nella seconda giornata del Dialogo sopra i due massimi sistemi del mondo (pubblicazione autorizzata nel 1632, vedetene il frontespizio in figura 2), Salviati - difensore della teoria copernicana - dice:
ché (pur di moto uniforme e non fluttuante in qua e in là) voi non riconoscerete una minima mutazione in tutti li nominati effetti; né da alcuno di quelli potrete comprendere se la nave cammina, o pure sta ferma".
Il discorso vale anche per l’astronauta di oggi nel suo astro-navilio, pur se non ha pescetti o farfalle. Notate come Galileo esprime la “Invarianza” delle leggi della Meccanica: per sistemi in moto lineare e uniforme ("non fluttuante") uno rispetto all'altro:
................
La “Relatività Galileiana" è figlia dell'Invarianza osservata nel navilio ed è collegata alla ben nota ta “trasformazione galileiana” delle coordinate spaziali x-y-z, con il tempo t che scorre autonomamente oltre che in modo inarrestabile. Essa implica un'addizione algebrica delle velocità: dati due sistemi di riferimento F' e F, la velocità V' di un corpo in F' è data dalla velocità V in F meno la velocità v di F' relativamente F, cioè per un moto lungo l'asse x:
................
La trasformazione galileiana assicura l'Invarianza delle leggi fisiche a lui note, e in particolare F = ma.
................
La luce non si cura del sistema di riferimento
Nel 1864 James Clerk Maxwell unificò fenomeni elettrici e magnetici formulando le leggi dell'elettro-magnetismo mediante le sue famose equazioni, come è delineato nell'articolo Interazioni elettro-magnetiche "alla Fenyman" . Esse dicono che nel vuoto le onde elettro-magnetiche, la luce in primis, si propagano tutte e sempre con la stessa velocità c e hanno quindi l'Invarianza "costruita dentro".
Secondo Maxwell, la luce non si cura della relatività galileiana, che prevede l'addizione di velocità. Anzi la relatività galileiana porterebbe a problemi: definita la velocità della luce in un sistema di riferimento, essa potrebbe esserne superiore in un'altro. Fu grande mistero, e grande finestra aperta sul futuro.
Nel 1887 l'esperimento di Michelson-Morley, del quale ci accingiamo a parlare, mostrò sperimentalmente che effettivamente la luce non si cura della velocità con cui ci muoviamo nello spazio assieme alla Terra. Non vi è bisogno di immaginare un ipotetico " etere " per cui valgano le Equazioni di Maxwell. La loro Invarianza, e assieme a essa quella della velocità della luce, fu anche realtà sperimentale da rispettare:
................
Esperimento di Michelson-Morley
I fenomeni di interferenza – caratteristici della natura ondulatoria - possono essere efficacemente utilizzati misurare con precisione la velocità della luce, come onda elettromagnetica.
Albert Michelson iniziò nel 1881 le sue famose misure sulla velocità della luce, completate nel 1887 mediante l’ interferometro da lui costruito assieme a Edward Morley. Come si è detto, nel 1864 dalle Equazioni di Maxwell la velocità della luce era sorprendentemente emersa come una costante. Le Equazioni di Maxwell dovevano considerarsi valide nel sistema di riferimento di un ipotetico “etere”? Se così fosse, l’addizione galileiana delle velocità della luce e della Terra rispetto all’etere avrebbe dovuto manifestarsi in velocità diverse secondo due direzioni ortogonali. Michelson confutò questa ipotesi, confrontando la velocità della luce nei due bracci ortogonali di un “interferometro”. Egli mostrò che la velocità della luce è la stessa nei due bracci, con un errore abbastanza piccolo da escludere un'addizione galileiana di velocità. Michelson ebbe il Premio Nobel 1907 .
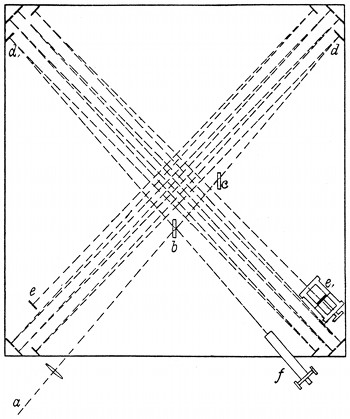
Le figure 3a e 3b, tratte dalla pubblicazione originale mostrano l’apparato sperimentale e lo schema dell’ottica. Una stessa sorgente (a) invia luce bianca in due bracci ortogonali lunghi poco più di un metro, tra i quali è suddivisa tramite uno specchio semi-riflettente (b). Una lastrina di vetro è inserita nel braccio ove la luce non attraversa lo specchio, per equalizzare la lunghezza dei percorsi della luce nei due bracci. La luce è quindi riflessa (d, e) e ricombinata prima di giungere al rivelatore (f), ove è osservata l'interferenza tra la luce in un braccio e quella nell'altro. La lunghezza efficace di ciascun braccio è estesa a 11 m tramite 8 riflessioni, al fine di amplificare il percorso della luce e la sensibilità della misura.
La figura 4 mostra l’interferometro nel sistema di riferimento dell’ipotetico etere, nel caso di moto di traslazione orizzontale dell’interferometro rispetto ad esso. Alla fine del suo viaggio di ritorno, la luce nel braccio verticale avrebbe trovato lo specchio spostato e, quindi, la necessità di percorrere una distanza maggiore, come schematicamente mostrato.
La figura 5 mostra le frange di interferenza in un interferometro come quello di Michelson-Morley. Notate il deterioramento della misura introdotto dall’effetto di dispersione cromatica , legato all’uso della luce "bianca" emessa dal Sole, con tutte le sue componenti spettrali .
L’interferometro poteva essere ruotato, al fine di paragonare la velocità della luce in direzioni ortogonali. Esso era montato su un blocco di pietra con 1,5 m di lato e isolato al meglio dalle vibrazioni, altrimenti:
“it was impossible to see the interference fringes except at brief intervals when working in the city, even at two o'clock in the morning”
(lavorando in città era impossibile vedere le frange di interferenza tranne che a brevi intervalli, anche alle due del mattino).
Gli autori stimavano di avere un limite di sensibilità pari a 1/100 della larghezza delle frange. Non fu osservato alcun effetto compatibile con una diversa velocità della luce nei due bracci per addizione galileiana di velocità.
Notate che l'interferometro di Michelson e Morley ha dato concettualmente origine agli attuali "Interferometri Laser" per l'osservazione di "Onde gravitazionali" (vedete Onde gravitazionali dall'oceano cosmico e Onde gravitazionali e laser: Einstein & Einstein )
Trasformazione di Lorentz
Dall'esigenza - teorica con le Equazioni di Maxwell e sperimentale con l'esperimento di Michelson e Morley - di rispettare l'Invarianza della velocità della luce scaturì nell’ultimo decennio dell’Ottocento la " trasformazione di Lorentz ". La denominazione fu data da Poincaré, che nel 1905 la pose nella forma attuale.
Come quella galileiana, la trasformazione di Lorentz si applica a sistemi in moto rettilineo e uniforme uno relativamente all’altro. Essa è mostrata schematicamente in figura 6, per un sistema F’ che si muove con velocità costante v lungo l’asse x rispetto al sistema F.
Iniziamo con una riflessione sul concetto di "contemporaneità" per segnali provenienti da sistemi in moto relativo. Per una velocità infinita di propagazione dei segnali, si può anche impunemente pensarla come riferita agli istanti di emissione. La velocità finita della luce c fornisce il limite di quella di propagazione dei segnali e impone un totale rigore logico: la contemporaneità non può che essere riferita al sistema e agli istanti in cui i segnali vengono osservati, come schematizzato dalla stella in figura.
Ne consegue che il tempo non è più un’entità assoluta e indipendente dallo spazio come per Galileo, ma dipende dal moto del sistema a cui si riferisce. I fenomeni devono essere visti in uno “spazio-tempo” e non più nello spazio "e" nel tempo. Entriamo in un nuovo mondo a quattro dimensioni (4D, secondo il dire usuale), con le tre dimensioni spaziali inseparabili da quella temporale: una rivoluzione del pensiero scientifico e filosofico.
Le coordinate spazio-temporali (x’, y', z’, t’) nel sistema F’ sono legate a quelle (x, y, z, t) nel sistema F dalla relazione indicata nell’inserto a fumetto in figura 6. Il fondamentale "fattore di Lorentz" γ è dato a destra in figura ed è funzione del rapporto v/c.
La pura addizione galileiana delle velocità è sostituita dalla relazione:
................
ove V e V’ sono le velocità nei due sistemi di riferimento. Per V = c si ha anche V' = c : la velocità v del sistema F’ rispetto a F non aggiunge o toglie nulla e l’invarianza della velocità della luce c è rispettata.
Per velocità v trascurabili rispetto a quella della luce c, il fattore di Lorentz γ vale 1 e si ritrova la trasformazione galileiana
................
con il tempo identico nei due sistemi. La trasformazione di Lorentz ha carattere più generale di quella galileiana, che resta un’approssimazione valida nel suo dominio. La Scienza avanza innovando senza smentirsi.
Contrazione spaziale e dilatazione temporale
Il fattore di Lorentz, che aumenta al crescere del rapporto v/c, porta una contrazione delle lunghezze nel sistema F' viste in F. E' la cosiddetta “contrazione di Lorentz”, mostrata schematicamente in figura 6. Ma è più divertente prendere alla lettera la sua denominazione, secondo un'idea tratta da Spacetime . La figura 7 a sinistra mostra Hendrik Lorentz (1853-1928) nel sistema di riferimento F’ in cui è a riposo. Un osservatore nel sistema F lo vede contratto di un fattore γ, come mostrato a destra in figura.
La diversa relazione tra t' e t ribalta le cose e determina invece una “dilatazione temporale” di quanto accade nel sistema F' visto nel sistema F, data dallo stesso fattore γ.
Ne danno una prova le particelle dette “ muoni ” generate assieme ad altre nelle interazioni di raggi cosmici negli strati alti dell’atmosfera, come mostrato in figura 8 tramite una simulazione al calcolatore. I muoni sono particelle penetranti e in linea di principio possono giungere alla superficie terrestre, impiegando un tempo t = L / c di circa 30 microsecondi (milionesimi di secondo) per percorrere i circa L = 10 km di atmosfera terrestre a una velocità prossima a quella della luce c = 300.000 km/s. Ma essi sono instabili, con tempo di vita medio di circa 2 microsecondi nel sistema in cui essi sono a riposo. Come possono farcela? Il fattore di Lorentz rallenta i loro orologi e allunga la loro vita, come vista stando sulla superficie terrestre: la loro sopravvivenza è dovuta alla dilatazione temporale.
Teoria della Relatività Speciale
Con un procedere prettamente teorico, Albert Einstein (allora ventiseienne) formulò nel 1905 la “ Teoria della Relatività Speciale ” (anche detta “Ristretta”), limitandosi a sistemi di riferimento in moto relativo rettilineo e uniforme (“inerziali”) e riprendendo l’idea di invarianza delle leggi fisiche che aveva ispirato Galileo. In poche concise parole egli ne esprime l’intuizione (“insight”, come egli stesso dice) di base:
Ragioniamo ora sull'energia E. La relazione classica E = ½ mv 2 non può più valere perché la velocità satura a quella della luce. La massa deve farsi carico di aumenti di energia, e lo fa quella relativistica. Lasciando a parte il banale fattore numerico ½ , si capisce così la sostanza della relazione einsteiniana
La figura 9 la mostra in un manoscritto originale di Einstein, in cui m sta per la massa a riposo.
In sintesi, con la Relatività einsteiniana l'Invarianza delle leggi fisiche è assicurata anche per velocità paragonabili a quella della luce. Per esempio, F = ma vale ancora per tutti ma la massa m non è più costante. Per chi si muove lentamente come per gli iper-veloci che vorrebbero correre a velocità paragonabili a quella della luce possiamo di nuovo dire:
................
Equivalenza energia-massa
Massa ed energia sono indistinguibili concettualmente, essendo collegate unicamente dal fattore di proporzionalità costante c 2 . Non sarebbe logico fare chiarezza riducendo all'unità il suo valore numerico e fare così sparire l'inutile fardello per scrivere semplicemente E = m?
E' facile. La scelta di lunghezza, massa e tempo come grandezze di riferimento per il sistema di unità di misura (C.G.S. o altro) è praticamente sensata perché queste sono le grandezze fisiche del quotidiano, ma concettualmente arbitraria. Basta promuovere la velocità a grandezza fisica di riferimento e assumere la velocità della luce come sua unità di misura. Non vi è neanche la complicazione di conservarne gelosamente un campione "ufficiale" nel recondito caveau di qualche tempio della metrologia.
Questo fa il sistema di unità di misura (detto “naturale”) usato in fisica delle particelle, alla cui scala di dimensioni metro o altro che sia usato nel quotidiano non hanno comunque interesse pratico.
Paradossi
La rottura con il passato introdotta dalla Teoria della Relatività è clamorosa. Le conseguenze sono impressionanti e con aspetti paradossali: è noto il " paradosso dei gemelli ".
Da tempi antichi, anche nel pensiero filosofico il paradosso - frutto della logica basato sull'osservazione - è indicatore di novità e stimolo a conoscenza:
Semplicità del formalismo relativistico
L'impossibilità di separare il tempo dalle coordinate spaziali impone di considerarle tutte insieme e rende ogni rappresentazione matematica a prima vista più complessa. Basta a mostrarlo un paragone la trasformazione di Lorentz a quella galileiana.
Ma non spaventatevi se un giorno dovrete affrontare dei calcoli relativistici: il potere di astrazione e semplificazione formale della matematica entra sempre in soccorso degli esseri umani desiderosi di fare Scienza, per rendere agevole il calcolo anche con l’aumentare della complessità. Anzi, in casi come questo stravince. Gli usuali “(tri-)vettori” ci salvano dal doversi sempre "tirare dietro" tutte e tre le coordinate spaziali x-y-z prese per mano una per una: basta un unico simbolo vettoriale r, con il tempo da considerare in aggiunta a parte. L'usuale formalismo relativistico condensa addirittura tutte e quattro le dimensioni x-y-z-t in un unico “quadri-vettore” e permette di procedere in modo ancora più sintetico e spedito.
Ne fornisce un esempio strepitoso la famosa Equazione di Dirac , che nel 1927 fornì la prima rappresentazione relativistica del comportamento dell’elettrone, valida anche per altre particelle elementari. la prodigiosa intuizione di Dirac nel concepirla portò a ulteriori e sorprendenti frutti.
Ebbene, osservate in figura 11 la formale semplicità dell'Equazione di Dirac e anche quella che egli stesso chiamò "bellezza matematica".
Teoria della Relatività Generale
La Teoria della Relatività Speciale fu seguita nel 1915-1916 dalla " Teoria della Relatività Generale ", non soggetta alla limitazione di moto relativo rettilineo e uniforme dei due sistemi ma sempre basata sul presupposto di invarianza delle leggi fisiche. Da essa scaturì una visione totalmente nuova dello spazio-tempo e della Gravitazione. Ne diamo solo un accenno, rinviando a Interazione Gravitazionale per maggiori precisazioni.
La Teoria della Relatività Generale dà alle masse un "ruolo attivo" nel determinare le caratteristiche dello spazio-tempo, precedentemente totalmente disaccoppiato da una loro presenza. Non solo il tempo, ma anche lo spazio-tempo non ha più vita autonoma e imperturbata. Sentiamolo dire da Einstein:
.................
Fig. 12. Un’analogia alla deformazione dello spazio-tempo indotta da una massa e alla conseguente forza attrattiva - Immagine The Physics mill
La Relatività Generale interpreta l’attrazione gravitazionale come effetto di una “deformazione dello spazio-tempo” indotta dalle masse stesse, come descritto in modo lapidario da John Archibald Wheeler :
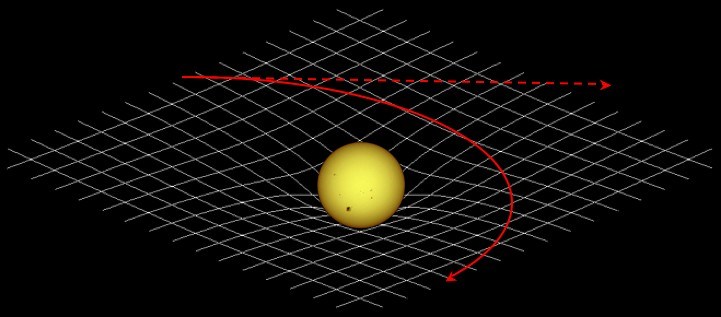
Per avere un’idea visiva dell’effetto creato dalla presenza di una massa, trasponiamolo dalle quattro dimensioni dello spazio-tempo relativistico alle tre del nostro spazio sensoriale. La figura 12 (ispirata al disegno di Wheeler associato alla suddetta citazione) mostra la deformazione di una invisibile membrana per effetto della massa di un corpo posato su di essa. La deformazione fa "cadere" un altro corpo verso di essa o ne devia la traiettoria. Non vedendo la deformazione della membrana, attribuiamo l’effetto a una forza attrattiva tra i due corpi.
Tutto è cominciato da pescetti e farfalle
La nostra prima volta con la parola "Relatività" è generalmente caratterizzata da sconcerto e timore che il suo significato sia al di là della nostra mente. Questo è anche l'effetto che essa desta nel grande pubblico.
Me le questioni fondamentali della Scienza nascono da semplicità e giungono a semplicità, unita a bellezza. La Teoria della Relatività è iniziata con i pescetti e le farfalle nel navilio di Galileo, che forniscono un'immagine accessibile a tutti al fine di mostrare quanto sia vicina a noi la questione dell'invarianza delle leggi fisiche.
Pensando alla confusione che altrimenti nascerebbe nei moti spesso frenetici della nostra vita pratica, ci rendiamo conto di quanto sia fondamentale che essa sia rispettata. Lo è anche per la farfalla in figura 1, che vola diritta verso un fiore. Nulla le importa che ambedue seguano il moto della Terra.
Per approfondire
La rivista Asimmetrie ( numero 11, 2011 ) offre letture complementari attraverso articoli dedicati a Simmetrie e Asimmetrie nei loro diversi aspetti e attualità.
Per maggiori dettagli sulla Trasformazione di Lorentz e sulla Relatività Speciale, potete vedere: Nicola Santoro, Elementi di Relatività Ristretta .
La Fisica di Feynman regala sempre il piacere di capire la sostanza e di apprezzare bellezza. In particolare, vedete La teoria della relatività speciale (Cap. 15, Vol 1), Energia e quantità di moto relativistiche (Cap. 16, Vol. 1), Spazio-tempo, (Cap. 17, Vol. 1), La simmetria nelle leggi fisiche (Cap. 52, Vol. 1) e L’invarianza delle equazioni dell’elettrodinamica (Cap. 25-6, Vol. 2).
..
.
Professore Emerito di Fisica Sperimentale
Università di Napoli "Federico II"
Complesso Univ. Monte S. Angelo
Via Cintia - 80126 Napoli - Italy
Simmetrie e Relatività Speciale è stato creato da P. Strolin
Simmetrie e Relatività Speciale
................
................
Per domande: autore o
Domanda a un esperto
................| .......................................................................................
Fig. 1. Volo di farfalla relativamente a un fiore Michele Monari - Immagine Michele Monari - Nikonclub Clic per alta definizione | ...... | ................................ Può una farfalla rispondere a una domanda fondamentale, che vale per ogni dominio della Scienza: le leggi della Natura sono le stesse in sistemi di riferimento in moto uno rispetto all’altro? Se non fossero “invarianti” si creerebbe una gran disorientamento e si porrebbero seri e sostanziali problemi. Sarebbe contento solo chi fosse in cerca di pretesti per non studiarle. La farfalla in figura 1 (vedete la fotografia ingrandita: è bellissima) ci rassicura. Le sue ali usano le leggi della dinamica in un mezzo fluido per farla muovere con sicurezza verso il fiore. Prendendo spunto dal brano di Galileo che riporteremo a breve, sfatiamo ogni timore per la parola Relatività e avviciniamoci ad essa in poche parole: ................
"Relatività è un volo di farfalla verso un fiore, senza avvertire
il moto della Terra rispetto a un sistema di riferimento celeste”. Qualunque ne sia il moto, le leggi fisiche sono sempre "relative" al sistema in cui ci troviamo. Esse trovano uguale formulazione relativamente a qualsiasi sistema, e non vanno considerate valide solo in un fantomatico sistema di riferimento assoluto. In linea di principio e senza limitarsi a voli di farfalle, la forma dell'enunciato vale sia per la Relatività galileiana che per quella einsteiniana. La più generale formulazione di quest'ultima ne estende la validità anche a casi con velocità non trascurabili rispetto a quella della luce. |
Partendo dalla Relatività galileiana, proseguiremo con la costanza della velocità della luce nelle Equazioni di Maxwell e l'esperimento di Michelson-Morley. Giungeremo infine alla Trasformazione di Lorentz e alla Teoria della Relatività nella sua formulazione più semplice, detta Speciale o Ristretta e limitata a un moto relativo uniforme.
Invarianza e simmetria
La "simmetria" di un cristallo consiste in una "invarianza" rispetto a specifiche rotazioni del cristallo stesso. In generale, vi è uno strettissimo legame tra i concetti di invarianza e di simmetria, evidenziato in Simmetrie: dai solidi platonici ai cristalli minerali . Volendo essere assolutamente precisi nel linguaggio, in Fisica si parla di "invarianza" di una grandezza fisica e di "covarianza" della formulazione di una legge fisica rispetto al sistema di riferimento. Per semplicità, concentreremo questi due concetti in uno e parleremo solo di invarianza.
La simmetria che porta alla Relatività consiste nell'invarianza delle leggi fisiche rispetto a trasformazioni di coordinate tra due sistemi in moto relativo uno rispetto all'altro.
Relatività galileiana
Galileo Galilei fu grande scienziato e grande comunicatore della Scienza, come gli era vitale al fine di convincere la Chiesa che stando sulla Terra non possiamo percepire il suo moto attorno al Sole. Nella seconda giornata del Dialogo sopra i due massimi sistemi del mondo (pubblicazione autorizzata nel 1632, vedetene il frontespizio in figura 2), Salviati - difensore della teoria copernicana - dice:
| ..........................................................................................................................................
Fig. 2. Galileo Galilei, Dialogo sopra i due massimi sistemi del mondo, Prima edizione (1632) Immagine University of Missouri - Clic per alta definizione da Perkins School of Theology | ...... | ................................ "Rinserratevi con qualche amico nella maggiore stanza che sia sotto coverta di alcun gran navilio, e quivi fate d'aver mosche, farfalle e simili animaletti volanti: siavi anco un gran vaso d'acqua, e dentrovi de' pescetti; sospendasi anco in alto qualche secchiello, che a goccia a goccia vada versando dell'acqua in un altro vaso di angusta bocca che sia posto a basso; e stando ferma la nave, osservate diligentemente come quelli animaletti volanti con pari velocità vanno verso tutte le parti della stanza. [...] Fate muovere la nave con quanta si voglia velocità; |
ché (pur di moto uniforme e non fluttuante in qua e in là) voi non riconoscerete una minima mutazione in tutti li nominati effetti; né da alcuno di quelli potrete comprendere se la nave cammina, o pure sta ferma".
Il discorso vale anche per l’astronauta di oggi nel suo astro-navilio, pur se non ha pescetti o farfalle. Notate come Galileo esprime la “Invarianza” delle leggi della Meccanica: per sistemi in moto lineare e uniforme ("non fluttuante") uno rispetto all'altro:
................
"... voi non riconoscerete una minima mutazione in tutti li nominati effetti ..."
La “Relatività Galileiana" è figlia dell'Invarianza osservata nel navilio ed è collegata alla ben nota ta “trasformazione galileiana” delle coordinate spaziali x-y-z, con il tempo t che scorre autonomamente oltre che in modo inarrestabile. Essa implica un'addizione algebrica delle velocità: dati due sistemi di riferimento F' e F, la velocità V' di un corpo in F' è data dalla velocità V in F meno la velocità v di F' relativamente F, cioè per un moto lungo l'asse x:
................
x' = x - vt ........................... V' = V - v.
La trasformazione galileiana assicura l'Invarianza delle leggi fisiche a lui note, e in particolare F = ma.
................
"La legge fisica è uguale per tutti".
La luce non si cura del sistema di riferimento
Nel 1864 James Clerk Maxwell unificò fenomeni elettrici e magnetici formulando le leggi dell'elettro-magnetismo mediante le sue famose equazioni, come è delineato nell'articolo Interazioni elettro-magnetiche "alla Fenyman" . Esse dicono che nel vuoto le onde elettro-magnetiche, la luce in primis, si propagano tutte e sempre con la stessa velocità c e hanno quindi l'Invarianza "costruita dentro".
Secondo Maxwell, la luce non si cura della relatività galileiana, che prevede l'addizione di velocità. Anzi la relatività galileiana porterebbe a problemi: definita la velocità della luce in un sistema di riferimento, essa potrebbe esserne superiore in un'altro. Fu grande mistero, e grande finestra aperta sul futuro.
Nel 1887 l'esperimento di Michelson-Morley, del quale ci accingiamo a parlare, mostrò sperimentalmente che effettivamente la luce non si cura della velocità con cui ci muoviamo nello spazio assieme alla Terra. Non vi è bisogno di immaginare un ipotetico " etere " per cui valgano le Equazioni di Maxwell. La loro Invarianza, e assieme a essa quella della velocità della luce, fu anche realtà sperimentale da rispettare:
................
"La velocità della luce è uguale per tutti".
| ..................... ..... Fig. 3a. L'apparato sperimentale di Michelson-Morley Dall’articolo originale del 1887 - Immagine Wikipedia | ..... | ................................
Fig. 3b. Schema dell'ottica dell'interferometro Michelson-Morley Dall’articolo originale del 1887 - Immagine Wikipedia |
Esperimento di Michelson-Morley
I fenomeni di interferenza – caratteristici della natura ondulatoria - possono essere efficacemente utilizzati misurare con precisione la velocità della luce, come onda elettromagnetica.
Albert Michelson iniziò nel 1881 le sue famose misure sulla velocità della luce, completate nel 1887 mediante l’ interferometro da lui costruito assieme a Edward Morley. Come si è detto, nel 1864 dalle Equazioni di Maxwell la velocità della luce era sorprendentemente emersa come una costante. Le Equazioni di Maxwell dovevano considerarsi valide nel sistema di riferimento di un ipotetico “etere”? Se così fosse, l’addizione galileiana delle velocità della luce e della Terra rispetto all’etere avrebbe dovuto manifestarsi in velocità diverse secondo due direzioni ortogonali. Michelson confutò questa ipotesi, confrontando la velocità della luce nei due bracci ortogonali di un “interferometro”. Egli mostrò che la velocità della luce è la stessa nei due bracci, con un errore abbastanza piccolo da escludere un'addizione galileiana di velocità. Michelson ebbe il Premio Nobel 1907 .
Le figure 3a e 3b, tratte dalla pubblicazione originale mostrano l’apparato sperimentale e lo schema dell’ottica. Una stessa sorgente (a) invia luce bianca in due bracci ortogonali lunghi poco più di un metro, tra i quali è suddivisa tramite uno specchio semi-riflettente (b). Una lastrina di vetro è inserita nel braccio ove la luce non attraversa lo specchio, per equalizzare la lunghezza dei percorsi della luce nei due bracci. La luce è quindi riflessa (d, e) e ricombinata prima di giungere al rivelatore (f), ove è osservata l'interferenza tra la luce in un braccio e quella nell'altro. La lunghezza efficace di ciascun braccio è estesa a 11 m tramite 8 riflessioni, al fine di amplificare il percorso della luce e la sensibilità della misura.
| .....................
Fig. 4. Formazione delle frange d’interferenza secondo Michelson e Morley Dall’articolo originale del 1887 - Immagine Wikisource | ..... | ................................ ..... Fig. 5. Frange d’interferenza con luce bianca come nell'esperimento di Michelson-Morley - Immagine Wikipedia |
La figura 4 mostra l’interferometro nel sistema di riferimento dell’ipotetico etere, nel caso di moto di traslazione orizzontale dell’interferometro rispetto ad esso. Alla fine del suo viaggio di ritorno, la luce nel braccio verticale avrebbe trovato lo specchio spostato e, quindi, la necessità di percorrere una distanza maggiore, come schematicamente mostrato.
La figura 5 mostra le frange di interferenza in un interferometro come quello di Michelson-Morley. Notate il deterioramento della misura introdotto dall’effetto di dispersione cromatica , legato all’uso della luce "bianca" emessa dal Sole, con tutte le sue componenti spettrali .
L’interferometro poteva essere ruotato, al fine di paragonare la velocità della luce in direzioni ortogonali. Esso era montato su un blocco di pietra con 1,5 m di lato e isolato al meglio dalle vibrazioni, altrimenti:
“it was impossible to see the interference fringes except at brief intervals when working in the city, even at two o'clock in the morning”
(lavorando in città era impossibile vedere le frange di interferenza tranne che a brevi intervalli, anche alle due del mattino).
Gli autori stimavano di avere un limite di sensibilità pari a 1/100 della larghezza delle frange. Non fu osservato alcun effetto compatibile con una diversa velocità della luce nei due bracci per addizione galileiana di velocità.
Notate che l'interferometro di Michelson e Morley ha dato concettualmente origine agli attuali "Interferometri Laser" per l'osservazione di "Onde gravitazionali" (vedete Onde gravitazionali dall'oceano cosmico e Onde gravitazionali e laser: Einstein & Einstein )
Trasformazione di Lorentz
Dall'esigenza - teorica con le Equazioni di Maxwell e sperimentale con l'esperimento di Michelson e Morley - di rispettare l'Invarianza della velocità della luce scaturì nell’ultimo decennio dell’Ottocento la " trasformazione di Lorentz ". La denominazione fu data da Poincaré, che nel 1905 la pose nella forma attuale.
Come quella galileiana, la trasformazione di Lorentz si applica a sistemi in moto rettilineo e uniforme uno relativamente all’altro. Essa è mostrata schematicamente in figura 6, per un sistema F’ che si muove con velocità costante v lungo l’asse x rispetto al sistema F.
................................
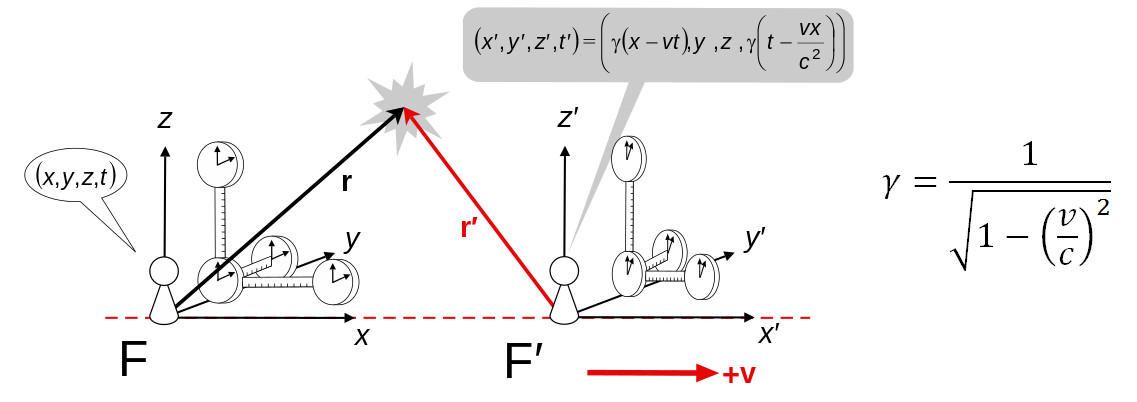
Fig. 6. Trasformazione di Lorentz e contemporaneità. A destra il fattore di Lorentz γ - Immagine a sinistra Wikipedia
Fig. 6. Trasformazione di Lorentz e contemporaneità. A destra il fattore di Lorentz γ - Immagine a sinistra Wikipedia
Iniziamo con una riflessione sul concetto di "contemporaneità" per segnali provenienti da sistemi in moto relativo. Per una velocità infinita di propagazione dei segnali, si può anche impunemente pensarla come riferita agli istanti di emissione. La velocità finita della luce c fornisce il limite di quella di propagazione dei segnali e impone un totale rigore logico: la contemporaneità non può che essere riferita al sistema e agli istanti in cui i segnali vengono osservati, come schematizzato dalla stella in figura.
Ne consegue che il tempo non è più un’entità assoluta e indipendente dallo spazio come per Galileo, ma dipende dal moto del sistema a cui si riferisce. I fenomeni devono essere visti in uno “spazio-tempo” e non più nello spazio "e" nel tempo. Entriamo in un nuovo mondo a quattro dimensioni (4D, secondo il dire usuale), con le tre dimensioni spaziali inseparabili da quella temporale: una rivoluzione del pensiero scientifico e filosofico.
Le coordinate spazio-temporali (x’, y', z’, t’) nel sistema F’ sono legate a quelle (x, y, z, t) nel sistema F dalla relazione indicata nell’inserto a fumetto in figura 6. Il fondamentale "fattore di Lorentz" γ è dato a destra in figura ed è funzione del rapporto v/c.
La pura addizione galileiana delle velocità è sostituita dalla relazione:
................
ove V e V’ sono le velocità nei due sistemi di riferimento. Per V = c si ha anche V' = c : la velocità v del sistema F’ rispetto a F non aggiunge o toglie nulla e l’invarianza della velocità della luce c è rispettata.
Per velocità v trascurabili rispetto a quella della luce c, il fattore di Lorentz γ vale 1 e si ritrova la trasformazione galileiana
................
x' = x - vt ........................... V' = V - v.
con il tempo identico nei due sistemi. La trasformazione di Lorentz ha carattere più generale di quella galileiana, che resta un’approssimazione valida nel suo dominio. La Scienza avanza innovando senza smentirsi.
| .................................................................................
Fig. 7. Hendrik Lorentz - Immagine Wikimedia Commons A destra: la “contrazione di Lorentz” presa letteralmente | ..... | ..... | ...........................
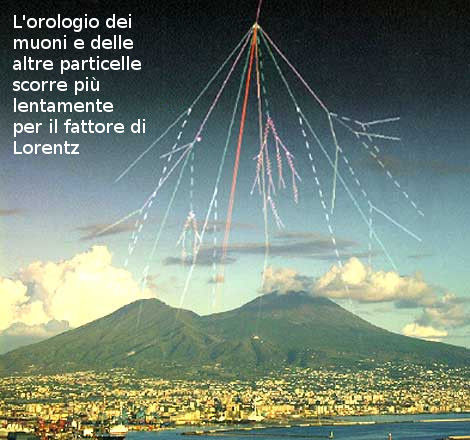
Fig. 8. Uno sciame di particelle, tra le quali muoni, generate nell’interazione di raggi cosmici nell’atmosfera (simulazione al calcolatore) Immagine MU-RAY – Provincia di Napoli |
Contrazione spaziale e dilatazione temporale
Il fattore di Lorentz, che aumenta al crescere del rapporto v/c, porta una contrazione delle lunghezze nel sistema F' viste in F. E' la cosiddetta “contrazione di Lorentz”, mostrata schematicamente in figura 6. Ma è più divertente prendere alla lettera la sua denominazione, secondo un'idea tratta da Spacetime . La figura 7 a sinistra mostra Hendrik Lorentz (1853-1928) nel sistema di riferimento F’ in cui è a riposo. Un osservatore nel sistema F lo vede contratto di un fattore γ, come mostrato a destra in figura.
La diversa relazione tra t' e t ribalta le cose e determina invece una “dilatazione temporale” di quanto accade nel sistema F' visto nel sistema F, data dallo stesso fattore γ.
Ne danno una prova le particelle dette “ muoni ” generate assieme ad altre nelle interazioni di raggi cosmici negli strati alti dell’atmosfera, come mostrato in figura 8 tramite una simulazione al calcolatore. I muoni sono particelle penetranti e in linea di principio possono giungere alla superficie terrestre, impiegando un tempo t = L / c di circa 30 microsecondi (milionesimi di secondo) per percorrere i circa L = 10 km di atmosfera terrestre a una velocità prossima a quella della luce c = 300.000 km/s. Ma essi sono instabili, con tempo di vita medio di circa 2 microsecondi nel sistema in cui essi sono a riposo. Come possono farcela? Il fattore di Lorentz rallenta i loro orologi e allunga la loro vita, come vista stando sulla superficie terrestre: la loro sopravvivenza è dovuta alla dilatazione temporale.
Teoria della Relatività Speciale
Con un procedere prettamente teorico, Albert Einstein (allora ventiseienne) formulò nel 1905 la “ Teoria della Relatività Speciale ” (anche detta “Ristretta”), limitandosi a sistemi di riferimento in moto relativo rettilineo e uniforme (“inerziali”) e riprendendo l’idea di invarianza delle leggi fisiche che aveva ispirato Galileo. In poche concise parole egli ne esprime l’intuizione (“insight”, come egli stesso dice) di base:
“The universal principle of the special theory of relativity is contained in the postulate: The laws of physics are invariant with respect to Lorentz transformations (for the transition from one inertial system to any other arbitrarily chosen inertial system)”.
Il principio universale della teoria della relatività è contenuto nel postulato: le leggi della fisica sono invarianti rispetto alle trasformazioni di Lorentz (per il passaggio da un sistema inerziale a qualsiasi altro sistema inerziale scelto arbitrariamente).
(A. Einstein, Autobiographical Notes, 1949)
Il principio universale della teoria della relatività è contenuto nel postulato: le leggi della fisica sono invarianti rispetto alle trasformazioni di Lorentz (per il passaggio da un sistema inerziale a qualsiasi altro sistema inerziale scelto arbitrariamente).
(A. Einstein, Autobiographical Notes, 1949)
| ....................................................................................
Fig. 9. Energia, massa a riposo e massa relativistica in un manoscritto di Albert Einstein Immagine Daily KOS –University of Leiden – Einstein Archive | ..... | ........................... Le acque iniziano a muoversi attorno al concetto di massa. La velocità della luce rappresenta un limite invalicabile. Se vogliamo che la legge della dinamica F = ma resti valida e che la velocità non possa crescere all'infinito, la massa e l'inerzia che essa rappresenta devono rinunciare all'idea di rimanere costanti e tendere all'infinito per velocità che approssimano quella della luce. La massa classicamente considerata nelle leggi della dinamica va accettata solo per velocità trascurabili rispetto a quella della luce e al limite nulle, cioè come “massa a riposo” m o . Il fattore di Lorentz γ sembrerà anche a voi fatto apposta come fattore di proporzionalità per far tendere all'infinito la massa m con la velocità. Si capisce così la sostanza della relazione relativistica
m = γ m
o
|
Ragioniamo ora sull'energia E. La relazione classica E = ½ mv 2 non può più valere perché la velocità satura a quella della luce. La massa deve farsi carico di aumenti di energia, e lo fa quella relativistica. Lasciando a parte il banale fattore numerico ½ , si capisce così la sostanza della relazione einsteiniana
E = mc
2
.
La figura 9 la mostra in un manoscritto originale di Einstein, in cui m sta per la massa a riposo.
In sintesi, con la Relatività einsteiniana l'Invarianza delle leggi fisiche è assicurata anche per velocità paragonabili a quella della luce. Per esempio, F = ma vale ancora per tutti ma la massa m non è più costante. Per chi si muove lentamente come per gli iper-veloci che vorrebbero correre a velocità paragonabili a quella della luce possiamo di nuovo dire:
................
"La legge fisica è uguale per tutti".
Equivalenza energia-massa
Massa ed energia sono indistinguibili concettualmente, essendo collegate unicamente dal fattore di proporzionalità costante c 2 . Non sarebbe logico fare chiarezza riducendo all'unità il suo valore numerico e fare così sparire l'inutile fardello per scrivere semplicemente E = m?
E' facile. La scelta di lunghezza, massa e tempo come grandezze di riferimento per il sistema di unità di misura (C.G.S. o altro) è praticamente sensata perché queste sono le grandezze fisiche del quotidiano, ma concettualmente arbitraria. Basta promuovere la velocità a grandezza fisica di riferimento e assumere la velocità della luce come sua unità di misura. Non vi è neanche la complicazione di conservarne gelosamente un campione "ufficiale" nel recondito caveau di qualche tempio della metrologia.
Questo fa il sistema di unità di misura (detto “naturale”) usato in fisica delle particelle, alla cui scala di dimensioni metro o altro che sia usato nel quotidiano non hanno comunque interesse pratico.
Paradossi
La rottura con il passato introdotta dalla Teoria della Relatività è clamorosa. Le conseguenze sono impressionanti e con aspetti paradossali: è noto il " paradosso dei gemelli ".
Da tempi antichi, anche nel pensiero filosofico il paradosso - frutto della logica basato sull'osservazione - è indicatore di novità e stimolo a conoscenza:
| ....................................................................................
Fig. 10. La conseguenza logica come strumento di ironia - Immagine Fumettolosteriaulisse | ..... | ....................... “Quanto più paradossale e straordinario è l'enigma, tanto più pare ammonirci a non affidarci alla nuda parola, ma ad affaticarci intorno alla verità riposta”. Giuliano l’Apostata (331-363), Imperatore Romano, Contra Heraclium cynicum 217 c E in tempi relativamente recenti: “Togli il paradosso da un pensatore e avrai un professore”. Søren Kierkegaard (1813-1855), Diario Si può benevolmente supporre che egli abbia inteso un professore che insegni nozioni congelate, piuttosto che trasmettere idee vive. Ma il discorso spinto oltre il previsto e verso il limite è anche presente nella nostra vita di tutti i giorni, nell'ironia e nella satira. Vedete ad esempio la vignetta in figura 10. |
Semplicità del formalismo relativistico
L'impossibilità di separare il tempo dalle coordinate spaziali impone di considerarle tutte insieme e rende ogni rappresentazione matematica a prima vista più complessa. Basta a mostrarlo un paragone la trasformazione di Lorentz a quella galileiana.
Ma non spaventatevi se un giorno dovrete affrontare dei calcoli relativistici: il potere di astrazione e semplificazione formale della matematica entra sempre in soccorso degli esseri umani desiderosi di fare Scienza, per rendere agevole il calcolo anche con l’aumentare della complessità. Anzi, in casi come questo stravince. Gli usuali “(tri-)vettori” ci salvano dal doversi sempre "tirare dietro" tutte e tre le coordinate spaziali x-y-z prese per mano una per una: basta un unico simbolo vettoriale r, con il tempo da considerare in aggiunta a parte. L'usuale formalismo relativistico condensa addirittura tutte e quattro le dimensioni x-y-z-t in un unico “quadri-vettore” e permette di procedere in modo ancora più sintetico e spedito.
Ne fornisce un esempio strepitoso la famosa Equazione di Dirac , che nel 1927 fornì la prima rappresentazione relativistica del comportamento dell’elettrone, valida anche per altre particelle elementari. la prodigiosa intuizione di Dirac nel concepirla portò a ulteriori e sorprendenti frutti.
| ...........................................................................
Fig. 11. L’equazione di Dirac Immagine +Magazine, Dirac Centennial | ..... | ...................... La prima sorpresa fu l’automatica e inattesa inclusione nell’equazione stessa di una tuttora inspiegabile ma reale proprietà dell’elettrone: il suo “momento angolare di spin”, con le relative variabili per rappresentarlo (vedete Lo spin e altri sull'argomento tra i Saggi tematici ). L’Equazione di Dirac fornì inoltre la rivoluzionaria predizione dell’esistenza di anti-particelle . La predizione di Dirac trovò conferma nel 1932 con la scoperta dell’anti-elettrone, comunemente detto “ positrone ”. |
Ebbene, osservate in figura 11 la formale semplicità dell'Equazione di Dirac e anche quella che egli stesso chiamò "bellezza matematica".
Teoria della Relatività Generale
La Teoria della Relatività Speciale fu seguita nel 1915-1916 dalla " Teoria della Relatività Generale ", non soggetta alla limitazione di moto relativo rettilineo e uniforme dei due sistemi ma sempre basata sul presupposto di invarianza delle leggi fisiche. Da essa scaturì una visione totalmente nuova dello spazio-tempo e della Gravitazione. Ne diamo solo un accenno, rinviando a Interazione Gravitazionale per maggiori precisazioni.
La Teoria della Relatività Generale dà alle masse un "ruolo attivo" nel determinare le caratteristiche dello spazio-tempo, precedentemente totalmente disaccoppiato da una loro presenza. Non solo il tempo, ma anche lo spazio-tempo non ha più vita autonoma e imperturbata. Sentiamolo dire da Einstein:
"According to General Relativity, the concept of space(-time)
detached from any physical content (la presenza di masse) does not exist".
Secondo la Relatività Generale, il concetto di spazio(-tempo)
distaccato da ogni contenuto fisico (la presenza di masse) non esiste
A. Einstein, On the generalized theory of gravitation, Scientific American, Aprile 1950
.detached from any physical content (la presenza di masse) does not exist".
Secondo la Relatività Generale, il concetto di spazio(-tempo)
distaccato da ogni contenuto fisico (la presenza di masse) non esiste
A. Einstein, On the generalized theory of gravitation, Scientific American, Aprile 1950
.................
Fig. 12. Un’analogia alla deformazione dello spazio-tempo indotta da una massa e alla conseguente forza attrattiva - Immagine The Physics mill
La Relatività Generale interpreta l’attrazione gravitazionale come effetto di una “deformazione dello spazio-tempo” indotta dalle masse stesse, come descritto in modo lapidario da John Archibald Wheeler :
"Matter tells spacetime how to curve, and curved spacetime tells matter how to move".
La materia dice allo spazio-tempo come curvarsi e lo spazio-tempo curvo dice alla materia come muoversi.
J.A. Wheeler, Geons, Black Holes, and Quantum Foam, pag. 235
La materia dice allo spazio-tempo come curvarsi e lo spazio-tempo curvo dice alla materia come muoversi.
J.A. Wheeler, Geons, Black Holes, and Quantum Foam, pag. 235
Per avere un’idea visiva dell’effetto creato dalla presenza di una massa, trasponiamolo dalle quattro dimensioni dello spazio-tempo relativistico alle tre del nostro spazio sensoriale. La figura 12 (ispirata al disegno di Wheeler associato alla suddetta citazione) mostra la deformazione di una invisibile membrana per effetto della massa di un corpo posato su di essa. La deformazione fa "cadere" un altro corpo verso di essa o ne devia la traiettoria. Non vedendo la deformazione della membrana, attribuiamo l’effetto a una forza attrattiva tra i due corpi.
| .........................................................................................
Fig. 13. Effetto della dilatazione temporale sui tempi misurati sui satelliti GPS rispetto a quelli dati dagli orologi a terra Immagine di sfondo Wikiwand | ..... | ........................... La Teoria della Relatività e noi Anche se non ne siamo sempre coscienti, la Teoria della Relatività fa parte della nostra vita di tutti i giorni. Ad esempio il “ Sistema di Posizionamento Globale ” (in inglese “Global Positioning System” da cui l’acronimo GPS), utilizzato anche dai nostri telefonini per dirci dove siamo e dirigerci dove desideriamo, deve tener conto degli effetti relativistici di dilatazione temporale. Come indicato in figura 13, per effetti della Teoria della Relatività (Speciale e Generale) gli orologi situati sui satelliti del Sistema GPS avanzano in totale di 38 microsecondi (milionesimi di secondo) al giorno rispetto a quelli a terra. Ove non se ne tenesse conto, questo anticipo moltiplicato per la velocità della luce porterebbe a un errore di posizione di circa 10 km, tale da rendere inutile ogni dispositivo. Vedete per esempio il seminario Il Sistema di Posizionamento Globale . |
Tutto è cominciato da pescetti e farfalle
La nostra prima volta con la parola "Relatività" è generalmente caratterizzata da sconcerto e timore che il suo significato sia al di là della nostra mente. Questo è anche l'effetto che essa desta nel grande pubblico.
Me le questioni fondamentali della Scienza nascono da semplicità e giungono a semplicità, unita a bellezza. La Teoria della Relatività è iniziata con i pescetti e le farfalle nel navilio di Galileo, che forniscono un'immagine accessibile a tutti al fine di mostrare quanto sia vicina a noi la questione dell'invarianza delle leggi fisiche.
Pensando alla confusione che altrimenti nascerebbe nei moti spesso frenetici della nostra vita pratica, ci rendiamo conto di quanto sia fondamentale che essa sia rispettata. Lo è anche per la farfalla in figura 1, che vola diritta verso un fiore. Nulla le importa che ambedue seguano il moto della Terra.
| ...............................................................................................................
Fig. 14. La farfalla si è posata Michele Monari - Immagine Michele Monari - Nikonclub Clic per alta definizione | ...... | ................................ La Scienza non fa che osservare i fenomeni e sintetizzarne i messaggi in costruzioni teoriche che danno risposte a questioni allo stesso tempo semplici e fondamentali, e ne proiettano le conseguenze verso un mondo che potrebbe a volte sembrare far parte della pura immaginazione o almeno della fantascienza. La Relatività einsteiniana è scaturita dall'osservazione di fenomeni totalmente nuovi, ma come per quella galileiana la sua origine profonda sta in pescetti e le farfalle. Insieme ai pescetti, le farfalle hanno avuto il loro ruolo nella Scienza e possono anche posarsi e riposare. Come quella mostrata in figura 14. |
Per approfondire
La rivista Asimmetrie ( numero 11, 2011 ) offre letture complementari attraverso articoli dedicati a Simmetrie e Asimmetrie nei loro diversi aspetti e attualità.
Per maggiori dettagli sulla Trasformazione di Lorentz e sulla Relatività Speciale, potete vedere: Nicola Santoro, Elementi di Relatività Ristretta .
La Fisica di Feynman regala sempre il piacere di capire la sostanza e di apprezzare bellezza. In particolare, vedete La teoria della relatività speciale (Cap. 15, Vol 1), Energia e quantità di moto relativistiche (Cap. 16, Vol. 1), Spazio-tempo, (Cap. 17, Vol. 1), La simmetria nelle leggi fisiche (Cap. 52, Vol. 1) e L’invarianza delle equazioni dell’elettrodinamica (Cap. 25-6, Vol. 2).
Paolo Strolin
..
.
Professore Emerito di Fisica Sperimentale
Università di Napoli "Federico II"
Complesso Univ. Monte S. Angelo
Via Cintia - 80126 Napoli - Italy
Ultima Modifica 9 Anni 2 Settimane fa da Paolo.
Si prega Accesso a partecipare alla conversazione.
Tempo creazione pagina: 0.658 secondi