Da Alan Turing al calcolo quantistico
- A. Tagliacozzo
-
Autore della discussione
- Offline
- Nuovo Utente
-

Less
Di più
10 Anni 9 Mesi fa - 5 Anni 1 Mese fa #164
da A. Tagliacozzo
Il moderno concetto di calcolatore, come macchina universale con un "hardware" programmabile in modo flessibile secondo le esigenze specifiche mediante un "algoritmo" implementato in un "software" (per usare termini moderni), fu introdotto dal grande matematico inglese Alan Turing nel 1936, all'età di soli 24 anni. Il suo modello paradigmatico teorico, detto " Macchina di Turing " si trova descritto in varie opere e in particolare nel libro divulgativo di Roger Penrose La mente nuova dell'imperatore , del 1989. Per quanto riguarda la storia precedente, è importante ricordare la " Macchina analitica " dello scienziato inglese Charles Babbage (1791-1871), un progetto di macchina meccanica di uso generico capace di elaborare dati immessi dall'esterno mediante schede perforate secondo un programma inserito nello stesso modo.
Fig. 1. Un convoglio di navi attaccato da un U-boot tedesco nell’attraversamento dell’Atlantico durante la Seconda Guerra Mondiale
Immagine Inilossum
Nel dicembre del 1941, in seguito al proditorio attacco giapponese a Pearl Harbour , gli Stati Uniti entrarono in guerra contro il Giappone. Questo evento fu seguito pochi giorni dopo dalla dichiarazione di guerra della Germania e dell'Italia agli Stati Uniti. Imponenti convogli di navi iniziarono ad attraversare l’Atlantico per portare soccorso all’Europa in lotta. I sottomarini tedeschi (i famigerati U-Boot ) facevano strage di navi e persone. La figura 1 mostra la drammatica immagine dell'attacco di un sommergibile tedesco a un convoglio di navi nell’attraversamento dell’Atlantico nel corso della Seconda Guerra Mondiale.
Per conoscere preventivamente ove essi fossero dislocati e pronti all'attacco e quindi potersi difendere, era essenziale entrare nel sistema di comunicazioni tedesco, che erano intercettate ma incomprensibili perché criptate in codice segreto mediante con la macchina crittografica elettromeccanica Enigma .
Alan Turing si impegnò fortemente nell'ambiziosa impresa di decriptare i codici generati da Enigma e vi riuscì, come narrato nel film The Imitation Game , uscito nel 2014. In esso si intrecciano la storia della decriptazione di Enigma e quella personale di Alan Touring, con la sua genialità e la sua problematicità.
La necessità di decriptare rapidamente i codici delle comunicazioni tedesche diede impulso allo sviluppo del calcolo elettronico. Nel 1944 fu così costruito “ Colossus ”, antesignano dei calcolatori elettronici di oggi. Colossus era una macchina elettronica basata sull'uso di “ valvole termoioniche ” in sostituzione dei “ relais ” (italianizzati in “relè”) elettromeccanici. Colossus era concettualmente basato sulla Macchina di Turing e utilizzava metodologie matematiche da lui introdotte.
Le storie della decriptazione di Enigma e di Colossus rimasero nell'ombra per decenni per motivi di segreto militare legati alla "guerra fredda" tra Occidente e blocco sovietico.
Nel 1950, con un articolo dal titolo Macchine calcolatrici e intelligenza, lo stesso Alan Turing fu anche l’iniziatore della riflessione sulla "intelligenza artificiale" rispondendo a un interrogativo, che in parole correnti può essere formulato come "potranno un giorno le macchine pensare?". Con lo spettacolare sviluppo dei robot, questa interrogativo è di grande attualità.
Le figure 2 e 3 mostrano Colossus e il "circuito integrato" del calcolatore quantistico dei nostri tempi D-Wave One. Le due macchine sono separate nel tempo da una settantina d'anni di impressionante progresso scientifico e tecnologico, del quale daremo una sintesi panoramica.
Le valvole termoioniche (contenute in tubi a vuoto) furono rese obsolete dall'avvento dei dispositivi a stato solido con il " transistor ". Nel 1947, ai Laboratori Bell (New Jersey, USA) fu prodotto il primo “transistor” a materiale semiconduttore (Germanio, rimpiazzato poi da Silicio e composti). Fu la nascita di un “bistabile” elettronico. Le due possibili configurazioni (denotabili con 0 e 1) permettono di codificare numeri su base "binaria" (invece che decimale). Le operazioni algebriche vengono effettuate secondo la cosiddetta “ algebra di Boole ”, la quale agisce su variabili logiche binarie ("vero" o "falso"). Il numero di bistabili determina quanti “bit” (unità d’informazione, che può valere 0 o 1) possono essere scritti ed elaborati tramite algoritmi che si materializzano in linee di trasmissione elettrica che li connettono. Due bistabili consentono di codificare i quattro numeri da zero a tre: 00,01,10,11.
Questo modo di contare a "base 2" è semplice ed essenziale, oltre che ben prestarsi al calcolo numero. Siamo abituati al conteggio a "base 10", ma la scelta è arbitraria e viene da tempi in cui non si conoscevano le motivazione teoriche e i vantaggi pratici del calcolo a base 2. Se per la vita di tutti i giorni dovessimo ora scegliere una base prossima a 10, sceglieremmo piuttosto una base multipla di due come lo è 8.
L'epopea italiana
Con la Olivetti l’Italia iniziò all’avanguardia. Nel 1959 l'ingegnere italo-cinese Mario Tchou , talento eccezionale scoperto da Adriano Olivetti , ideò la macchina “ Elea 9003 ” (la terza della serie, figura 4) disegnata nelle forme dall’architetto Ettore Sottsass . Fu il primo elaboratore “ mainframe ” (cioè a sistema centrale, generalmente di grandi dimensioni), tutto a transistor. ELEA significa “Elaboratore ELettronico Aritmetico” (o “Automatico”), ma rimanda alla scuola filosofica Eleatica secondo la quale anche l’uomo ha accesso alla verità e non solo gli Dei. E' divertente e interessante notare che recentemente il paradosso di Zenone di Elea su Achille e la tartaruga è in auge nello studio interpretativo, mai completo, della Fisica Quantistica. Inoltre, la Programma 101 (figura 5) della Olivetti fu il primo calcolatore da tavolo programmabile del mondo, posto in commercio nel 1965. Per riferimento ricordiamo che Apple I uscì nel 1976, approfittando dell'era della "microelettronica" (vedete a breve) e con importanti innovazioni comprendenti in primo luogo l'aggiunta di un visore,
Nel 1960 muore improvvisamente Adriano Olivetti , all'età di 59 anni. L'anno dopo, in un incidente stradale mentre si spostava da un laboratorio a un altro, muore a solo 37 anni Mario Tchou col suo autista, scontrandosi contro un camion in circostanze mai chiarite. Finisce così l'avventura italiana nei calcolatori elettronici. Essa è narrata dalla RAI-TV nelle due puntate di “ La forza di un sogno ” insieme ad altri aspetti dell’epopea di Adriano Olivetti, che ha spaziato dal campo tecnico e industriale a quello sociale e a quello culturale. Nel 1964 l’Olivetti deve cedere la Divisione Elettronica , che passa alla General Electric per poi essenzialmente scomparire. Con il dissolversi della struttura e delle sinergie formatesi al suo interno, un inestimabile capitale d'ingegno intellettuale viene disperso anche a beneficio della californiana "Silicon Valley" come presto vedremo. Resta la Società Generale Semiconduttori fondata in quei tempi, l'attuale STMicroelectronics.
D’altro canto, nel 1962 muore in circostanze perlomeno estremamente sospette e all'età di 56 anni un altro grande protagonista dell'avanzata italiana in un settore strategico: Enrico Mattei , che con l'ENI aveva osato sfidare le grandi potenze mondiali in campo petrolifero. Furono duri colpi per la crescita tecnologica e industriale dell'Italia in aspetti strategici negli anni del cosiddetto " miracolo economico italiano " avvenuto nel dopoguerra.
A testimoniare lo stato di eccellenza raggiunto dall'Italia in quei tempi, va anche ricordato Eduardo Caianiello , uno dei pionieri delle " reti neurali " per l'apprendimento e il riconoscimento mediante intelligenza artificiale. Rientrato nel 1956 in Italia dall'Università di Princeton, fondatore e direttore dell'Istituto di Fisica Teorica e Nucleare dell'Università di Napoli in un periodo di grande fervore intellettuale, nel 1968 egli fonda l'Istituto di Cibernetica del CNR ad Arco Felice presso Pozzuoli, che vari decenni dopo sarà trasferito presso la fabbrica Olivetti di Pozzuoli ormai non più produttiva.
Questa è storia passata, seppellita dallo sviluppo tumultuoso e irrefrenabile degli ultimi 40 anni.
Entra in gioco la microelettronica
Verso la fine degli anni ’50 sono prodotti i primi “ circuiti integrati ”. In essi i vari componenti, tra i quali i transistors, sono formati tutti assieme su una sola placchetta tramite un unico processo fisico-chimico. Il dispositivo elettronico a stato solido nel suo complesso è comunemente detto “chip”, in italiano “fettina”. Nasce così la “microelettronica”. Essa è basata sulle “microtecnologie” e i suoi dispositivi hanno dimensioni misurate in micron (μm un milionesimo di metro).
I nostri attuali calcolatori utilizzano “microprocessori”. Il primo a essere commercializzato fu l’ Intel 4004 , nel 1971. Come i successivi microprocessori Intel esso fu realizzato da Federico Faggin , cresciuto nella fucina intellettuale Olivetti (di cui sopra) e poi pioniere della californiana “Silicon Valley". La figura 6 mostra gli strati superiori interconnessi del circuito integrato del microprocessore Intel 80486. La figura 7 mostra l’ Intel 8742 , che include un insieme di diversi componenti.
Con la microelettronica siamo scesi a una scala dimensionale di 30 nanometri (miliardesimi di metro), dove un atomo di Silicio ha un diametro di circa 0.2 nanometri. Nel 2020 i transistor avranno solo pochi atomi. Allo sviluppo dei microdispositivi a stato solido consegue un'impressionante riduzione delle dimensioni.
Con le dimensioni diminuiscono anche i tempi di cambiamento di stato e di trasmissione dei segnali, e cresce la velocità di operazione. La velocità massima del Pentium 4 (anno 2000) era di 1066 mega-data-transfers (milioni di trasferimenti di dati) per secondo e oggi si può arrivare ad almeno a 10.000 volte di più.
Il numero di transistors su un circuito integrato supera ormai il miliardo e si raddoppia all’incirca ogni due anni seguendo la cosiddetta “ legge di Moore ”, di carattere puramente empirico. Al crescere del numero di transistors sul circuito integrato, il costo unitario decresce ma cresce anche la possibilità che esso sia difettato e non funzioni.
D'altra parte, la capacità dei dischi rigidi che servono per immagazzinare le informazioni cresce nel tempo con una velocità circa pari a quella con cui cresce il numero di transistors.
Verso il calcolo quantistico
Con le tecniche attuali, la velocità è limitata dal consumo di energia e dal riscaldamento (le ventole dei nostri calcolatori portatili ormai affannano). Inoltre il collegare tra loro i chip e le memorie implica un tempo di propagazione del segnale: anche la velocità della luce sta diventando “lenta” per noi. Una straordinaria innovazione tecnologica è però alle porte, essendo ora all'inizio di nuova avventura: quella del “calcolo quantistico”. La fisica quantistica si è sviluppata lungo tutto il secolo scorso e siamo ormai giunti alla fabbricazione e al controllo di dispositivi quantistici di crescente raffinatezza. Le tre caratteristiche del nuovo mondo dei calcolatori quantistici saranno i nuovi materiali, la necessità di super-raffreddarli e le ridottissime dimensioni.
“Quantizzare” vuol dire ammettere grandezze che variano solo a salti e non in modo continuo. In particolare, in base al cosiddetto “ Effetto Hall quantistico ” si costruiscono dispositivi la cui “conduttanza” (l’inverso di una resistenza, e normalmente misurata in Ohm -1) procede per micro-salti di e 2/ h, ove e è carica dell'elettrone e h la “ costante di Planck ” che regge la fisica quantistica. Si noti questi dispositivi possono usare nanostrutture di materiali semiconduttori neanche particolarmente ripuliti e raffinati, per esempio Arseniuro di Gallio (GaAs).
Con la quantizzazione si può avere una grandissima precisione (salvo possibili errori sempre in agguato): quella ottenuta arriva oggi a 10 cifre decimali. È come accorgersi della presenza o assenza di un individuo tra tutta l'umanità intera, che ormai ammonta a circa 7 miliardi di persone.
Come con i bistabili, la quantizzazione permette una digitalizzazione e quindi una grande precisione, perché i numeri interi non fluttuano: 1 è 1, 2 è 2 e così via. Che la digitalizzazione permetta un calcolo preciso lo si è capito da oltre quattro millenni, quando le prime "macchine da calcolo" ( abachi , oggi esistenti nella versione di pallottolieri) iniziarono a essere usati da Sumeri e Cinesi. In altro campo, sappiamo il progresso portato dalla televisione digitale rispetto a quella analogica.
Ad esempio la figura 8 mostra un piccolo abaco portatile (una dozzina di cm di larghezza) di età imperiale romana, conservato presso il Museo Nazionale Romano e nel Seicento appartenuto (secondo K. Menninger, Number words and number symbols ) al grande scienziato e umanista Athanasius Kircher . Benché tali abachi fossero all'epoca di uso relativamente corrente nel commercio a un certo livello, pochissimi sono sopravvissuti. L' altro esemplare ora visibile è custodito presso il Cabinet des Médailles a Parigi.
All'immagine dell'abaco è affiancata in figura 9 quella di un "qubit" quantistico superconduttore , con dimensioni alla scala del milionesimo di metro (μm) e nel calcolo quantistico corrispondente grossolanamente a un elemento dell'abaco. Il calcolo quantistico poggia sulla realizzazione di strutture fisiche descritte alla scala dei nanometri (nm, miliardesimi di metro). Al qubit è arrivata la storia delle macchine da calcolo. Iniziamo quindi a navigare verso il qubit e in generale il calcolo quantistico.
Se volete farlo, dovete issare le vele della fisica quantistica. L’Appendice fornisce una sintesi dei principi di base che servono. Per poter affrontare la comprensione del calcolo quantistico, presentiamo ora gli "strumenti" di base messi a disposizione dalla natura quantistica delle interferenze tra fotoni, o delle interferenze tra elettroni in nanostrutture: "non-località", “entanglement” e “coerenza quantistica".
Non-località e entanglement
Tenetevi forte: la fisica quantistica è “non-locale”. In parole povere: agite qui, l’effetto è anche là. Questo singolare fenomeno poggia sulle stesse fondamenta dell’apparente delocalizzazione illustrata in Appendice in relazione all’esperimento della doppia fenditura.
Quando nel 1935 Erwin Schrödinger individuò l’esistenza di una “connessione quantistica non-locale” detta “ entanglement ” (traducibile in italiano come “intreccio non separabile”), Einstein la chiamò ironicamente “ spooky action at a distance ”, traducibile in italiano con “ azione fantasmatica a distanza ” e cercò di demolirla contribuendo a enunciare il cosiddetto " Paradosso di Einstein-Poldosky-Rosen ".
La denominazione di “paradosso” venne dalla sua incompatibilità con l’assunto della Teoria della Relatività Speciale (vedete Simmetrie e Relatività Speciale ), secondo il quale nessun segnale può essere trasmesso a una velocità maggiore di quella della luce. Più precisamente, esso contrastava con l’assunzione che valesse con il cosiddetto “ principio di località ”, secondo il quale oggetti distanti non possono avere istantaneamente una reciproca influenza.
Oggi sappiamo che l’entanglement va accettato come non paradossale, ma come un modo di funzionare della natura. Non è trasmissione di forze per azione a distanza, come in L'enigma dell'interazione a distanza e i "quanti" : non abbiamo parlato di alcuna proprietà che implichi un'interazione, quale sarebbe per esempio una carica elettrica. E' un puro effetto quantistico, è “non-località”.
La non-località dell’entanglement permette la formazione di grandi sistemi quantistici, ben oltre le dimensioni atomiche la cui scala è l’Angstrom (un decimo di nanometro, ossia di miliardesimi di metro).
Per ironia della sorte, o se volete per un dantesco “ contrappasso ”, ora il suddetto paradosso può essere considerato come una previsione dell’entanglement quantistico: un’azione compiuta su un elemento di un sistema quantistico costituito da elementi entangled si riflette istantaneamente sugli altri, anche se essi non sono materialmente collegati purché in “coerenza quantistica” tra loro, come sarà presto specificato. Possiamo così parlare di stato quantistico dell’intero sistema, come illustrato in Appendice per l’atomo.
La figura 10 mostra una intrigante sorta di entanglement non quantistico in un dipinto di Giuseppe Arcimboldo (1527-1593).
Coerenza quantistica
In fisica classica, uno “stato” indica qualcosa di ben distinto da altri dello sistema. In letteratura troviamo Lo strano caso del dottor Jekyll e del signor Hyde di Robert Louis Stevenson (1850-1894). In esso, il protagonista è il dottor Jekyll “e” il signor Hyde. La straordinarietà dell’immaginazione di Stevenson è che essa ha fornito una rappresentazione di una realtà psichica (lo sdoppiamento della personalità) materialmente indescrivibile. La figura 11 mostra la copertina di una recente edizione, che riporta un'illustrazione originale.
Il mondo della fisica quantistica è diverso. Il “Principio di Sovrapposizione” (esposto in Appendice) apre la strada al singolare fenomeno della “coerenza quantistica”. La coerenza quantistica di uno stato è quell'incantesimo che permette a un oggetto (quantistico) di vivere in uno stato che può essere descritto come una sovrapposizione di altri diversi stati: nel caso di due di questi, lo stato quantistico è contemporaneamente l’uno “e” l’altro.
La realtà della fisica quantistica sfugge alla nostra usuale rappresentazione materiale valida a livello macroscopico. Tuttavia, la coerenza quantistica ci fa pensare al libro di Stevenson, anche se il dottor Jekyll e il signor Hyde non sono tali allo stesso tempo.
Quanto sia grande l’incantesimo implicito nel Principio di Sovrapposizione è ben illustrato dal paradosso detto del “ gatto di Schrödinger ”: se volessimo trattare un gatto come un oggetto quantistico al pari di un elettrone (per esempio), giungeremmo al paradosso che esso potrebbe essere contemporaneamente (per sovrapposizione) nello stato di “gatto vivo” "e" in quello di “gatto morto”.
Grazie al Principio di Sovrapposizione, si ha accesso a una grande ricchezza di stati quantistici. Per fare un’analogia, uno stato “colore verde” può essere visto come sovrapposizione di uno stato “colore blu” e di uno “colore giallo” e modificando la loro proporzione si ottiene una ricca gamma di tonalità.
I dispositivi detti “qubit” (abbreviazione di “quantum bit” e parola usata anche per indicare l' unità d'informazione quantistica ) permettono di realizzare una sovrapposizione quantistica. Grazie all’entanglement, la coerenza quantistica può essere estesa a tutti i qubit che costituiscono un sistema entangled. Modificarne lo stato comporta il modificare contemporaneamente quello di tutti i qubit del sistema. Non è più come per i bistabili, che sono messi in comunicazione inviando segnali elettrici dall’uno all’altro con una velocità che ha per limite quella della luce: questo limite viene reso irrilevante. Un qubit è stato mostrato sopra in figura 9.
Accennando al discorso che svilupperemo a breve, il calcolo quantistico consiste nel modificare il suo stato iniziale secondo il calcolo da effettuare. “Leggendo” lo stato finale si ottiene il risultato cercato.
Tuttavia, una perturbazione dall’esterno può far venir meno la coerenza quantistica e fare precipitare il sistema di qubit in uno stato indesiderato e incontrollato (come nel romanzo di Stevenson l’insorgere del signor Hyde sfugge al controllo del dottor Jekyll). Una perturbazione fatale equivale all'intrusione di un “guardone” che interferisca provando a vedere cosa accade in uno stato di intimità: l’incantesimo si rompe. Manipolare lo stato quantistico nell’esecuzione del calcolo può equivalere ad un’intrusione fatale. Ma i fisici sono diventati bravissimi a eseguirlo senza rompere l’incantesimo della coerenza quantistica.
Dispositivi quantistici e nanotecnologie
I calcolatori quantistici implicano un insieme di qubit, corrispondenti ai vecchi bistabili, in coerenza quantistica tra loro grazie ad architetture che non richiedono che siano direttamente connessi tra loro per parlarsi direttamente. Grazie all’entanglement, l’individualità dei costituenti si perde e si forma un unico “stato”, sul quale si può globalmente agire mediante minimi segnali elettrici o campi magnetici, nonché singoli fotoni agenti sui diversi costituenti. Queste architetture sono possibili grazie alle nuove “ nanotecnologie ”, così dette perché implicano manipolazioni fisiche alla scala dei nanometri.
Si supera così la difficoltà delle connessioni incrociate tra transistor, presente negli attuali "chip" degli attuali calcolatori attuali e che costituisce un problema in più da risolvere materialmente un limite per la miniaturizzazione e per la velocità dei processi.
Va sottolineato che, affinché il sistema totale dei qubit mantenga nel tempo la “coerenza quantistica”, occorre quanto più possibile sopprimere le perturbazioni indotte dall’ambiente esterno e renderlo altamente stabile. L'insieme viene schermato da radiazioni indesiderate e portato a bassissime temperature nella scala assoluta (gradi Kelvin), alle quali si instaura il fenomeno della superconduttività . Del resto, già ora la miniaturizzazione dei componenti elettronici porta a surriscaldamenti che, nei calcolatori più potenti, vanno limitati raffreddando il sistema, se è il caso anche con una camicia di azoto liquido. Complessivamente, la sfida tecnologica consiste nel realizzare un insieme di qubit che mantenga la coerenza quantistica.
Calcolo quantistico
Vediamo un poco più estesamente come procede il calcolo. L'insieme dei qubit è preparato in uno “stato quantistico”. L'algoritmo (cioè la procedura) di calcolo fa evolvere questo stato fino alla configurazione finale dell’insieme, che è poi letta come risultato in uscita. Detto in poche parole, è questo il “calcolo quantistico”. Se proprio ci vogliamo appoggiare a un’analogia appartenente al mondo di tutti i giorni, pensiamo al nostro “stato di umore”. In seguito a uno stimolo esterno (nell’analogia corrisponde all’algoritmo) la stessa persona evolve in un attimo da uno stato di umore a un altro e il cambiamento è percepito (letto) dall’esterno. Senza che alcuno si sposti.
Al momento, gli algoritmi matematici che propongono funzioni di calcolo si contano sulle dita di una mano. Eccone alcuni:
• algoritmo di Shor: per la fattorizzazione in numeri primi;
• algoritmo di Grover: per l'elenco telefonico inverso ( dato un numero trovare l'utente);
• algoritmo di Deutsch-Jozsa: per la scelta (ad esempio come ottimizzare l'uso di risorse o un itinerario).
La lettura dello stato finale risultante avviene attraverso un processo di “ tomografia” , analogo a quello usato in diagnostica medica.
Presente, futuro e futuribile
Il primo calcolatore quantistico fu “ D-wave One ”, una macchina di soli 128 qubit posta sul mercato nel 2011 dalla D-wave Company a un costo di circa 10 milioni di dollari (figura 3). E’ attualmente disponibile “ D-Wave Two ”, una macchina di 512 qubit che porta Vesuvius come nome di progetto.
Lo sforzo in corso consiste nel dimostrare che un calcolatore quantistico può essere più efficiente e veloce di una macchina convenzionale. E' plausibile che in ultima istanza questo dovrà accadere come conseguenza delle proprietà della fisica quantistica: principio di sovrapposizione e entanglement: mentre un calcolatore convenzionale deve esplorare tutte le possibilità una ad una per procedere, il calcolatore quantistico contiene tutte le possibilità insieme in un solo stato e le fa evolvere in sovrapposizione fino al risultato finale.
In aggiunta alle sue potenzialità nel calcolo, l’entanglement permette anche un avanzamento della crittografia a uno stadio qualitativamente superiore all’attuale, con tutte le implicazioni di sicurezza e di pericolo che questo comporta: siamo in un mondo la cui la rete d’interessi economici, finanziari, militari è diventata così densa da destare non poche preoccupazioni, probabilmente non ancora tutte emerse. Si tratta di solo benefici per tutti? O lo sviluppo tecnologico per forza di cose su scala mondiale e senza controllo complessivo potrà dare spazio a comportamenti irresponsabili da “ apprendista stregone "? La crittografia quantistica costituisce un capitolo a parte e queste domande sono ancora senza risposta.
Si ricomincia da tre, ma …
Ora siamo agli inizi dell'era dell’Informazione Quantistica. “ Ricomincio da tre ”, dice il titolo di un film (1981), Massimo Troisi. La maggiore spinta allo sviluppo viene di nuovo da motivazioni legate alla difesa, che possono mobilitare fondi in misura incomparabilmente superiore a quelle fornite dalla pura ricerca scientifica e tecnologica. Si spera che la situazione trovi, nell’evidente complessità, un suo equilibrio, visto che gli interessi economici intrinsecamente legati all’informatica sono diventati enormi e anche i colossi dell’informatica possono investire (per esempio lo fa Google ) somme assai rilevanti nella ricerca. In sostanza, ora militari e civili lavorano intensamente per portarci nel nuovo mondo del calcolo quantistico, spiandosi a vicenda. Questo aspetto differenzia la situazione attuale da quella dei tempi di Alan Turing.
Un aspetto totalmente nuovo è la non-località dell’entanglement, in linea di principio concettualmente sconvolgente.
E, per finire
Terminiamo con la vignetta in figura 14. Essa riprende in chiave umoristica la contemporanea probabilità che avvengano eventi diversi, che caratterizza la fisica quantistica. Un esempio è fornito in Appendice con l'esperimento delle due fenditure, ove si deve accettare che una particella possa essere passata attraverso l’una o l’altra fenditura.
Fig. 14. Come va con il tuo prototipo di calcolatore quantistico?
Benissimo! Il progetto esiste simultaneamente nello stato di successo totale e di non essere neppure partito.
Posso vederlo?
Questa è una domanda problematica.
Immagine Free Republic
Collegamenti
Achille Drago, Storia dell'Informatica
ComputerHistory.it
D-Wave, Quantum Computing Primer
D-Wave, Introduction D-Wave Quantum Hardware
Schrödinger's cat: a thought experiment in quantum mechanica , TED Education video
Appendice. Come issare le vele della fisica quantistica
Per iniziare la vera navigazione verso il calcolo quantistico, mettiamo a punto alcuni concetti di base quali “stati quantistici”, “principio di sovrapposizione” e “delocalizzazione”.
I livelli energetici possibili per l’elettrone sono caratterizzati dal numero quantico n. Se vediamo le cose in un’ottica includente del protone, in corrispondenza di ognuno di questi livelli possiamo definire uno “stato quantistico” dell’insieme nucleo-elettrone. Nulla impedisce di estendere questa visione a insiemi più larghi, come atomi con più elettroni.
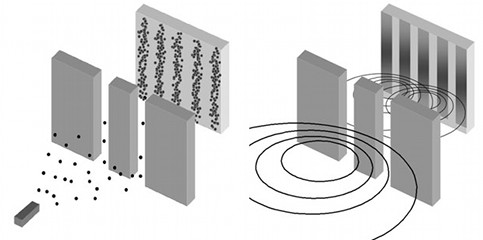
Illustriamo ora cosa s’intende in fisica quantistica per “ principio di sovrapposizione ” riferendoci al fondamentale esperimento della doppia fenditura, illustrato in Onde e particelle per pedoni molto curiosi ). Secondo la descrizione ondulatoria delle particelle, a un’energia E corrisponde una lunghezza d’onda λ = h c / E, ove c è la velocità della luce. I fenomeni quantistici si manifestano allorché la lunghezza d'onda è paragonabile alla distanza tra le fenditure. I punti d’impatto delle particelle su uno schermo posto dietro alle fenditure si dispongono allora corrispondentemente alle frange d’interferenza date dalla rappresentazione ondulatoria, come mostrato in figura A2.
Nell’interpretazione corpuscolare, non si può sapere attraverso quale delle due fenditure una particella possa essere passata ma solo le “ampiezze di probabilità” per l’una e per l’altra. Lo stato quantistico osservato sullo schermo deriva dalla “sovrapposizione” delle due possibilità, matematicamente rappresentata dalla somma delle rispettive ampiezze di probabilità. La “probabilità” ne è il quadrato”.
La fisica classica vede le particelle totalmente localizzate, ciascuna al posto suo. Nel caso della doppia fenditura, o è passata dall'una o alternativamente dall'altra. In fisica quantistica si osserva un’apparente “delocalizzazione” delle particelle, poiché lo stato quantistico contempla il passaggio sia dall’una che dall’altra fenditura. Il fenomeno è incomprensibile in termini di fisica classica: è come se potesse accadere quanto mostrato in figura A3 con il passaggio di un treno in ambedue i tunnel. Per motivi con radici profonde ancora nel mistero, in termini di ampiezza di probabilità la fisica quantistica descrive compiutamente l’apparente delocalizzazione.
................
................
Professore Associato
Dipartimento di Fisica
Università di Napoli "Federico"
Fisica delle Basse Temperature
Da Alan Turing al calcolo quantistico è stato creato da A. Tagliacozzo
Da Alan Turing al calcolo quantistico
................
................
Per domande: autori o
Domanda a un esperto
................Il moderno concetto di calcolatore, come macchina universale con un "hardware" programmabile in modo flessibile secondo le esigenze specifiche mediante un "algoritmo" implementato in un "software" (per usare termini moderni), fu introdotto dal grande matematico inglese Alan Turing nel 1936, all'età di soli 24 anni. Il suo modello paradigmatico teorico, detto " Macchina di Turing " si trova descritto in varie opere e in particolare nel libro divulgativo di Roger Penrose La mente nuova dell'imperatore , del 1989. Per quanto riguarda la storia precedente, è importante ricordare la " Macchina analitica " dello scienziato inglese Charles Babbage (1791-1871), un progetto di macchina meccanica di uso generico capace di elaborare dati immessi dall'esterno mediante schede perforate secondo un programma inserito nello stesso modo.
Fig. 1. Un convoglio di navi attaccato da un U-boot tedesco nell’attraversamento dell’Atlantico durante la Seconda Guerra Mondiale
Immagine Inilossum
Nel dicembre del 1941, in seguito al proditorio attacco giapponese a Pearl Harbour , gli Stati Uniti entrarono in guerra contro il Giappone. Questo evento fu seguito pochi giorni dopo dalla dichiarazione di guerra della Germania e dell'Italia agli Stati Uniti. Imponenti convogli di navi iniziarono ad attraversare l’Atlantico per portare soccorso all’Europa in lotta. I sottomarini tedeschi (i famigerati U-Boot ) facevano strage di navi e persone. La figura 1 mostra la drammatica immagine dell'attacco di un sommergibile tedesco a un convoglio di navi nell’attraversamento dell’Atlantico nel corso della Seconda Guerra Mondiale.
Per conoscere preventivamente ove essi fossero dislocati e pronti all'attacco e quindi potersi difendere, era essenziale entrare nel sistema di comunicazioni tedesco, che erano intercettate ma incomprensibili perché criptate in codice segreto mediante con la macchina crittografica elettromeccanica Enigma .
Alan Turing si impegnò fortemente nell'ambiziosa impresa di decriptare i codici generati da Enigma e vi riuscì, come narrato nel film The Imitation Game , uscito nel 2014. In esso si intrecciano la storia della decriptazione di Enigma e quella personale di Alan Touring, con la sua genialità e la sua problematicità.
La necessità di decriptare rapidamente i codici delle comunicazioni tedesche diede impulso allo sviluppo del calcolo elettronico. Nel 1944 fu così costruito “ Colossus ”, antesignano dei calcolatori elettronici di oggi. Colossus era una macchina elettronica basata sull'uso di “ valvole termoioniche ” in sostituzione dei “ relais ” (italianizzati in “relè”) elettromeccanici. Colossus era concettualmente basato sulla Macchina di Turing e utilizzava metodologie matematiche da lui introdotte.
Le storie della decriptazione di Enigma e di Colossus rimasero nell'ombra per decenni per motivi di segreto militare legati alla "guerra fredda" tra Occidente e blocco sovietico.
Nel 1950, con un articolo dal titolo Macchine calcolatrici e intelligenza, lo stesso Alan Turing fu anche l’iniziatore della riflessione sulla "intelligenza artificiale" rispondendo a un interrogativo, che in parole correnti può essere formulato come "potranno un giorno le macchine pensare?". Con lo spettacolare sviluppo dei robot, questa interrogativo è di grande attualità.
Le figure 2 e 3 mostrano Colossus e il "circuito integrato" del calcolatore quantistico dei nostri tempi D-Wave One. Le due macchine sono separate nel tempo da una settantina d'anni di impressionante progresso scientifico e tecnologico, del quale daremo una sintesi panoramica.
| ..........................................
Fig. 2. Il calcolatore Colossus Mark 2 nel 1943 Immagine Wikipedia | ..... | ..............................................
Fig. 3. Il calcolatore quantistico D-Wave One (2009) Immagine Wikipedia |
Le valvole termoioniche (contenute in tubi a vuoto) furono rese obsolete dall'avvento dei dispositivi a stato solido con il " transistor ". Nel 1947, ai Laboratori Bell (New Jersey, USA) fu prodotto il primo “transistor” a materiale semiconduttore (Germanio, rimpiazzato poi da Silicio e composti). Fu la nascita di un “bistabile” elettronico. Le due possibili configurazioni (denotabili con 0 e 1) permettono di codificare numeri su base "binaria" (invece che decimale). Le operazioni algebriche vengono effettuate secondo la cosiddetta “ algebra di Boole ”, la quale agisce su variabili logiche binarie ("vero" o "falso"). Il numero di bistabili determina quanti “bit” (unità d’informazione, che può valere 0 o 1) possono essere scritti ed elaborati tramite algoritmi che si materializzano in linee di trasmissione elettrica che li connettono. Due bistabili consentono di codificare i quattro numeri da zero a tre: 00,01,10,11.
Questo modo di contare a "base 2" è semplice ed essenziale, oltre che ben prestarsi al calcolo numero. Siamo abituati al conteggio a "base 10", ma la scelta è arbitraria e viene da tempi in cui non si conoscevano le motivazione teoriche e i vantaggi pratici del calcolo a base 2. Se per la vita di tutti i giorni dovessimo ora scegliere una base prossima a 10, sceglieremmo piuttosto una base multipla di due come lo è 8.
L'epopea italiana
Con la Olivetti l’Italia iniziò all’avanguardia. Nel 1959 l'ingegnere italo-cinese Mario Tchou , talento eccezionale scoperto da Adriano Olivetti , ideò la macchina “ Elea 9003 ” (la terza della serie, figura 4) disegnata nelle forme dall’architetto Ettore Sottsass . Fu il primo elaboratore “ mainframe ” (cioè a sistema centrale, generalmente di grandi dimensioni), tutto a transistor. ELEA significa “Elaboratore ELettronico Aritmetico” (o “Automatico”), ma rimanda alla scuola filosofica Eleatica secondo la quale anche l’uomo ha accesso alla verità e non solo gli Dei. E' divertente e interessante notare che recentemente il paradosso di Zenone di Elea su Achille e la tartaruga è in auge nello studio interpretativo, mai completo, della Fisica Quantistica. Inoltre, la Programma 101 (figura 5) della Olivetti fu il primo calcolatore da tavolo programmabile del mondo, posto in commercio nel 1965. Per riferimento ricordiamo che Apple I uscì nel 1976, approfittando dell'era della "microelettronica" (vedete a breve) e con importanti innovazioni comprendenti in primo luogo l'aggiunta di un visore,
| ........................................
Fig. 4. L’ELEA 9003 della Olivetti Immagine Museo Dinamico della Tecnologia A. Olivetti | ….. | .......................................
Fig. 5. La Programma 101 della Olivetti Immagine Museo Nazionale della Scienza e della Tecnologia L. da Vinci |
Nel 1960 muore improvvisamente Adriano Olivetti , all'età di 59 anni. L'anno dopo, in un incidente stradale mentre si spostava da un laboratorio a un altro, muore a solo 37 anni Mario Tchou col suo autista, scontrandosi contro un camion in circostanze mai chiarite. Finisce così l'avventura italiana nei calcolatori elettronici. Essa è narrata dalla RAI-TV nelle due puntate di “ La forza di un sogno ” insieme ad altri aspetti dell’epopea di Adriano Olivetti, che ha spaziato dal campo tecnico e industriale a quello sociale e a quello culturale. Nel 1964 l’Olivetti deve cedere la Divisione Elettronica , che passa alla General Electric per poi essenzialmente scomparire. Con il dissolversi della struttura e delle sinergie formatesi al suo interno, un inestimabile capitale d'ingegno intellettuale viene disperso anche a beneficio della californiana "Silicon Valley" come presto vedremo. Resta la Società Generale Semiconduttori fondata in quei tempi, l'attuale STMicroelectronics.
D’altro canto, nel 1962 muore in circostanze perlomeno estremamente sospette e all'età di 56 anni un altro grande protagonista dell'avanzata italiana in un settore strategico: Enrico Mattei , che con l'ENI aveva osato sfidare le grandi potenze mondiali in campo petrolifero. Furono duri colpi per la crescita tecnologica e industriale dell'Italia in aspetti strategici negli anni del cosiddetto " miracolo economico italiano " avvenuto nel dopoguerra.
A testimoniare lo stato di eccellenza raggiunto dall'Italia in quei tempi, va anche ricordato Eduardo Caianiello , uno dei pionieri delle " reti neurali " per l'apprendimento e il riconoscimento mediante intelligenza artificiale. Rientrato nel 1956 in Italia dall'Università di Princeton, fondatore e direttore dell'Istituto di Fisica Teorica e Nucleare dell'Università di Napoli in un periodo di grande fervore intellettuale, nel 1968 egli fonda l'Istituto di Cibernetica del CNR ad Arco Felice presso Pozzuoli, che vari decenni dopo sarà trasferito presso la fabbrica Olivetti di Pozzuoli ormai non più produttiva.
Questa è storia passata, seppellita dallo sviluppo tumultuoso e irrefrenabile degli ultimi 40 anni.
Entra in gioco la microelettronica
Verso la fine degli anni ’50 sono prodotti i primi “ circuiti integrati ”. In essi i vari componenti, tra i quali i transistors, sono formati tutti assieme su una sola placchetta tramite un unico processo fisico-chimico. Il dispositivo elettronico a stato solido nel suo complesso è comunemente detto “chip”, in italiano “fettina”. Nasce così la “microelettronica”. Essa è basata sulle “microtecnologie” e i suoi dispositivi hanno dimensioni misurate in micron (μm un milionesimo di metro).
I nostri attuali calcolatori utilizzano “microprocessori”. Il primo a essere commercializzato fu l’ Intel 4004 , nel 1971. Come i successivi microprocessori Intel esso fu realizzato da Federico Faggin , cresciuto nella fucina intellettuale Olivetti (di cui sopra) e poi pioniere della californiana “Silicon Valley". La figura 6 mostra gli strati superiori interconnessi del circuito integrato del microprocessore Intel 80486. La figura 7 mostra l’ Intel 8742 , che include un insieme di diversi componenti.
|
Fig. 6. Gli strati superiori interconnessi del circuito integrato del microprocessore Intel 80486 Immagine Wikiwand | ..... |
Fig. 7. Il microprocessore Intel 8742 Immagine Wikiwand |
Con la microelettronica siamo scesi a una scala dimensionale di 30 nanometri (miliardesimi di metro), dove un atomo di Silicio ha un diametro di circa 0.2 nanometri. Nel 2020 i transistor avranno solo pochi atomi. Allo sviluppo dei microdispositivi a stato solido consegue un'impressionante riduzione delle dimensioni.
Con le dimensioni diminuiscono anche i tempi di cambiamento di stato e di trasmissione dei segnali, e cresce la velocità di operazione. La velocità massima del Pentium 4 (anno 2000) era di 1066 mega-data-transfers (milioni di trasferimenti di dati) per secondo e oggi si può arrivare ad almeno a 10.000 volte di più.
Il numero di transistors su un circuito integrato supera ormai il miliardo e si raddoppia all’incirca ogni due anni seguendo la cosiddetta “ legge di Moore ”, di carattere puramente empirico. Al crescere del numero di transistors sul circuito integrato, il costo unitario decresce ma cresce anche la possibilità che esso sia difettato e non funzioni.
D'altra parte, la capacità dei dischi rigidi che servono per immagazzinare le informazioni cresce nel tempo con una velocità circa pari a quella con cui cresce il numero di transistors.
Verso il calcolo quantistico
Con le tecniche attuali, la velocità è limitata dal consumo di energia e dal riscaldamento (le ventole dei nostri calcolatori portatili ormai affannano). Inoltre il collegare tra loro i chip e le memorie implica un tempo di propagazione del segnale: anche la velocità della luce sta diventando “lenta” per noi. Una straordinaria innovazione tecnologica è però alle porte, essendo ora all'inizio di nuova avventura: quella del “calcolo quantistico”. La fisica quantistica si è sviluppata lungo tutto il secolo scorso e siamo ormai giunti alla fabbricazione e al controllo di dispositivi quantistici di crescente raffinatezza. Le tre caratteristiche del nuovo mondo dei calcolatori quantistici saranno i nuovi materiali, la necessità di super-raffreddarli e le ridottissime dimensioni.
“Quantizzare” vuol dire ammettere grandezze che variano solo a salti e non in modo continuo. In particolare, in base al cosiddetto “ Effetto Hall quantistico ” si costruiscono dispositivi la cui “conduttanza” (l’inverso di una resistenza, e normalmente misurata in Ohm -1) procede per micro-salti di e 2/ h, ove e è carica dell'elettrone e h la “ costante di Planck ” che regge la fisica quantistica. Si noti questi dispositivi possono usare nanostrutture di materiali semiconduttori neanche particolarmente ripuliti e raffinati, per esempio Arseniuro di Gallio (GaAs).
Con la quantizzazione si può avere una grandissima precisione (salvo possibili errori sempre in agguato): quella ottenuta arriva oggi a 10 cifre decimali. È come accorgersi della presenza o assenza di un individuo tra tutta l'umanità intera, che ormai ammonta a circa 7 miliardi di persone.
Come con i bistabili, la quantizzazione permette una digitalizzazione e quindi una grande precisione, perché i numeri interi non fluttuano: 1 è 1, 2 è 2 e così via. Che la digitalizzazione permetta un calcolo preciso lo si è capito da oltre quattro millenni, quando le prime "macchine da calcolo" ( abachi , oggi esistenti nella versione di pallottolieri) iniziarono a essere usati da Sumeri e Cinesi. In altro campo, sappiamo il progresso portato dalla televisione digitale rispetto a quella analogica.
| ................................................................
Fig. 8. Abaco portatile in bronzo di epoca imperiale romana Museo Nazionale Romano, Palazzo Massimo, Roma Immagine PTE Elettronica | ... | .......................................
Fig. 9. Un qubit quantistico superconduttore Royal Holloway, University of London Immagine Wikiwand |
Ad esempio la figura 8 mostra un piccolo abaco portatile (una dozzina di cm di larghezza) di età imperiale romana, conservato presso il Museo Nazionale Romano e nel Seicento appartenuto (secondo K. Menninger, Number words and number symbols ) al grande scienziato e umanista Athanasius Kircher . Benché tali abachi fossero all'epoca di uso relativamente corrente nel commercio a un certo livello, pochissimi sono sopravvissuti. L' altro esemplare ora visibile è custodito presso il Cabinet des Médailles a Parigi.
All'immagine dell'abaco è affiancata in figura 9 quella di un "qubit" quantistico superconduttore , con dimensioni alla scala del milionesimo di metro (μm) e nel calcolo quantistico corrispondente grossolanamente a un elemento dell'abaco. Il calcolo quantistico poggia sulla realizzazione di strutture fisiche descritte alla scala dei nanometri (nm, miliardesimi di metro). Al qubit è arrivata la storia delle macchine da calcolo. Iniziamo quindi a navigare verso il qubit e in generale il calcolo quantistico.
Se volete farlo, dovete issare le vele della fisica quantistica. L’Appendice fornisce una sintesi dei principi di base che servono. Per poter affrontare la comprensione del calcolo quantistico, presentiamo ora gli "strumenti" di base messi a disposizione dalla natura quantistica delle interferenze tra fotoni, o delle interferenze tra elettroni in nanostrutture: "non-località", “entanglement” e “coerenza quantistica".
Non-località e entanglement
Tenetevi forte: la fisica quantistica è “non-locale”. In parole povere: agite qui, l’effetto è anche là. Questo singolare fenomeno poggia sulle stesse fondamenta dell’apparente delocalizzazione illustrata in Appendice in relazione all’esperimento della doppia fenditura.
Quando nel 1935 Erwin Schrödinger individuò l’esistenza di una “connessione quantistica non-locale” detta “ entanglement ” (traducibile in italiano come “intreccio non separabile”), Einstein la chiamò ironicamente “ spooky action at a distance ”, traducibile in italiano con “ azione fantasmatica a distanza ” e cercò di demolirla contribuendo a enunciare il cosiddetto " Paradosso di Einstein-Poldosky-Rosen ".
La denominazione di “paradosso” venne dalla sua incompatibilità con l’assunto della Teoria della Relatività Speciale (vedete Simmetrie e Relatività Speciale ), secondo il quale nessun segnale può essere trasmesso a una velocità maggiore di quella della luce. Più precisamente, esso contrastava con l’assunzione che valesse con il cosiddetto “ principio di località ”, secondo il quale oggetti distanti non possono avere istantaneamente una reciproca influenza.
Oggi sappiamo che l’entanglement va accettato come non paradossale, ma come un modo di funzionare della natura. Non è trasmissione di forze per azione a distanza, come in L'enigma dell'interazione a distanza e i "quanti" : non abbiamo parlato di alcuna proprietà che implichi un'interazione, quale sarebbe per esempio una carica elettrica. E' un puro effetto quantistico, è “non-località”.
La non-località dell’entanglement permette la formazione di grandi sistemi quantistici, ben oltre le dimensioni atomiche la cui scala è l’Angstrom (un decimo di nanometro, ossia di miliardesimi di metro).
Per ironia della sorte, o se volete per un dantesco “ contrappasso ”, ora il suddetto paradosso può essere considerato come una previsione dell’entanglement quantistico: un’azione compiuta su un elemento di un sistema quantistico costituito da elementi entangled si riflette istantaneamente sugli altri, anche se essi non sono materialmente collegati purché in “coerenza quantistica” tra loro, come sarà presto specificato. Possiamo così parlare di stato quantistico dell’intero sistema, come illustrato in Appendice per l’atomo.
La figura 10 mostra una intrigante sorta di entanglement non quantistico in un dipinto di Giuseppe Arcimboldo (1527-1593).
| ................................................................
Fig. 10. Giuseppe Arcimboldo Le quattro stagioni: estate (1572) Kunsthistorisches Museum, Vienna Immagine Wikipedia | ….... | .......................................
Fig. 11. Robert Louis Stevenson Lo strano caso del dottor Jekyll e del signor Hyde (1886) Edizione Penguin Books - De Agostini (2004) Immagine Postcardcult |
Coerenza quantistica
In fisica classica, uno “stato” indica qualcosa di ben distinto da altri dello sistema. In letteratura troviamo Lo strano caso del dottor Jekyll e del signor Hyde di Robert Louis Stevenson (1850-1894). In esso, il protagonista è il dottor Jekyll “e” il signor Hyde. La straordinarietà dell’immaginazione di Stevenson è che essa ha fornito una rappresentazione di una realtà psichica (lo sdoppiamento della personalità) materialmente indescrivibile. La figura 11 mostra la copertina di una recente edizione, che riporta un'illustrazione originale.
Il mondo della fisica quantistica è diverso. Il “Principio di Sovrapposizione” (esposto in Appendice) apre la strada al singolare fenomeno della “coerenza quantistica”. La coerenza quantistica di uno stato è quell'incantesimo che permette a un oggetto (quantistico) di vivere in uno stato che può essere descritto come una sovrapposizione di altri diversi stati: nel caso di due di questi, lo stato quantistico è contemporaneamente l’uno “e” l’altro.
La realtà della fisica quantistica sfugge alla nostra usuale rappresentazione materiale valida a livello macroscopico. Tuttavia, la coerenza quantistica ci fa pensare al libro di Stevenson, anche se il dottor Jekyll e il signor Hyde non sono tali allo stesso tempo.
Quanto sia grande l’incantesimo implicito nel Principio di Sovrapposizione è ben illustrato dal paradosso detto del “ gatto di Schrödinger ”: se volessimo trattare un gatto come un oggetto quantistico al pari di un elettrone (per esempio), giungeremmo al paradosso che esso potrebbe essere contemporaneamente (per sovrapposizione) nello stato di “gatto vivo” "e" in quello di “gatto morto”.
Grazie al Principio di Sovrapposizione, si ha accesso a una grande ricchezza di stati quantistici. Per fare un’analogia, uno stato “colore verde” può essere visto come sovrapposizione di uno stato “colore blu” e di uno “colore giallo” e modificando la loro proporzione si ottiene una ricca gamma di tonalità.
I dispositivi detti “qubit” (abbreviazione di “quantum bit” e parola usata anche per indicare l' unità d'informazione quantistica ) permettono di realizzare una sovrapposizione quantistica. Grazie all’entanglement, la coerenza quantistica può essere estesa a tutti i qubit che costituiscono un sistema entangled. Modificarne lo stato comporta il modificare contemporaneamente quello di tutti i qubit del sistema. Non è più come per i bistabili, che sono messi in comunicazione inviando segnali elettrici dall’uno all’altro con una velocità che ha per limite quella della luce: questo limite viene reso irrilevante. Un qubit è stato mostrato sopra in figura 9.
Accennando al discorso che svilupperemo a breve, il calcolo quantistico consiste nel modificare il suo stato iniziale secondo il calcolo da effettuare. “Leggendo” lo stato finale si ottiene il risultato cercato.
Tuttavia, una perturbazione dall’esterno può far venir meno la coerenza quantistica e fare precipitare il sistema di qubit in uno stato indesiderato e incontrollato (come nel romanzo di Stevenson l’insorgere del signor Hyde sfugge al controllo del dottor Jekyll). Una perturbazione fatale equivale all'intrusione di un “guardone” che interferisca provando a vedere cosa accade in uno stato di intimità: l’incantesimo si rompe. Manipolare lo stato quantistico nell’esecuzione del calcolo può equivalere ad un’intrusione fatale. Ma i fisici sono diventati bravissimi a eseguirlo senza rompere l’incantesimo della coerenza quantistica.
Dispositivi quantistici e nanotecnologie
I calcolatori quantistici implicano un insieme di qubit, corrispondenti ai vecchi bistabili, in coerenza quantistica tra loro grazie ad architetture che non richiedono che siano direttamente connessi tra loro per parlarsi direttamente. Grazie all’entanglement, l’individualità dei costituenti si perde e si forma un unico “stato”, sul quale si può globalmente agire mediante minimi segnali elettrici o campi magnetici, nonché singoli fotoni agenti sui diversi costituenti. Queste architetture sono possibili grazie alle nuove “ nanotecnologie ”, così dette perché implicano manipolazioni fisiche alla scala dei nanometri.
Si supera così la difficoltà delle connessioni incrociate tra transistor, presente negli attuali "chip" degli attuali calcolatori attuali e che costituisce un problema in più da risolvere materialmente un limite per la miniaturizzazione e per la velocità dei processi.
Va sottolineato che, affinché il sistema totale dei qubit mantenga nel tempo la “coerenza quantistica”, occorre quanto più possibile sopprimere le perturbazioni indotte dall’ambiente esterno e renderlo altamente stabile. L'insieme viene schermato da radiazioni indesiderate e portato a bassissime temperature nella scala assoluta (gradi Kelvin), alle quali si instaura il fenomeno della superconduttività . Del resto, già ora la miniaturizzazione dei componenti elettronici porta a surriscaldamenti che, nei calcolatori più potenti, vanno limitati raffreddando il sistema, se è il caso anche con una camicia di azoto liquido. Complessivamente, la sfida tecnologica consiste nel realizzare un insieme di qubit che mantenga la coerenza quantistica.
Calcolo quantistico
Vediamo un poco più estesamente come procede il calcolo. L'insieme dei qubit è preparato in uno “stato quantistico”. L'algoritmo (cioè la procedura) di calcolo fa evolvere questo stato fino alla configurazione finale dell’insieme, che è poi letta come risultato in uscita. Detto in poche parole, è questo il “calcolo quantistico”. Se proprio ci vogliamo appoggiare a un’analogia appartenente al mondo di tutti i giorni, pensiamo al nostro “stato di umore”. In seguito a uno stimolo esterno (nell’analogia corrisponde all’algoritmo) la stessa persona evolve in un attimo da uno stato di umore a un altro e il cambiamento è percepito (letto) dall’esterno. Senza che alcuno si sposti.
Al momento, gli algoritmi matematici che propongono funzioni di calcolo si contano sulle dita di una mano. Eccone alcuni:
• algoritmo di Shor: per la fattorizzazione in numeri primi;
• algoritmo di Grover: per l'elenco telefonico inverso ( dato un numero trovare l'utente);
• algoritmo di Deutsch-Jozsa: per la scelta (ad esempio come ottimizzare l'uso di risorse o un itinerario).
La lettura dello stato finale risultante avviene attraverso un processo di “ tomografia” , analogo a quello usato in diagnostica medica.
Presente, futuro e futuribile
Il primo calcolatore quantistico fu “ D-wave One ”, una macchina di soli 128 qubit posta sul mercato nel 2011 dalla D-wave Company a un costo di circa 10 milioni di dollari (figura 3). E’ attualmente disponibile “ D-Wave Two ”, una macchina di 512 qubit che porta Vesuvius come nome di progetto.
Lo sforzo in corso consiste nel dimostrare che un calcolatore quantistico può essere più efficiente e veloce di una macchina convenzionale. E' plausibile che in ultima istanza questo dovrà accadere come conseguenza delle proprietà della fisica quantistica: principio di sovrapposizione e entanglement: mentre un calcolatore convenzionale deve esplorare tutte le possibilità una ad una per procedere, il calcolatore quantistico contiene tutte le possibilità insieme in un solo stato e le fa evolvere in sovrapposizione fino al risultato finale.
In aggiunta alle sue potenzialità nel calcolo, l’entanglement permette anche un avanzamento della crittografia a uno stadio qualitativamente superiore all’attuale, con tutte le implicazioni di sicurezza e di pericolo che questo comporta: siamo in un mondo la cui la rete d’interessi economici, finanziari, militari è diventata così densa da destare non poche preoccupazioni, probabilmente non ancora tutte emerse. Si tratta di solo benefici per tutti? O lo sviluppo tecnologico per forza di cose su scala mondiale e senza controllo complessivo potrà dare spazio a comportamenti irresponsabili da “ apprendista stregone "? La crittografia quantistica costituisce un capitolo a parte e queste domande sono ancora senza risposta.
Si ricomincia da tre, ma …
Ora siamo agli inizi dell'era dell’Informazione Quantistica. “ Ricomincio da tre ”, dice il titolo di un film (1981), Massimo Troisi. La maggiore spinta allo sviluppo viene di nuovo da motivazioni legate alla difesa, che possono mobilitare fondi in misura incomparabilmente superiore a quelle fornite dalla pura ricerca scientifica e tecnologica. Si spera che la situazione trovi, nell’evidente complessità, un suo equilibrio, visto che gli interessi economici intrinsecamente legati all’informatica sono diventati enormi e anche i colossi dell’informatica possono investire (per esempio lo fa Google ) somme assai rilevanti nella ricerca. In sostanza, ora militari e civili lavorano intensamente per portarci nel nuovo mondo del calcolo quantistico, spiandosi a vicenda. Questo aspetto differenzia la situazione attuale da quella dei tempi di Alan Turing.
Un aspetto totalmente nuovo è la non-località dell’entanglement, in linea di principio concettualmente sconvolgente.
| ..................................................................
Fig. 13. Massimo Troisi in Ricomincio da tre (1971) Immagini YouTube | ...... | ....................................... Si pensi alla cosiddetta “ noetica ” (etimologicamente riconducibile al greco “νόυς, nous”, ossia intelletto), nel cui ambito si situa l'esoterica domanda se e come la mente umana (o una mente artificiale) possa mai influenzare l’ambiente fisico. Nel suddetto film Ricomincio da tre, Massimo Troisi cercava (figura 13) di far venire a sé oggetti quali un vaso o un secchio con la forza del pensiero, quale prova di un metodo per risolvere i suoi problemi e in primo luogo quelli economici: la non-località entra anche nell’immaginazione umana, in assenza di altre risorse. Tuttavia, da pure fantasticherie, le sequenze del film potrebbero diventare divertenti illustrazioni di un nuovo capitolo della Scienza basato sulla non-località quantistica. |
E, per finire
Terminiamo con la vignetta in figura 14. Essa riprende in chiave umoristica la contemporanea probabilità che avvengano eventi diversi, che caratterizza la fisica quantistica. Un esempio è fornito in Appendice con l'esperimento delle due fenditure, ove si deve accettare che una particella possa essere passata attraverso l’una o l’altra fenditura.
Fig. 14. Come va con il tuo prototipo di calcolatore quantistico?
Benissimo! Il progetto esiste simultaneamente nello stato di successo totale e di non essere neppure partito.
Posso vederlo?
Questa è una domanda problematica.
Immagine Free Republic
Collegamenti
Achille Drago, Storia dell'Informatica
ComputerHistory.it
D-Wave, Quantum Computing Primer
D-Wave, Introduction D-Wave Quantum Hardware
Schrödinger's cat: a thought experiment in quantum mechanica , TED Education video
Appendice. Come issare le vele della fisica quantistica
Per iniziare la vera navigazione verso il calcolo quantistico, mettiamo a punto alcuni concetti di base quali “stati quantistici”, “principio di sovrapposizione” e “delocalizzazione”.
| ........................................................................
Fig. A1. Le orbite stazionarie dell’elettrone nell’atomo di Bohr secondo l’ipotesi ondulatoria Immagine Univ. Wisconsin Platteville | …..... | ....................................... Vediamo il concetto di “stato quantistico” riferendoci alla struttura atomica nella sua descrizione più semplice, formulata nel 1913 da Niels Bohr e presentata in Da linee di Fraunhofer ad atomo quantistico . Essa vale solo per l’atomo di Idrogeno e non tiene conto dello “spin”, del quale tratta una serie di articoli tra i Saggi tematici e in particolare Lo spin . Tuttavia, il “ modello di Bohr ” permette di illustrare un concetto di validità generale come quello a cui ora ci rivolgiamo. Il modello di Bohr prevede che l’elettrone sia vincolato a mantenersi su orbite fisse, corrispondenti a un momento angolare quantizzato e multiplo di h / 2p, ove p è la quantità di moto. Nella descrizione ondulatoria dell’elettrone, queste orbite corrispondono a onde stazionarie (cioè ripetute a ogni rivoluzione), come mostrato in figura A1. |
I livelli energetici possibili per l’elettrone sono caratterizzati dal numero quantico n. Se vediamo le cose in un’ottica includente del protone, in corrispondenza di ognuno di questi livelli possiamo definire uno “stato quantistico” dell’insieme nucleo-elettrone. Nulla impedisce di estendere questa visione a insiemi più larghi, come atomi con più elettroni.
Illustriamo ora cosa s’intende in fisica quantistica per “ principio di sovrapposizione ” riferendoci al fondamentale esperimento della doppia fenditura, illustrato in Onde e particelle per pedoni molto curiosi ). Secondo la descrizione ondulatoria delle particelle, a un’energia E corrisponde una lunghezza d’onda λ = h c / E, ove c è la velocità della luce. I fenomeni quantistici si manifestano allorché la lunghezza d'onda è paragonabile alla distanza tra le fenditure. I punti d’impatto delle particelle su uno schermo posto dietro alle fenditure si dispongono allora corrispondentemente alle frange d’interferenza date dalla rappresentazione ondulatoria, come mostrato in figura A2.
Nell’interpretazione corpuscolare, non si può sapere attraverso quale delle due fenditure una particella possa essere passata ma solo le “ampiezze di probabilità” per l’una e per l’altra. Lo stato quantistico osservato sullo schermo deriva dalla “sovrapposizione” delle due possibilità, matematicamente rappresentata dalla somma delle rispettive ampiezze di probabilità. La “probabilità” ne è il quadrato”.
| ........................................
Fig. A2. L’effetto della doppia fenditura secondo l’interpretazione corpuscolare (a sinistra) e quella ondulatoria (a destra) Immagine Blacklight Power | ….. | .......................................
Fig. A3. L’effetto osservato con una doppia fenditura, se esistesse solo la fisica classica Immagine The Mysearch Website |
La fisica classica vede le particelle totalmente localizzate, ciascuna al posto suo. Nel caso della doppia fenditura, o è passata dall'una o alternativamente dall'altra. In fisica quantistica si osserva un’apparente “delocalizzazione” delle particelle, poiché lo stato quantistico contempla il passaggio sia dall’una che dall’altra fenditura. Il fenomeno è incomprensibile in termini di fisica classica: è come se potesse accadere quanto mostrato in figura A3 con il passaggio di un treno in ambedue i tunnel. Per motivi con radici profonde ancora nel mistero, in termini di ampiezza di probabilità la fisica quantistica descrive compiutamente l’apparente delocalizzazione.
................
................
Professore Associato
Dipartimento di Fisica
Università di Napoli "Federico"
Fisica delle Basse Temperature
Ultima Modifica 5 Anni 1 Mese fa da Paolo.
Si prega Accesso a partecipare alla conversazione.
6 Anni 2 Settimane fa #181
da Paolo
Risposta da Paolo al topic Da Alan Turing al calcolo quantistico
A. Tagliacozzo ha scritto:
Da Alan Turing al calcolo quantistico................ ................Per domande: autori o Domanda a un esperto................
Il moderno concetto di calcolatore, come macchina universale con un "hardware" programmabile in modo flessibile secondo le esigenze specifiche mediante un "algoritmo" implementato in un "software" (per usare termini moderni), fu introdotto dal grande matematico inglese Alan Turing nel 1936, all'età di soli 24 anni. Il suo modello paradigmatico teorico, detto " Macchina di Turing " si trova descritto in varie opere e in particolare nel libro divulgativo di Roger Penrose La mente nuova dell'imperatore , del 1989. Per quanto riguarda la storia precedente dell'Informatica, è importante ricordare la " Macchina analitica " dello scienziato inglese Charles Babbage (1791-1871), un progetto di macchina meccanica per un uso generico capace di operare secondo direttive fornite dall'esterno mediante schede perforate in base a dati di ingresso forniti nello stesso modo.
Fig. 1. Un convoglio di navi attaccato da un U-boot tedesco nell’attraversamento dell’Atlantico durante la Seconda Guerra Mondiale
Immagine Inilossum
Nel dicembre del 1941, in seguito al proditorio attacco giapponese a Pearl Harbour , gli Stati Uniti entrarono in guerra contro il Giappone. Questo evento fu seguito pochi giorni dopo dalla dichiarazione di guerra della Germania e dell'Italia agli Stati Uniti. Imponenti convogli di navi iniziarono ad attraversare l’Atlantico per portare soccorso all’Europa in lotta. I sottomarini tedeschi (i famigerati U-Boot ) facevano strage di navi e persone. La figura 1 mostra la drammatica immagine dell'attacco di un sommergibile tedesco a un convoglio di navi nell’attraversamento dell’Atlantico nel corso della Seconda Guerra Mondiale.
Per conoscere preventivamente ove essi fossero dislocati e pronti all'attacco e quindi potersi difendere, era essenziale entrare nel sistema di comunicazioni tedesco, che erano intercettate ma incomprensibili perché criptate in codice segreto mediante con la macchina crittografica elettromeccanica Enigma .
Alan Turing si impegnò fortemente nell'ambiziosa impresa di decriptare i codici generati da Enigma e vi riuscì, come narrato nel film The Imitation Game , uscito nel 2014. In esso si intrecciano la storia della decriptazione di Enigma e quella personale di Alan Touring, con la sua genialità e la sua problematicità.
La necessità di decriptare rapidamente i codici delle comunicazioni tedesche diede impulso allo sviluppo del calcolo elettronico. Nel 1944 fu così costruito “ Colossus ”, antesignano dei calcolatori elettronici di oggi. Colossus era una macchina elettronica basata sull'uso di “ valvole termoioniche ” in sostituzione dei “ relais ” (italianizzati in “relè”) elettromeccanici. Colossus era concettualmente basato sulla Macchina di Turing e utilizzava metodologie matematiche da lui introdotte.
Le storie della decriptazione di Enigma e di Colossus rimasero nell'ombra per decenni per motivi di segreto militare legati alla "guerra fredda" tra Occidente e blocco sovietico.
Nel 1950, con un articolo dal titolo Macchine calcolatrici e intelligenza, lo stesso Alan Turing fu anche l’iniziatore della riflessione sulla "intelligenza artificiale" rispondendo a un interrogativo, che in parole correnti può essere formulato come "potranno un giorno le macchine pensare?". Con lo spettacolare sviluppo dei robot, questa interrogativo è di grande attualità.
Le figure 2 e 3 mostrano Colossus e il "circuito integrato" del calcolatore quantistico dei nostri tempi D-Wave One. Le due macchine sono separate nel tempo da una settantina d'anni di impressionante progresso scientifico e tecnologico, del quale daremo una sintesi panoramica.
..........................................
Fig. 2. Il calcolatore Colossus Mark 2 nel 1943
Immagine Wikipedia..... ..............................................
Fig. 3. Il calcolatore quantistico D-Wave One (2009)
Immagine Wikipedia
Le valvole termoioniche (contenute in tubi a vuoto) furono rese obsolete dall'avvento dei dispositivi a stato solido con il " transistor ". Nel 1947, ai Laboratori Bell (New Jersey, USA) fu prodotto il primo “transistor” a materiale semiconduttore (Germanio, rimpiazzato poi da Silicio e composti). Fu la nascita di un “bistabile” elettronico. Le due possibili configurazioni (denotabili con 0 e 1) permettono di codificare numeri su base "binaria" (invece che decimale). Le operazioni algebriche vengono effettuate secondo la cosiddetta “ algebra di Boole ”, la quale agisce su variabili logiche binarie ("vero" o "falso"). Il numero di bistabili determina quanti “bit” (unità d’informazione, che può valere 0 o 1) possono essere scritti ed elaborati tramite algoritmi che si materializzano in linee di trasmissione elettrica che li connettono. Due bistabili consentono di codificare i quattro numeri da zero a tre: 00,01,10,11.
Questo modo di contare a "base 2" è semplice ed essenziale, oltre che ben prestarsi al calcolo numero. Siamo abituati al conteggio a "base 10", ma la scelta è arbitraria e viene da tempi in cui non si conoscevano le motivazione teoriche e i vantaggi pratici del calcolo a base 2. Se per la vita di tutti i giorni dovessimo ora scegliere una base prossima a 10, sceglieremmo piuttosto una base multipla di due come lo è 8.
L'epopea italiana
Con la Olivetti l’Italia iniziò all’avanguardia. Nel 1959 l'ingegnere italo-cinese Mario Tchou , talento eccezionale scoperto da Adriano Olivetti , ideò la macchina “ Elea 9003 ” (la terza della serie, figura 4) disegnata nelle forme dall’architetto Ettore Sottsass . Fu il primo elaboratore “ mainframe ” (cioè a sistema centrale, generalmente di grandi dimensioni), tutto a transistor. ELEA significa “Elaboratore ELettronico Aritmetico” (o “Automatico”), ma rimanda alla scuola filosofica Eleatica secondo la quale anche l’uomo ha accesso alla verità e non solo gli Dei. E' divertente e interessante notare che recentemente il paradosso di Zenone di Elea su Achille e la tartaruga è in auge nello studio interpretativo, mai completo, della Meccanica Quantistica. Inoltre, la Programma 101 (figura 5) della Olivetti fu il primo calcolatore da tavolo programmabile del mondo, posto in commercio nel 1965. Per riferimento ricordiamo che Apple I uscì nel 1976, approfittando dell'era della "microelettronica" (vedete a breve) e con importanti innovazioni comprendenti in primo luogo l'aggiunta di un visore,
........................................
Fig. 4. L’ELEA 9003 della Olivetti
Immagine Museo Dinamico della Tecnologia A. Olivetti….. .......................................
Fig. 5. La Programma 101 della Olivetti
Immagine Museo Nazionale della Scienza e della Tecnologia L. da Vinci
Nel 1960 muore improvvisamente Adriano Olivetti , all'età di 59 anni. L'anno dopo, in un incidente stradale mentre si spostava da un laboratorio a un altro, muore a solo 37 anni Mario Tchou col suo autista, scontrandosi contro un camion in circostanze mai chiarite. Finisce così l'avventura italiana nei calcolatori elettronici. Essa è narrata dalla RAI-TV nelle due puntate di “ La forza di un sogno ” insieme ad altri aspetti dell’epopea di Adriano Olivetti, che ha spaziato dal campo tecnico e industriale a quello sociale e a quello culturale. Nel 1964 l’Olivetti deve cedere la Divisione Elettronica , che passa alla General Electric per poi essenzialmente scomparire. Con il dissolversi della struttura e delle sinergie formatesi al suo interno, un inestimabile capitale d'ingegno intellettuale viene disperso anche a beneficio della californiana "Silicon Valley" come presto vedremo. Resta la Società Generale Semiconduttori fondata in quei tempi, l'attuale STMicroelectronics.
D’altro canto, nel 1962 muore in circostanze perlomeno estremamente sospette e all'età di 56 anni un altro grande protagonista dell'avanzata italiana in un settore strategico: Enrico Mattei , che con l'ENI aveva osato sfidare le grandi potenze mondiali in campo petrolifero. Furono duri colpi per la crescita tecnologica e industriale dell'Italia in aspetti strategici negli anni del cosiddetto " miracolo economico italiano " avvenuto nel dopoguerra.
A testimoniare lo stato di eccellenza raggiunto dall'Italia in quei tempi, va anche ricordato Eduardo Caianiello , uno dei pionieri delle " reti neurali " per l'apprendimento e il riconoscimento mediante intelligenza artificiale. Rientrato nel 1956 in Italia dall'Università di Princeton, fondatore e direttore dell'Istituto di Fisica Teorica e Nucleare dell'Università di Napoli in un periodo di grande fervore intellettuale, nel 1968 egli fonda l'Istituto di Cibernetica del CNR ad Arco Felice presso Pozzuoli, che vari decenni dopo sarà trasferito presso la fabbrica Olivetti di Pozzuoli ormai non più produttiva.
Questa è storia passata, seppellita dallo sviluppo tumultuoso e irrefrenabile degli ultimi 40 anni.
Entra in gioco la microelettronica
Verso la fine degli anni ’50 sono prodotti i primi “ circuiti integrati ”. In essi i vari componenti, tra i quali i transistors, sono formati tutti assieme su una sola placchetta tramite un unico processo fisico-chimico. Il dispositivo elettronico a stato solido nel suo complesso è comunemente detto “chip”, in italiano “fettina”. Nasce così la “microelettronica”. Essa è basata sulle “microtecnologie” e i suoi dispositivi hanno dimensioni misurate in micron (μm un milionesimo di metro).
I nostri attuali calcolatori utilizzano “microprocessori”. Il primo a essere commercializzato fu l’ Intel 4004 , nel 1971. Come i successivi microprocessori Intel esso fu realizzato da Federico Faggin , cresciuto nella fucina intellettuale Olivetti (di cui sopra) e poi pioniere della californiana “Silicon Valley". La figura 6 mostra gli strati superiori interconnessi del circuito integrato del microprocessore Intel 80486. La figura 7 mostra l’ Intel 8742 , che include un insieme di diversi componenti.
Fig. 6. Gli strati superiori interconnessi del circuito integrato
del microprocessore Intel 80486
Immagine Wikiwand.....
Fig. 7. Il microprocessore Intel 8742
Immagine Wikiwand
Con la microelettronica siamo scesi a una scala dimensionale di 30 nanometri (miliardesimi di metro), dove un atomo di Silicio ha un diametro di circa 0.2 nanometri. Nel 2020 i transistor avranno solo pochi atomi. Allo sviluppo dei microdispositivi a stato solido consegue un'impressionante riduzione delle dimensioni.
Con le dimensioni diminuiscono anche i tempi di cambiamento di stato e di trasmissione dei segnali, e cresce la velocità di operazione. La velocità massima del Pentium 4 (anno 2000) era di 1066 mega-data-transfers (milioni di trasferimenti di dati) per secondo e oggi si può arrivare ad almeno a 10.000 volte di più.
Il numero di transistors su un circuito integrato supera ormai il miliardo e si raddoppia all’incirca ogni due anni seguendo la cosiddetta “ legge di Moore ”, di carattere puramente empirico. Al crescere del numero di transistors sul circuito integrato, il costo unitario decresce ma cresce anche la possibilità che esso sia difettato e non funzioni.
D'altra parte, la capacità dei dischi rigidi che servono per immagazzinare le informazioni cresce nel tempo con una velocità circa pari a quella con cui cresce il numero di transistors.
Si salpa verso il calcolo quantistico
Con le tecniche attuali, la velocità è limitata dal consumo di energia e dal riscaldamento (le ventole dei nostri calcolatori portatili ormai affannano). Inoltre il collegare tra loro i chip e le memorie implica un tempo di propagazione del segnale: anche la velocità della luce sta diventando “lenta” per noi. Una straordinaria innovazione tecnologica è però alle porte, essendo ora all'inizio di nuova avventura: quella del “calcolo quantistico”. La fisica quantistica si è sviluppata lungo tutto il secolo scorso e siamo ormai giunti alla fabbricazione e al controllo di dispositivi quantistici di crescente raffinatezza. Le tre caratteristiche del nuovo mondo dei calcolatori quantistici saranno i nuovi materiali, la necessità di super-raffreddarli e le ridottissime dimensioni.
“Quantizzare” vuol dire ammettere grandezze che variano solo a salti e non in modo continuo. In particolare, in base al cosiddetto “ Effetto Hall quantistico ” si costruiscono dispositivi la cui “conduttanza” (l’inverso di una resistenza, e normalmente misurata in Ohm -1) procede per micro-salti di e 2/ h, ove e è carica dell'elettrone e h la “ costante di Planck ” che regge la fisica quantistica. Si noti questi dispositivi possono usare nanostrutture di materiali semiconduttori neanche particolarmente ripuliti e raffinati, per esempio Arseniuro di Gallio (GaAs).
Con la quantizzazione si può avere una grandissima precisione (salvo possibili errori sempre in agguato): quella ottenuta arriva oggi a 10 cifre decimali. È come accorgersi della presenza o assenza di un individuo tra tutta l'umanità intera, che ormai ammonta a circa 7 miliardi di persone.
Come con i bistabili, la quantizzazione permette una digitalizzazione e quindi una grande precisione, perché i numeri interi non fluttuano: 1 è 1, 2 è 2 e così via. Che la digitalizzazione permetta un calcolo preciso lo si è capito da oltre quattro millenni, quando le prime "macchine da calcolo" ( abachi , oggi esistenti nella versione di pallottolieri) iniziarono a essere usati da Sumeri e Cinesi. In altro campo, sappiamo il progresso portato dalla televisione digitale rispetto a quella analogica.
................................................................
Fig. 8. Abaco portatile in bronzo di epoca imperiale romana
Museo Nazionale Romano, Palazzo Massimo, Roma
Immagine PTE Elettronica... .......................................
Fig. 9. Un qubit quantistico superconduttore
Royal Holloway, University of London
Immagine Wikiwand
Ad esempio la figura 8 mostra un piccolo abaco portatile (una dozzina di cm di larghezza) di età imperiale romana, conservato presso il Museo Nazionale Romano e nel Seicento appartenuto (secondo K. Menninger, Number words and number symbols ) al grande scienziato e umanista Athanasius Kircher . Benché tali abachi fossero all'epoca di uso relativamente corrente nel commercio a un certo livello, pochissimi sono sopravvissuti. L' altro esemplare ora visibile è custodito presso il Cabinet des Médaillles a Parigi.
All'immagine dell'abaco è affiancata in figura 9 quella di un "qubit" quantistico superconduttore , con dimensioni alla scala del milionesimo di metro (μm) e nel calcolo quantistico corrispondente grossolanamente a un elemento dell'abaco. Il calcolo quantistico poggia sulla realizzazione di strutture fisiche descritte alla scala dei nanometri (nm, miliardesimi di metro). A esso è arrivata la storia delle macchine da calcolo. Iniziamo ora a navigare verso il qubit e in generale il calcolo quantistico.
Se volete farlo, dovete issare le vele della fisica quantistica. L’Appendice fornisce una sintesi dei principi di base che servono. Per poter affrontare la comprensione del calcolo quantistico, presentiamo ora gli "strumenti" di base messi a disposizione dalla natura quantistica delle interferenze tra fotoni, o delle interferenze tra elettroni in nanostrutture: "non-località", “entanglement” e “coerenza quantistica".
Non-località e entanglement
Tenetevi forte: la fisica quantistica è “non-locale”. In parole povere: agite qui, l’effetto è anche là. Questo singolare fenomeno poggia sulle stesse fondamenta dell’apparente delocalizzazione illustrata in Appendice in relazione all’esperimento della doppia fenditura.
Quando nel 1935 Erwin Schrödinger individuò l’esistenza di una “connessione quantistica non-locale” detta “ entanglement ” (traducibile in italiano come “intreccio non separabile”), Einstein la chiamò ironicamente “ spooky action at a distance ”, traducibile in italiano con “ azione fantasmatica a distanza ” e cercò di demolirla contribuendo a enunciare il cosiddetto " Paradosso di Einstein-Poldosky-Rosen ".
La denominazione di “paradosso” venne dalla sua incompatibilità con l’assunto della Teoria della Relatività Speciale (vedete Simmetrie e Relatività Speciale ), secondo il quale nessun segnale può essere trasmesso a una velocità maggiore di quella della luce. Più precisamente, esso contrastava con l’assunzione che valesse con il cosiddetto “ principio di località ”, secondo il quale oggetti distanti non possono avere istantaneamente una reciproca influenza.
Oggi sappiamo che l’entanglement va accettato come non paradossale, ma come un modo di funzionare della natura. Non è trasmissione di forze per azione a distanza, come in L'enigma dell'interazione a distanza e i "quanti" : non abbiamo parlato di alcuna proprietà che implichi un'interazione, quale sarebbe per esempio una carica elettrica. E' un puro effetto quantistico, è “non-località”.
La non-località dell’entanglement permette la formazione di grandi sistemi quantistici, ben oltre le dimensioni atomiche la cui scala è l’Angstrom (un decimo di nanometro, ossia di miliardesimi di metro).
Per ironia della sorte, o se volete per un dantesco “ contrappasso ”, ora il suddetto paradosso può essere considerato come una previsione dell’entanglement quantistico: un’azione compiuta su un elemento di un sistema quantistico costituito da elementi entangled si riflette istantaneamente sugli altri, anche se essi non sono materialmente collegati purché in “coerenza quantistica” tra loro, come sarà presto specificato. Possiamo così parlare di stato quantistico dell’intero sistema, come illustrato in Appendice per l’atomo.
La figura 10 mostra una intrigante sorta di entanglement non quantistico in un dipinto di Giuseppe Arcimboldo (1527-1593).
................................................................
Fig. 10. Giuseppe Arcimboldo
Le quattro stagioni: estate (1572)
Kunsthistorisches Museum, Vienna
Immagine Wikipedia….... .......................................
Fig. 11. Robert Louis Stevenson
Lo strano caso del dottor Jekyll e del signor Hyde (1886)
Edizione Penguin Books - De Agostini (2004)
Immagine Postcardcult
Coerenza quantistica
In fisica classica, uno “stato” indica qualcosa di ben preciso. Non solo in fisica: per esempio, una persona può essere nello stato eretto “o” sdraiato. Lo dice anche il titolo di un recente libro di Michele Serra, Gli sdraiati , riferendosi a certi adolescenti.
Ma grazie all’immaginazione, in letteratura troviamo anche Lo strano caso del dottor Jekyll e del signor Hyde di Robert Louis Stevenson (1850-1894). In esso, il protagonista è il dottor Jekyll “e” il signor Hyde. La straordinarietà dell’immaginazione di Stevenson è che essa ha fornito una rappresentazione di una realtà psichica (lo sdoppiamento della personalità) materialmente indescrivibile. La figura 11 mostra la copertina di una recente edizione, che riporta un'illustrazione originale.
Il mondo della fisica quantistica è diverso. Il “Principio di Sovrapposizione” (esposto in Appendice) apre la strada al singolare fenomeno della “coerenza quantistica”. La coerenza quantistica di uno stato è quell'incantesimo che permette a un oggetto (quantistico) di vivere in uno stato che può essere descritto come una sovrapposizione di altri diversi stati: nel caso di due di questi, lo stato quantistico è contemporaneamente l’uno “e” l’altro.
La realtà della fisica quantistica sfugge alla nostra usuale rappresentazione materiale valida a livello macroscopico. Tuttavia, la coerenza quantistica ci fa pensare al libro di Stevenson piuttosto che a quello di Serra, anche se il dottor Jekyll e il signor Hyde non sono tali allo stesso tempo..
Quanto sia grande l’incantesimo implicito nel Principio di Sovrapposizione è ben illustrato dal paradosso detto del “ gatto di Schrödinger ”: se volessimo trattare un gatto come un oggetto quantistico al pari di un elettrone (per esempio), giungeremmo al paradosso che esso potrebbe essere contemporaneamente (per sovrapposizione) nello stato di “gatto vivo” "e" in quello di “gatto morto”.
Grazie al Principio di Sovrapposizione, si ha accesso a una grande ricchezza di stati quantistici. Per fare un’analogia, uno stato “colore verde” può essere visto come sovrapposizione di uno stato “colore blu” e di uno “colore giallo” e modificando la loro proporzione si ottiene una ricca gamma di tonalità.
I dispositivi detti “qubit” (abbreviazione di “quantum bit” e parola usata anche per indicare l' unità d'informazione quantistica ) permettono di realizzare una sovrapposizione quantistica. Grazie all’entanglement, la coerenza quantistica può essere estesa a tutti i qubit che costituiscono un sistema entangled. Modificarne lo stato comporta il modificare contemporaneamente quello di tutti i qubit del sistema. Non è più come per i bistabili, che sono messi in comunicazione inviando segnali elettrici dall’uno all’altro con una velocità che ha per limite quella della luce: questo limite viene reso irrilevante. Un qubit è stato mostrato sopra in figura 9.
Accennando al discorso che svilupperemo a breve, il calcolo quantistico consiste nel modificare il suo stato iniziale secondo il calcolo da effettuare. “Leggendo” lo stato finale si ottiene il risultato cercato.
Tuttavia, una perturbazione dall’esterno può far venir meno la coerenza quantistica e fare precipitare il sistema di qubit in uno stato indesiderato e incontrollato (come nel romanzo di Stevenson l’insorgere del signor Hyde sfugge al controllo del dottor Jekyll). Una perturbazione fatale equivale all'intrusione di un “guardone” che interferisca provando a vedere cosa accade in uno stato di intimità: l’incantesimo si rompe. Manipolare lo stato quantistico nell’esecuzione del calcolo può equivalere ad un’intrusione fatale. Ma i fisici sono diventati bravissimi a eseguirlo senza rompere l’incantesimo della coerenza quantistica.
Dispositivi quantistici e nanotecnologie
I calcolatori quantistici implicano un insieme di qubit, corrispondenti ai vecchi bistabili, in coerenza quantistica tra loro grazie ad architetture che non richiedono che siano direttamente connessi tra loro per parlarsi direttamente. Grazie all’entanglement, l’individualità dei costituenti si perde e si forma un unico “stato”, sul quale si può globalmente agire mediante minimi segnali elettrici o campi magnetici, nonché singoli fotoni agenti sui diversi costituenti. Queste architetture sono possibili grazie alle nuove “ nanotecnologie ”, così dette perché implicano manipolazioni fisiche alla scala dei nanometri.
Si supera così la difficoltà delle connessioni incrociate tra transistor, presente negli attuali "chip" degli attuali calcolatori attuali e che costituisce un problema in più da risolvere materialmente un limite per la miniaturizzazione e per la velocità dei processi.
Va sottolineato che, affinché il sistema totale dei qubit mantenga nel tempo la “coerenza quantistica”, occorre quanto più possibile sopprimere le perturbazioni indotte dall’ambiente esterno e renderlo altamente stabile. L'insieme viene schermato da radiazioni indesiderate e portato a bassissime temperature nella scala assoluta (gradi Kelvin), alle quali si instaura il fenomeno della superconduttività . Del resto, già ora la miniaturizzazione dei componenti elettronici porta a surriscaldamenti che, nei calcolatori più potenti, vanno limitati raffreddando il sistema, se è il caso anche con una camicia di azoto liquido. Complessivamente, la sfida tecnologica consiste nel realizzare un insieme di qubit che mantenga la coerenza quantistica.
Calcolo quantistico
Vediamo un poco più estesamente come procede il calcolo. L'insieme dei qubit è preparato in uno “stato quantistico”. L'algoritmo (cioè la procedura) di calcolo fa evolvere questo stato fino alla configurazione finale dell’insieme, che è poi letta come risultato in uscita. Detto in poche parole, è questo il “calcolo quantistico”. Se proprio ci vogliamo appoggiare a un’analogia appartenente al mondo di tutti i giorni, pensiamo al nostro “stato di umore”. In seguito a uno stimolo esterno (nell’analogia corrisponde all’algoritmo) la stessa persona evolve in un attimo da uno stato di umore a un altro e il cambiamento è percepito (letto) dall’esterno. Senza che alcuno si sposti.
Al momento, gli algoritmi matematici che propongono funzioni di calcolo si contano sulle dita di una mano. Eccone alcuni:
• algoritmo di Shor: per la fattorizzazione in numeri primi;
• algoritmo di Grover: per l'elenco telefonico inverso ( dato un numero trovare l'utente);
• algoritmo di Deutsch-Jozsa: per la scelta (ad esempio come ottimizzare l'uso di risorse o un itinerario).
La lettura dello stato finale risultante avviene attraverso un processo di “ tomografia” , analogo a quello usato in diagnostica medica.
Presente, futuro e futuribile
Il primo calcolatore quantistico fu “ D-wave One ”, una macchina di soli 128 qubit posta sul mercato nel 2011 dalla D-wave Company a un costo di circa 10 milioni di dollari (figura 3). E’ attualmente disponibile “ D-Wave Two ”, una macchina di 512 qubit che porta Vesuvius come nome di progetto.
Lo sforzo in corso consiste nel dimostrare che un calcolatore quantistico può essere più efficiente e veloce di una macchina convenzionale. E' plausibile che in ultima istanza questo dovrà accadere come conseguenza delle proprietà della fisica quantistica: principio di sovrapposizione e entanglement: mentre un calcolatore convenzionale deve esplorare tutte le possibilità una ad una per procedere, il calcolatore quantistico contiene tutte le possibilità insieme in un solo stato e le fa evolvere in sovrapposizione fino al risultato finale.
In aggiunta alle sue potenzialità nel calcolo, l’entanglement permette anche un avanzamento della crittografia a uno stadio qualitativamente superiore all’attuale, con tutte le implicazioni di sicurezza e di pericolo che questo comporta: siamo in un mondo la cui la rete d’interessi economici, finanziari, militari è diventata così densa da destare non poche preoccupazioni, probabilmente non ancora tutte emerse. Si tratta di solo benefici per tutti? O lo sviluppo tecnologico per forza di cose su scala mondiale e senza controllo complessivo potrà dare spazio a comportamenti irresponsabili da “ apprendista stregone "? La crittografia quantistica costituisce un capitolo a parte e queste domande sono ancora senza risposta.
Si ricomincia da tre, ma …
Ora siamo agli inizi dell'era dell’Informazione Quantistica. “ Ricomincio da tre ”, dice il titolo di un film (1981), Massimo Troisi. La maggiore spinta allo sviluppo viene di nuovo da motivazioni legate alla difesa, che possono mobilitare fondi in misura incomparabilmente superiore a quelle fornite dalla pura ricerca scientifica e tecnologica. Si spera che la situazione trovi, nell’evidente complessità, un suo equilibrio, visto che gli interessi economici intrinsecamente legati all’informatica sono diventati enormi e anche i colossi dell’informatica possono investire (per esempio lo fa Google ) somme assai rilevanti nella ricerca. In sostanza, ora militari e civili lavorano intensamente per portarci nel nuovo mondo del calcolo quantistico, spiandosi a vicenda. Questo aspetto differenzia la situazione attuale da quella dei tempi di Alan Turing.
Un aspetto totalmente nuovo è la non-località dell’entanglement, in linea di principio concettualmente sconvolgente.
..................................................................
Fig. 13. Massimo Troisi in Ricomincio da tre (1971)
Immagini YouTube...... .......................................
Si pensi alla cosiddetta “ noetica ” (etimologicamente riconducibile al greco “νόυς, nous”, ossia intelletto), nel cui ambito si situa l'esoterica domanda se e come la mente umana (o una mente artificiale) possa mai influenzare l’ambiente fisico.
Nel suddetto film Ricomincio da tre, Massimo Troisi cercava (figura 13) di far venire a sé oggetti quali un vaso o un secchio con la forza del pensiero, quale prova di un metodo per risolvere i suoi problemi e in primo luogo quelli economici: la non-località entra anche nell’immaginazione umana, in assenza di altre risorse. Tuttavia, da pure fantasticherie, le sequenze del film potrebbero diventare divertenti illustrazioni di un nuovo capitolo della Scienza basato sulla non-località quantistica.
E, per finire
Terminiamo con la vignetta in figura 14. Essa riprende in chiave umoristica la contemporanea probabilità che avvengano eventi diversi, che caratterizza la fisica quantistica. Un esempio è fornito in Appendice con l'esperimento delle due fenditure, ove si deve accettare che una particella possa essere passata attraverso l’una o l’altra fenditura.
Fig. 14. Come va con il tuo prototipo di calcolatore quantistico?
Benissimo! Il progetto esiste simultaneamente nello stato di successo totale e di non essere neppure partito.
Posso vederlo?
Questa è una domanda problematica.
Immagine Free Republic
Collegamenti
Achille Drago, Storia dell'Informatica
ComputerHistory.it
D-Wave, Quantum Computing Primer
D-Wave, Introduction D-Wave Quantum Hardware
Schrödinger's cat: a thought experiment in quantum mechanica , TED Education video
Appendice. Come issare le vele della fisica quantistica
Per iniziare la vera navigazione verso il calcolo quantistico, mettiamo a punto alcuni concetti di base quali “stati quantistici”, “principio di sovrapposizione” e “delocalizzazione”.
........................................................................
Fig. A1. Le orbite stazionarie dell’elettrone
nell’atomo di Bohr secondo l’ipotesi ondulatoria
Immagine Univ. Wisconsin Platteville…..... .......................................
Vediamo il concetto di “stato quantistico” riferendoci alla struttura atomica nella sua descrizione più semplice, formulata nel 1913 da Niels Bohr e presentata in Da linee di Fraunhofer ad atomo quantistico . Essa vale solo per l’atomo di Idrogeno e non tiene conto dello “spin”, del quale tratta una serie di articoli tra i Saggi tematici e in particolare Lo spin . Tuttavia, il “ modello di Bohr ” permette di illustrare un concetto di validità generale come quello a cui ora ci rivolgiamo.
Il modello di Bohr prevede che l’elettrone sia vincolato a mantenersi su orbite fisse, corrispondenti a un momento angolare quantizzato e multiplo di h / 2p, ove p è la quantità di moto. Nella descrizione ondulatoria dell’elettrone, queste orbite corrispondono a onde stazionarie (cioè ripetute a ogni rivoluzione), come mostrato in figura A1.
I livelli energetici possibili per l’elettrone sono caratterizzati dal numero quantico n. Se vediamo le cose in un’ottica includente del protone, in corrispondenza di ognuno di questi livelli possiamo definire uno “stato quantistico” dell’insieme nucleo-elettrone. Nulla impedisce di estendere questa visione a insiemi più larghi, come atomi con più elettroni.
Illustriamo ora cosa s’intende in fisica quantistica per “ principio di sovrapposizione ” riferendoci al fondamentale esperimento della doppia fenditura, illustrato in Onde e particelle per pedoni molto curiosi ). Secondo la descrizione ondulatoria delle particelle, a un’energia E corrisponde una lunghezza d’onda λ = h c / E, ove c è la velocità della luce. I fenomeni quantistici si manifestano allorché la lunghezza d'onda è paragonabile alla distanza tra le fenditure. I punti d’impatto delle particelle su uno schermo posto dietro alle fenditure si dispongono allora corrispondentemente alle frange d’interferenza date dalla rappresentazione ondulatoria, come mostrato in figura A2.
Nell’interpretazione corpuscolare, non si può sapere attraverso quale delle due fenditure una particella possa essere passata ma solo le “ampiezze di probabilità” per l’una e per l’altra. Lo stato quantistico osservato sullo schermo deriva dalla “sovrapposizione” delle due possibilità, matematicamente rappresentata dalla somma delle rispettive ampiezze di probabilità. La “probabilità” ne è il quadrato”.
........................................
Fig. A2. L’effetto della doppia fenditura secondo l’interpretazione corpuscolare (a sinistra)
e quella ondulatoria (a destra)
Immagine Blacklight Power….. .......................................
Fig. A3. L’effetto osservato con una doppia fenditura,
se esistesse solo la fisica classica
Immagine The Mysearch Website
La fisica classica vede le particelle totalmente localizzate, ciascuna al posto suo. Nel caso della doppia fenditura, o è passata dall'una o alternativamente dall'altra. In fisica quantistica si osserva un’apparente “delocalizzazione” delle particelle, poiché lo stato quantistico contempla il passaggio sia dall’una che dall’altra fenditura. Il fenomeno è incomprensibile in termini di fisica classica: è come se potesse accadere quanto mostrato in figura A3 con il passaggio di un treno in ambedue i tunnel. Per motivi con radici profonde ancora nel mistero, in termini di ampiezza di probabilità la fisica quantistica descrive compiutamente l’apparente delocalizzazione.
................
................
Si prega Accesso a partecipare alla conversazione.
Tempo creazione pagina: 0.840 secondi