Onde e particelle per pedoni molto curiosi
- P. Strolin
-
Autore della discussione
- Offline
- Premium Utente
-
Less
Di più
13 Anni 2 Giorni fa - 5 Anni 2 Mesi fa #58
da P. Strolin
...................................................
Guardate in figura 1 la statua lignea di monaco buddista del periodo Heian (794-1185), ora affidata al Museo Nazionale di Kyoto . L’immagine nasce da una cultura figurativa in cui il valore simbolico ha un ruolo primario. Non è mera rappresentazione di una realtà materiale. E’ magica materializzazione lignea di un’immagine mentale, a sua volta frutto di una visione filosofica. Ci colpisce e attrae con suo sottile e profondo mistero. Vorreste decifrarlo?
Fig. 1. Il monaco Baozhi (Important Cultural Property)
J. Hōshi, Periodo Heian (794-1185), Tempio di Saiō-ji, Kyoto
Clic per statua intera da Museo Nazionale di Kyoto
Il sentir parlare di “ dualismo onda-particella ” ci procura un simile turbamento. Ma il mistero può essere indagato. Resterà un fondamentale mistero, ma si potrà capire come nasce, in cosa consiste e cosa implica. Vedremo che la realtà fisica è molto bella e ben diversa da quanto evoca la parola "dualismo".
Onde e particelle venivano classicamente considerate entità concettualmente separate, in alternativa. Con la fisica moderna emerge piuttosto un quadro “ olistico ”, in cui onda e particella sono inserite in una coerente visione unitaria. È come passare da una rozza differenziazione degli umani tra femmine e maschi a una visione più profonda: in termini degli orientali yin e yang , presenti in diverse proporzioni, ma sempre entro lo stesso ambito umano. Lo rappresenta il ben noto simbolo, con campi bianco e nero racchiusi in un unico cerchio.
Sono richieste conoscenze elementari di Fisica Quantistica, quali quelle esposte in Da linee di Fraunhofer ad atomo quantistico e fornite in modo sistematico in Gli atomi: il mondo quantico nel testo online La Chimica di Atkins.
Scoperta di un nuovo mondo
Il volgere dell'Ottocento e i primi decenni del Novecento segnarono l'inizio di una nuova epoca, nella Scienza come in altri aspetti della cultura umana. Per esempio, nelle arti figurative l' Impressionismo diede il via all'arte moderna e a tutte le sue evoluzioni e rivoluzioni.
Fatti sperimentali “impossibili” (secondo il pensiero vigente in quel tempo) furono elaborati grazie a un’incredibile attività intellettuale e portarono alla "Meccanica Quantistica” (vedete Da linee di Fraunhofer ad atomo quantistico ). Essa si dimostrò di capace di descrivere i fenomeni alla scala atomica, estesa a livelli inferiori grazie a successivi sviluppi. La “Meccanica Classica” resta limitata al mondo macroscopico, ove mantiene la sua validità.
Negli stessi anni fu concepita la “Teoria della Relatività”, una grandiosa costruzione intellettuale partita dal fatto sperimentale che la velocità della luce è una costante, indipendente dal sistema di riferimento. Le equazioni di Maxwell dell'elettromagnetismo classico non hanno più bisogno di nulla per giustificare l'invarianza della velocità della luce (vedete Simmetrie e Relatività Speciale e Interazione Elettromagnetica "alla Feynman" ).
Fig. 2. "Sono stanca di questa forma. Sono curiosa di sapere che cosa succederebbe se fosse rotonda"
Così fu inventata la ruota?
Liza Donnelly , The New Yorker - Immagine Rapporto annuale Pirelli 2012
Con le sue applicazioni, questa rivoluzione scientifica oggi pervade anche il quotidiano e lo farà ancor di più in futuro. E' passato un secolo e almeno i suoi fondamenti dovrebbero far parte di un patrimonio di conoscenza comune.
Qui vedremo i fondamenti della Meccanica Quantistica, in modo concettualmente accessibile a chi non possiede strumenti matematici professionali. Rivivremo le emozioni della Scienza nel collegare e sublimare in sintesi teoriche nuovi fatti sperimentali.
Nel titolo “Onde e particelle per pedoni molto curiosi” è parafrasato quello di uno storico libro di Harry Lipkin sulla "Teoria dei Gruppi" (Lie groups for pedestrians - Gruppi di Lie per pedoni) per persone non dotate di strumenti specifici). Abbiamo aggiunto "molto curiosi". Infatti, è noto da tempi immemorabili che la curiosità è un motore di conoscenza e di progresso (figura 2).
Nuovi fatti sperimentali
Le nuove teorie si basano su nuovi fatti sperimentali e/o acute interpretazioni di dati esistenti. I nuovi fatti sperimentali che si presentarono erano molto intriganti per non dire sconvolgenti. Per massima concisione citiamone due, fondamentali. Sperimentalmente si vide che le onde elettromagnetiche, quale è la luce, si possono comportare anche come particelle: nel cosiddetto "effetto fotoelettrico", esse agiscono come "quanti" cioè come particelle. D'altra parte, fu osservata la "diffrazione di elettroni" da parte di fenditure: le particelle manifestano fenomeni di interferenza tipici delle onde.
Effetto fotoelettrico: onde come particelle
Vediamo anzitutto l’ effetto fotoelettrico e la sua interpretazione quantistica, che segnarono l'inizio di una nuova visione della Fisica portando a frutto un aspetto del progresso scientifico su largo campo iniziato quasi un secolo prima con l'osservazione delle cosiddette "Linee di Fraunhofer" (vedete Da linee di Fraunhofer a Universo in-espansione e Da linee di Fraunhofer ad atomo quantistico ).
Una radiazione elettro-magnetica può essere trasmessa agli elettroni in un atomo e estrarli dall’atomo stesso. La teoria ondulatoria della radiazione elettro-magnetica, formulata da Maxwell poco dopo metà Ottocento, fa prevedere che riducendo l’intensità della radiazione si possa giungere al punto in cui essa non apporti più energia sufficiente per estrarre gli elettroni. Non è così. Il fenomeno si attenua ma persiste. Non dipende dall'intensità ma piuttosto dalla "frequenza" della radiazione.
L'interpretazione data da Albert Einstein nel 1905 fu che l’energia arriva a pacchetti, detti “quanti” (figura 3). Questo comportamento è tipico delle particelle. Diminuendo l’intensità della radiazione, si riduce solamente il flusso di quanti. L'energia E di ogni singolo quanto dipende unicamente dalla frequenza f della radiazione. Anzi è praticamente la stessa cosa. Essa è, infatti, data dalla frequenza moltiplicata per una costante h : E = h f.
La costante h era stata introdotta da Max Planck nel 1900 per spiegare la distribuzione dell'energia (spettro) trasmessa alla materia da una radiazione attraverso una "quantizzazione" dell'energia stessa, ossia l'assunzione di valori variabili "a scalino" invece che in modo continuo. Con l'interpretazione di Einstein dell'effetto fotoelettrico, essa viene associata non solo a uno scalino ma anche a un "quanto" di energia con le caratteristiche di una particella. L'innovazione concettuale èi fondamentale.
La "costante di Planck" h irrompe così prepotentemente nel mondo della Fisica, caratterizzandola al livello quantistico-ondulatorio. Si entra in un dominio di nuova Scienza. Essa ha un valore molto piccolo: h = 1,2 x 10 -13 (GeV/c) cm. I fenomeni ad essa connessi non sono quindi generalmente visibili per corpi a una scala macroscopica.
Sviluppi del pensiero scientifico, a volo d'uccello
Da linee di Fraunhofer ad atomo quantistico narra che l'aurora della comprensione della natura ondulatoria dell'elettrone, archetipo di particella elementare, venne nel 1913 con il "Modello atomico di Bohr", nel quale i livelli energetici discreti (non con valori continui) osservati per l'atomo di Idrogeno sono interpretati come effetto di una provvidenziale quantizzazione del momento angolare. L' ipotesi di una natura ondulatoria dell'elettrone sorse infine nel 1924 per opera di Louis de Broglie. Divenne così possibile associare la quantizzazione del momento angolare a orbite degli elettroni vincolate a corrispondere a " onde stazionarie ".
il " principio di indeterminazione " (1927) impose di accettare l'impossibilità di determinare contemporaneamente con qualsivoglia precisione due grandezze fisiche che nel mondo quantistico sono "correlate", quali sono la posizione e la quantità di moto di una particella o il tempo in cui è osservata e la sua energia.
Più precisamente, il prodotto delle loro indeterminazioni resta costante e il suo valore è dato dalla costante di Planck, che si si riafferma come la costante fondamentale della Fisica Quantistica: se agiamo per diminuire l'una, l'altra scappa automaticamente in su.
Accade anche nel gioco mostrato in figura 5 con una fotografia del grande captatore di istanti umani Robert Doisneau .
Fig. 5. La mariée chez Gégene (La sposa da Gégene), 1946
Robert Doisneau - Immagine Atelier Robert Doisneau
L' Equazione di Schrödinger (1926) unì natura ondulatoria e Principio di Indeterminazione sotto lo stesso tetto della costante di Planck, per descrivere il comportamento dell'elettrone. Al concetto di orbita definita e fissa del modello atomico di Bohr si sostituì quello di " orbitale ", caratterizzato da una distribuzione di probabilità.
Infine l' Equazione di Dirac - concepita nel 1927 per essere valida anche in regime relativistico - sorprendentemente incluse lo " spin " dell'elettrone e permise di tenerne conto nella descrizione degli orbitali elettronici.
L'Equazione di Dirac aprì la strada alla fisica delle particelle elementari. Essa sorprese anche con la predizione dell'esistenza di " anti-particelle ", che tuttora produce uno sconcerto acquietato solamente approfondendone la conoscenza negli aspetti teorici e sperimentali. La predizione fu confermata dalla scoperta dell'anti-elettrone ("positrone") nel 1932.
Diffrazione di elettroni: particelle come onde
In fisica classica, i fenomeni di interferenza sono caratteristici della onde e gli esperimenti su fenditure costituiscono una efficace metodologia sperimentale per osservarli. Così il celebre esperimento di Young (1803) mise in evidenza il carattere ondulatorio della luce attraverso l'osservazione di una sua diffrazione come effetto di un fenomeno di interferenza.
L' osservazione sperimentale diretta della natura ondulatoria dell'elettrone fu fornita negli anni 1925-27 da Clinton Davisson e Lester Germer nonché indipendentemente da George Paget Thomson, che ne osservarono la diffrazione su un reticolo cristallino. La figura 4 mostra che si ha un picco di interferenza costruttiva per certi angoli (50 o in figura) dipendenti dal rapporto tra la lunghezza d'onda dell'elettrone λ indicata dall' ipotesi ondulatoria di de Broglie e la distanza d tra gli atomi del reticolo, secondo una legge corrispondente alla " relazione di Bragg " della fisica classica. In figura non è mostrato il contributo all'interferenza costruttiva dato dagli strati immediatamente sottostanti del reticolo. George Thomson osservò un simile effetto diffrattivo all’attraversamento di una sottile lamina d’oro.
Onde: ampiezza e intensità
La figura 6 mostra la "ampiezza" e la "intensità" della oscillazione provocata da un'onda generica, in un dato punto dello spazio e in funzione del tempo. Per vederne il significato nella pratica, vi propongo di "pensare" a una breve uscita in mare. Il mare monta, l’altezza (che possiamo anche dire ampiezza) delle onde raddoppia, senza che per fortuna l’onda si rompa. Il timore quadruplica in intensità, perché è collegato alla grandezza fisica che caratterizza l'impatto dell'onda: l’energia trasportata dal moto ondoso. In generale, una trattazione matematica completa porta a concludere che l'intensità (sempre positiva) di un'onda è proporzionale al quadrato della sua ampiezza (oscillante). L'andar per mare può aiutare a capire la Fisica.
La doppia fenditura in esperimenti pensati
Dal punto di vista del meccanismo di formazione dell'interferenza, l'apparato di Young, il reticolo cristallino di Davisson e Germer e gli atomi nella sottile lamina d’oro di Thomson sono concettualmente equivalenti a un apparato ideale detto "doppia fenditura", implicitamente assunto di scala dimensionale atta a evidenziare fenomeni diffrattivi .
In quel capolavoro di divulgazione scientifica che è il Dialogo sopra i due massimi sistemi del mondo (pubblicato nel 1632), Galileo Galilei espone il suo concetto di relatività facendo pensare il lettore a un "navilio" all’interno del quale delle farfalle volano senza accorgersi del suo moto relativamente al mondo circostante. Potete trarre piacere dalla lettura di una trascrizione parziale del bellissimo testo di Galileo su Simmetrie e Relatività Speciale .
Il navilio di Galileo è uno storico esempio di “ esperimento pensato ” (noto con la denominazione tedesca "gedanken experiment"). Un esperimento pensato, non necessariamente realistico ma aderente alla sostanza del fenomeno, può costituire un efficace strumento per capire e far capire. Con perfida ironia, la figura 7 ne fornisce un esempio.
Le figure 8 e 9 sono tratte dalla preziosa Fisica di Feynman e rappresentano esperimenti pensati semplici e incisivi, metodologicamente basati sul concetto di esperimento con doppia fenditura applicato a onde e particelle. Seguiremo la traccia data da Richard Feynman . Vale la pena non sottrarsi al fascino della sua personalità e ascoltarne una viva lezione sull'argomento qui trattato, disponibile sul Web. Se vi capita, leggete i libri di divulgazione scientifica e qualsiasi cosa egli abbia scritto, non solo su argomenti di Fisica. Quello che accade con onde e particelle può essere visto anche in una animazione visibile sul Web, o in una fantasiosa lezione del Dr. Quantum . In italiano, sono disponibili le diapositive di un seminario "fatto in casa" e collegato a questo sito Web.
Fig. 8. Onde su fenditure (da La Fisica di Feynman)
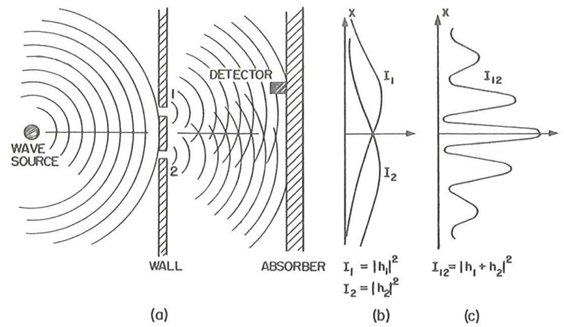
Onde elettromagnetiche su doppia fenditura
La figura 8 illustra schematicamente cosa accade quando delle onde (per ora di qualsiasi natura) investono una doppia (1 e 2) fenditura caratterizzata da una scala dimensionale a distanza paragonabile alla lunghezza d'onda. Su un piano di osservazione (absorber) oltre le fenditure, l'intensità I 12 del segnale con ambedue le fenditure aperte mostra le frange d'interferenza tipiche delle onde (c in figura . Il motivo fisico - riflesso nella struttura matematica - è che si sommano le ampiezze h
1
e h
2
(h sta per l'inglese height, altezza) del segnale con solo l'una o l'altra delle fenditure aperte, e non le rispettive intensità I
1
e I
2
(b in figura
. Il motivo fisico - riflesso nella struttura matematica - è che si sommano le ampiezze h
1
e h
2
(h sta per l'inglese height, altezza) del segnale con solo l'una o l'altra delle fenditure aperte, e non le rispettive intensità I
1
e I
2
(b in figura  .
.
Focalizziamo l'attenzione sulle onde elettromagnetiche (vedete Interazione Elettromagnetica "alla Feynman" ) e domandiamoci se questo comportamento persista quando l'intensità della sorgente è ridotta indefinitamente. A un certo punto si inizia a vedere che il segnale non è continuo. Esso arriva a colpi, sotto forma di singoli punti luminosi sul piano di osservazione se questo è uno schermo con la proprietà di emettere luce quando colpito. Si osservano singoli "quanti". I quanti osservati sono della stessa natura di quelli che provocano l'effetto fotoelettrico. Come nell'effetto fotoelettrico, la fisica classica è superata: le onde elettromagnetiche sono anche particelle, chiamate " fotoni ".
Incuriositi, continuiamo ad accumulare punti luminosi sullo schermo. Quello che accade diventa proprio incredibile. I quanti arrivano a colpi come particelle e in base alla loro concezione classica ci attenderemmo che essi attraversino l'una o l'altra fenditura, fornendo un segnale complessivo uguale a I 1 + I 2 . Non è così. I singoli quanti si distribuiscono automaticamente uno dopo l'altro in bande separate da zone vuote, e l'immagine che si va costruendo assomiglia sempre più alla classica figura di interferenza I 12 osservata per le onde. I singoli quanti mantengono anche un comportamento da onda. E' come se un singolo quanto attraversasse “ambedue” le fenditure al pari di un'onda, interferendo con sé stesso in modo che colpo dopo colpo si formino le classiche frange d'interferenza.
In sintesi, le onde elettromagnetiche sono costituite da quanti, che arrivano a colpi come particelle ma danno luogo a interferenza come onde. Per dirla come Massimo Troisi in Pensavo fosse amore... invece era un calesse , ma con ritorno di fiamma: pensavamo che fossero onde e sono particelle, e queste si comportano anche da onda. Di primo acchito possono sembrare giochi di parole e confondere. In realtà rappresentano l'integrazione dei concetti di onda e particella in un unico cerchio alla yin e yang della quale si è parlato inizialmente, abitualmente chiamata dualismo anche se questa denominazione può non contribuire alla chiarezza.
Questo per quanto riguarda il fotone, nato da un'onda come la Venere del Botticelli . Curiosità impone.di vedere come l'elettrone, nato come particella "alla Democrito ", si comporta con una doppia fenditura. Troveremo simmetria?
Fig. 9. Elettroni su fenditure (da La Fisica di Feynman)
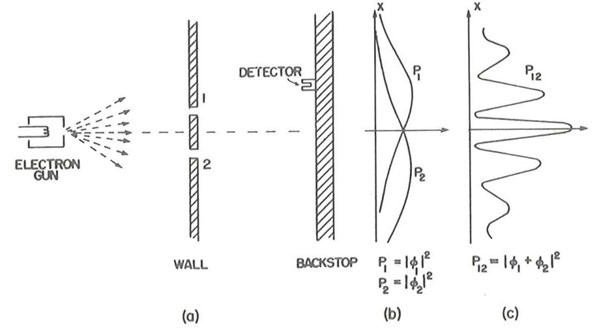
Elettroni su doppia fenditura
Rivolgiamo ora l'attenzione sulla figura 9, dove consideriamo che la doppia fenditura sia investita da particelle con credenziali doc: elettroni. Partendo da una configurazione nella quale essi si comportano da particelle, “immaginiamo" di diminuire progressivamente le fenditure in larghezza e distanza.
Abbiamo una grossa sorpresa: a un certo punto appaiono frange d’interferenza come mostrato in (c), in modo puramente indicativo. Dalla distanza tra le frange si può anche dedurre una lunghezza d’onda λ associata agli elettroni e scoprire che essa è legata all'inverso della loro quantità di moto p da una costante moltiplicativa, di nuovo la costante h di Planck: λ = h / p come nell' ipotesi ondulatoria di de Broglie. È come se lo stesso elettrone passasse attraverso ambedue le fenditure. La figura 10 mostra quanto questo sia paradossale nella visione classica: se il treno avesse un comportamento quantistico, dovrebbe tranquillamente poter passare attraverso ambedue i tunnel.
Abbiamo detto “immaginiamo” e abbiamo così approfittato dei vantaggi degli esperimenti pensati. Continuando con l'immaginazione, registriamo uno a uno l'impatto dei singoli elettroni. Come i singoli fotoni di cui sopra, vediamo gli elettroni accumularsi formando man mano frange di interferenza. Lo mostra l'animazione in figura 11, che potrebbe anche essere riferita al comportamento di singoli fotoni precedentemente descritto. Vi è simmetria tra elettroni e fotoni. Per entrambi le due rappresentazioni possono concettualmente coesistere: essi sono onde "e" particelle. La fisica classica è superata: in essa l'essere onda "oppure" particella sono mutualmente esclusivi.
È difficilissimo passare da un esperimento pensato a uno reale, con registrazione di elettroni singoli. Le fenditure devono avere dimensioni e distanze straordinariamente piccole: la grandezza di riferimento è la lunghezza d'onda di de Broglie dell'elettrone, la quale risente del piccolissimo valore della costante di Planck. Ma nel 1976 con raffinatissimi accorgimenti l’esperimento fu realmente eseguito all’Università di Bologna e fu vista l' interferenza quantistica di singoli elettroni .
Indeterminazione e probabilità: Oh Alice ... Ma Bob...
Le sorprese si aggiungono alle sorprese. Immaginiamo di riuscire, in qualche modo, a determinare da quale delle due fenditure l'elettrone sia passato: l'interferenza scompare. Se osservato, l’elettrone fa come i bambini e si comporta da "brava particella". In termini scientifici, il suo comportamento da onda è collegato alla "indeterminazione" nella fenditura dalla quale è passato. È una manifestazione del principio di indeterminazione, del quale abbiamo già parlato, Possiamo solo assegnare una "probabilità" al passaggio attraverso ciascuna delle fenditure. Due nuove parole entrano nella rigorosa Fisica al livello fondamentale: "indeterminazione" e "probabilità". Con esse, la costante h di Planck ha colpito ancora. Le certezze e realtà assolute ottocentesche - con i loro risvolti di arroganza da parte delle piccole menti - sono ora sanamente mutate in realtà probabilistiche, come in altri campi del sapere, nella vita personale e nell'evoluzione di sistemi complessi quale è per esempio la società umana: la Fisica si è umanizzata.
I paradossi fanno capire la portata rivoluzionaria di nuove visioni della Scienza, non solo in quanto qui discusso (vedete per esempio Simmetrie e Relatività Speciale ). L'ironia usa spesso lo stesso strumento, come mostra la figura 12.
Fig. 12. Oh Alice ... tu sei la sola per me
Ma Bob ... in un mondo quantistico come puoi esserne sicuro?
Immagine Physics Intuition Applications
Fisica Quantistica: probabilità
Dice Feynman nelle sue lezioni già citate parlando degli esperimenti descritti sopra, concettualmente chiamati "su doppia fenditura":
Questa sorprendente rivoluzione concettuale pose la sfida scientifica di inquadrarla in una struttura matematica coerente. Come prima cosa, che fare ora che il principio di indeterminazione ci impedisce di dire che una particella "ha" certe coordinate spaziali e una certa quantità di moto? Dobbiamo trattarla come un'onda "e" in termini probabilistici. La figura 6 viene in soccorso, dando la "dritta". In primo luogo, la probabilità deve essere sempre positiva: non può che corrispondere a quella che in fisica classica è l'intensità dell'onda, precedentemente definita come il quadrato dell'ampiezza. Sempre iniziando con un riferimento alla fisica classica, i meccanismi dei fenomeni sono descritti ragionando sull'ampiezza: come potrebbero altrimenti le intensità (sempre positive) di due onde sommarsi algebricamente e dar luogo non solo a interferenza costruttiva, ma anche distruttiva?
Fisica Quantistica: ampiezza di probabilità
Da quanto detto sopra si può capire che anche in Fisica Quantistica per la descrizione dei fenomeni si deve ragionare sull'ampiezza. Essa assume il nome di "ampiezza di probabilità" per caratterizzarne la connessione con una probabilità, data da un'operazione che nell'appropriato formalismo matematico corrisponde a un'elevazione a potenza al quadrato, proprio come per le onde in figura 6.
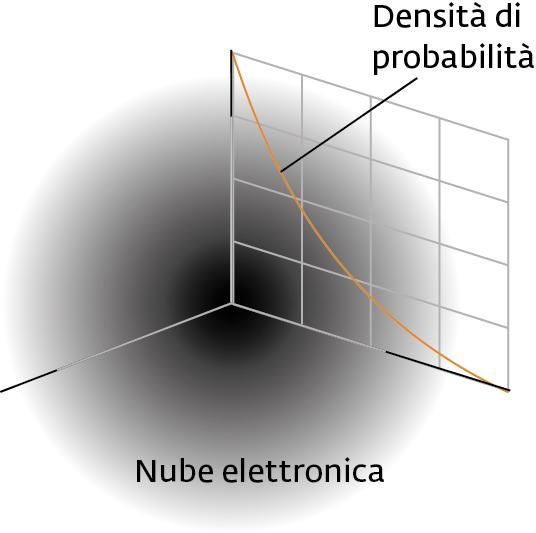
Si è precedentemente detto che il comportamento di una particella come l'elettrone è descritto dall'Equazione di Schrödinger o, in maniera più completa, dall'equazione di Dirac, Va da sè che esse operano su "ampiezze di probabilità". Le loro soluzioni sono dette " funzioni d'onda ". Lo sono gli orbitali che descrivono lo stato di un elettrone in un atomo in corrispondenza di specifici "numeri quantici" (vedete Da linee di Fraunhofer ad atomo quantistico ). Un esempio di orbitale è dato in figura 13, che mostra la distribuzione di probabilità sotto forma di "nube elettronica".
Riflettendo, un orbitale non rappresenta un elettrone singolo, ma piuttosto l'elettrone nel "sistema atomo", con funzione d'onda determinata dal legame con il nucleo. Che dire di una particella libera, elettrone, fotone o altra che sia? La figura 6 viene di nuovo in soccorso. L'onda che mostra può essere vista come rappresentazione di un caso limite contemplato dal principio di indeterminazione, ove la costante di Planck fissa il prodotto delle indeterminazioni di variabili correlate. Nella figura, la lunghezza d'onda è perfettamente determinata e con essa la quantità di moto, le due grandezze essendo legate dalla relazione di de Broglie λ = h / p. La grandezza fisica correlata la quantità di moto nel principio di indeterminazione è la posizione, che infatti in figura 6 è totalmente indeterminata: l'onda si estende all'infinito. L'altro caso limite è quello di posizione perfettamente determinata, e quantità di moto totalmente indeterminata. I casi intermedi sono descritti da "pacchetti di onde", costituiti dalla sovrapposizione di onde aventi lunghezza d'onda addensate attorno a un valore centrale. Essi sono evocati nella rappresentazione data ai fotoni incidenti in figura 3.
Musica, timbro e modi normali
La Musica è vibrazione e trasmissione di onde sonore che fanno vibrare timpani e anima. La fisica della musica porta a riflettere su concetti di validità più generale. La figura 14 mostra che le vibrazioni di una corda (per esempio di violino) fissata alle estremità sono caratterizzate dalle presenza delle cosiddette “ onde stazionarie ”. Per definizione esse si mantengono invariate nel tempo, facendo astrazione da fenomeni dissipativi. Le onde stazionarie sono “quantizzate”: la lunghezza d’onda λ può assumere solo determinati valori, con la lunghezza l della corda multiplo di ½ λ. Le onde stazionarie corrispondono alle “armoniche” del linguaggio musicale e ai cosiddetti "modi normali" di oscillazione del linguaggio fisico. A ognuno di esse corrisponde una determinata frequenza.
Risuonando, il corpo (cassa armonica in un violino ) di uno strumento musicale amplifica ed esalta in modo diverso le varie armoniche secondo la loro frequenza. La distribuzione in frequenza complessiva è detta “spettro”. Se lo strumento emettesse una sola frequenza sarebbe come un diapason , che serve ma non fa musica. La ricchezza del suono emesso proviene proprio dalla “ sovrapposizione ” delle varie armoniche, ciascuna presente in una certa misura. Il cosiddetto “ timbro ” è determinato dal contenuto spettrale del suono e dalla sua evoluzione nel tempo. Per approfondimenti, vedete Il suono sul testo online La Fisica di Amaldi o il sito Web Fisica Onde Musica , molto completo.
Stati e autostati quantistici
Con le dovute differenze, in Meccanica Quantistica si può ragionare in modo analogo. Il “principio di sovrapposizione” dice che lo stato di una particella o di un sistema può essere rappresentato dalla sovrapposizione delle ampiezze di probabilità corrispondenti a un certo numero di “stati quantistici di base", scelti secondo opportuni criteri e sommati secondo le appropriate regole. La scelta razionale degli quantistici di base cade sui cosiddetti “autostati". Essi sono i corrispondenti quantistici dei modi normali di una corda vibrante, nel senso che in assenza di perturbazioni essi si mantengono nel tempo. Per esempio, gli orbitali elettronici in un atomo sono autostati, definiti da specifici numeri quantici. In questo modo, nell'evoluzione del processo non variano gli autostati ma solo la loro proporzione nella sovrapposizione.
Meccanica Quantistica e fisica classica
In linea di principio, la Meccanica Quantistica ha validità generale e non ristretta al mondo delle particelle elementari. Esperimenti recenti hanno mostrato che il comportamento onda-particella vale anche per molecole, anche grandi. Ma si può andare oltre, almeno in linea di principio. Come si è visto, la lunghezza d'onda è inversamente proporzionale alla quantità di moto: nel mondo macroscopico della fisica classica, masse e quantità di moto sono enormi rispetto a quelle delle particelle. Di conseguenza, le lunghezze d'onda sono talmente piccole da rendere totalmente invisibile ogni effetto quantistico. La Meccanica Quantistica è totalmente compatibile con la fisica classica, che resta una valida approssimazione nella sua " riserva indiana ".
Oggi e domani
La rivoluzione scientifica iniziata con il Novecento impatta molto fortemente sulla nostra vita pratica.
Senza la Relatività, il navigatore non vi aiuterebbe a trovare la buona pizzeria ove volete andare: il funzionamento del GPS richiede che si tenga conto della Relatività, sia Ristretta che Generale. Per esempio, se trascurassimo la Relatività Generale, un GPS che desse la correttamente posizione ad un certo istante, dopo un giorno sbaglierebbe di 10 km.
La Meccanica Quantistica-Ondulatoria ha invaso la nostra vita con le sue applicazioni tecnologiche e gli svariatissimi dispositivi elettronici oggi dilaganti, a cominciare da quella specie di protesi chiamata telefonino. E non avremmo neppure il laser, ormai infilato dappertutto anche all'insaputa di molti (vedete ad esempio Da Alan Turing al calcolo quantistico e Laser e Ottica Quantistica ).
Il progresso prosegue a ritmo rapidissimo. Considerando ad esempio il calcolo, pochi riferimenti bastano a testimoniarlo. La figura 15 mostra la Programma 101 della Olivetti, che fu il primo calcolatore da tavolo programmabile del mondo e fu posto in commercio nel 1965. I nostri attuali calcolatori utilizzano “microprocessori”. Il primo a essere commercializzato fu l’ Intel 4004 , nel 1971. La Apple I uscì nel 1976, approfittando dell'era della microelettronica e con importanti innovazioni comprendenti in primo luogo l'aggiunta di un visore. I microprocessori di oggi includono diversi componenti a un altissimo livello di integrazione, con la presenza di oltre un miliardo di elementi. La figura 16 mostra l' Intel 8742 . E ci sia avvia verso il "calcolo quantistico", del quale tratta Da Alan Turing al calcolo quantistico .
Ragazzi di oggi, mettetevi al passo.
Collegamenti e bibliografia
Peter Atkins e Loretta Jones, Gli atomi: il mondo quantico , La Chimica di Atkins, W.H. Freeman - Zanichelli (2007, testo su Web)
R.P. Feynman, R.B. Leighton e M. Sands, La Fisica di Feynman (The Feynman’s Lectures on Physics), Vol. 3, Cap. 1, Addison Wesley - Zanichelli (1965)
Ringrazio il "nostro amico" Crisostomo Sciacca per vari suggerimenti e per aver così messo ancor più in evidenza il fascino e il mistero di questa Fisica.
.
.
.
Professore Emerito di Fisica Sperimentale
Università di Napoli "Federico II"
Complesso Univ. Monte S. Angelo
Via Cintia - 80126 Napoli - Italy
Onde e particelle per pedoni molto curiosi è stato creato da P. Strolin
Onde e particelle per pedoni molto curiosi
...................................................................
Per domande: autore o
Domanda a un esperto
................Guardate in figura 1 la statua lignea di monaco buddista del periodo Heian (794-1185), ora affidata al Museo Nazionale di Kyoto . L’immagine nasce da una cultura figurativa in cui il valore simbolico ha un ruolo primario. Non è mera rappresentazione di una realtà materiale. E’ magica materializzazione lignea di un’immagine mentale, a sua volta frutto di una visione filosofica. Ci colpisce e attrae con suo sottile e profondo mistero. Vorreste decifrarlo?
Fig. 1. Il monaco Baozhi (Important Cultural Property)
J. Hōshi, Periodo Heian (794-1185), Tempio di Saiō-ji, Kyoto
Clic per statua intera da Museo Nazionale di Kyoto
Il sentir parlare di “ dualismo onda-particella ” ci procura un simile turbamento. Ma il mistero può essere indagato. Resterà un fondamentale mistero, ma si potrà capire come nasce, in cosa consiste e cosa implica. Vedremo che la realtà fisica è molto bella e ben diversa da quanto evoca la parola "dualismo".
Onde e particelle venivano classicamente considerate entità concettualmente separate, in alternativa. Con la fisica moderna emerge piuttosto un quadro “ olistico ”, in cui onda e particella sono inserite in una coerente visione unitaria. È come passare da una rozza differenziazione degli umani tra femmine e maschi a una visione più profonda: in termini degli orientali yin e yang , presenti in diverse proporzioni, ma sempre entro lo stesso ambito umano. Lo rappresenta il ben noto simbolo, con campi bianco e nero racchiusi in un unico cerchio.
Sono richieste conoscenze elementari di Fisica Quantistica, quali quelle esposte in Da linee di Fraunhofer ad atomo quantistico e fornite in modo sistematico in Gli atomi: il mondo quantico nel testo online La Chimica di Atkins.
Scoperta di un nuovo mondo
Il volgere dell'Ottocento e i primi decenni del Novecento segnarono l'inizio di una nuova epoca, nella Scienza come in altri aspetti della cultura umana. Per esempio, nelle arti figurative l' Impressionismo diede il via all'arte moderna e a tutte le sue evoluzioni e rivoluzioni.
Fatti sperimentali “impossibili” (secondo il pensiero vigente in quel tempo) furono elaborati grazie a un’incredibile attività intellettuale e portarono alla "Meccanica Quantistica” (vedete Da linee di Fraunhofer ad atomo quantistico ). Essa si dimostrò di capace di descrivere i fenomeni alla scala atomica, estesa a livelli inferiori grazie a successivi sviluppi. La “Meccanica Classica” resta limitata al mondo macroscopico, ove mantiene la sua validità.
Negli stessi anni fu concepita la “Teoria della Relatività”, una grandiosa costruzione intellettuale partita dal fatto sperimentale che la velocità della luce è una costante, indipendente dal sistema di riferimento. Le equazioni di Maxwell dell'elettromagnetismo classico non hanno più bisogno di nulla per giustificare l'invarianza della velocità della luce (vedete Simmetrie e Relatività Speciale e Interazione Elettromagnetica "alla Feynman" ).
Fig. 2. "Sono stanca di questa forma. Sono curiosa di sapere che cosa succederebbe se fosse rotonda"
Così fu inventata la ruota?
Liza Donnelly , The New Yorker - Immagine Rapporto annuale Pirelli 2012
Con le sue applicazioni, questa rivoluzione scientifica oggi pervade anche il quotidiano e lo farà ancor di più in futuro. E' passato un secolo e almeno i suoi fondamenti dovrebbero far parte di un patrimonio di conoscenza comune.
Qui vedremo i fondamenti della Meccanica Quantistica, in modo concettualmente accessibile a chi non possiede strumenti matematici professionali. Rivivremo le emozioni della Scienza nel collegare e sublimare in sintesi teoriche nuovi fatti sperimentali.
Nel titolo “Onde e particelle per pedoni molto curiosi” è parafrasato quello di uno storico libro di Harry Lipkin sulla "Teoria dei Gruppi" (Lie groups for pedestrians - Gruppi di Lie per pedoni) per persone non dotate di strumenti specifici). Abbiamo aggiunto "molto curiosi". Infatti, è noto da tempi immemorabili che la curiosità è un motore di conoscenza e di progresso (figura 2).
Nuovi fatti sperimentali
Le nuove teorie si basano su nuovi fatti sperimentali e/o acute interpretazioni di dati esistenti. I nuovi fatti sperimentali che si presentarono erano molto intriganti per non dire sconvolgenti. Per massima concisione citiamone due, fondamentali. Sperimentalmente si vide che le onde elettromagnetiche, quale è la luce, si possono comportare anche come particelle: nel cosiddetto "effetto fotoelettrico", esse agiscono come "quanti" cioè come particelle. D'altra parte, fu osservata la "diffrazione di elettroni" da parte di fenditure: le particelle manifestano fenomeni di interferenza tipici delle onde.
Effetto fotoelettrico: onde come particelle
Vediamo anzitutto l’ effetto fotoelettrico e la sua interpretazione quantistica, che segnarono l'inizio di una nuova visione della Fisica portando a frutto un aspetto del progresso scientifico su largo campo iniziato quasi un secolo prima con l'osservazione delle cosiddette "Linee di Fraunhofer" (vedete Da linee di Fraunhofer a Universo in-espansione e Da linee di Fraunhofer ad atomo quantistico ).
Una radiazione elettro-magnetica può essere trasmessa agli elettroni in un atomo e estrarli dall’atomo stesso. La teoria ondulatoria della radiazione elettro-magnetica, formulata da Maxwell poco dopo metà Ottocento, fa prevedere che riducendo l’intensità della radiazione si possa giungere al punto in cui essa non apporti più energia sufficiente per estrarre gli elettroni. Non è così. Il fenomeno si attenua ma persiste. Non dipende dall'intensità ma piuttosto dalla "frequenza" della radiazione.
L'interpretazione data da Albert Einstein nel 1905 fu che l’energia arriva a pacchetti, detti “quanti” (figura 3). Questo comportamento è tipico delle particelle. Diminuendo l’intensità della radiazione, si riduce solamente il flusso di quanti. L'energia E di ogni singolo quanto dipende unicamente dalla frequenza f della radiazione. Anzi è praticamente la stessa cosa. Essa è, infatti, data dalla frequenza moltiplicata per una costante h : E = h f.
La costante h era stata introdotta da Max Planck nel 1900 per spiegare la distribuzione dell'energia (spettro) trasmessa alla materia da una radiazione attraverso una "quantizzazione" dell'energia stessa, ossia l'assunzione di valori variabili "a scalino" invece che in modo continuo. Con l'interpretazione di Einstein dell'effetto fotoelettrico, essa viene associata non solo a uno scalino ma anche a un "quanto" di energia con le caratteristiche di una particella. L'innovazione concettuale èi fondamentale.
La "costante di Planck" h irrompe così prepotentemente nel mondo della Fisica, caratterizzandola al livello quantistico-ondulatorio. Si entra in un dominio di nuova Scienza. Essa ha un valore molto piccolo: h = 1,2 x 10 -13 (GeV/c) cm. I fenomeni ad essa connessi non sono quindi generalmente visibili per corpi a una scala macroscopica.
| ..........................
Fig. 3. Effetto fotoelettrico nella visione quantistica Immagine Scienza e Musica | ... | ......................
Fig. 4. Diffrazione di elettroni da un reticolo cristallino per interferenza costruttiva - Immagine Physics Alerts |
Sviluppi del pensiero scientifico, a volo d'uccello
Da linee di Fraunhofer ad atomo quantistico narra che l'aurora della comprensione della natura ondulatoria dell'elettrone, archetipo di particella elementare, venne nel 1913 con il "Modello atomico di Bohr", nel quale i livelli energetici discreti (non con valori continui) osservati per l'atomo di Idrogeno sono interpretati come effetto di una provvidenziale quantizzazione del momento angolare. L' ipotesi di una natura ondulatoria dell'elettrone sorse infine nel 1924 per opera di Louis de Broglie. Divenne così possibile associare la quantizzazione del momento angolare a orbite degli elettroni vincolate a corrispondere a " onde stazionarie ".
il " principio di indeterminazione " (1927) impose di accettare l'impossibilità di determinare contemporaneamente con qualsivoglia precisione due grandezze fisiche che nel mondo quantistico sono "correlate", quali sono la posizione e la quantità di moto di una particella o il tempo in cui è osservata e la sua energia.
Più precisamente, il prodotto delle loro indeterminazioni resta costante e il suo valore è dato dalla costante di Planck, che si si riafferma come la costante fondamentale della Fisica Quantistica: se agiamo per diminuire l'una, l'altra scappa automaticamente in su.
Accade anche nel gioco mostrato in figura 5 con una fotografia del grande captatore di istanti umani Robert Doisneau .
Fig. 5. La mariée chez Gégene (La sposa da Gégene), 1946
Robert Doisneau - Immagine Atelier Robert Doisneau
L' Equazione di Schrödinger (1926) unì natura ondulatoria e Principio di Indeterminazione sotto lo stesso tetto della costante di Planck, per descrivere il comportamento dell'elettrone. Al concetto di orbita definita e fissa del modello atomico di Bohr si sostituì quello di " orbitale ", caratterizzato da una distribuzione di probabilità.
Infine l' Equazione di Dirac - concepita nel 1927 per essere valida anche in regime relativistico - sorprendentemente incluse lo " spin " dell'elettrone e permise di tenerne conto nella descrizione degli orbitali elettronici.
L'Equazione di Dirac aprì la strada alla fisica delle particelle elementari. Essa sorprese anche con la predizione dell'esistenza di " anti-particelle ", che tuttora produce uno sconcerto acquietato solamente approfondendone la conoscenza negli aspetti teorici e sperimentali. La predizione fu confermata dalla scoperta dell'anti-elettrone ("positrone") nel 1932.
Diffrazione di elettroni: particelle come onde
In fisica classica, i fenomeni di interferenza sono caratteristici della onde e gli esperimenti su fenditure costituiscono una efficace metodologia sperimentale per osservarli. Così il celebre esperimento di Young (1803) mise in evidenza il carattere ondulatorio della luce attraverso l'osservazione di una sua diffrazione come effetto di un fenomeno di interferenza.
L' osservazione sperimentale diretta della natura ondulatoria dell'elettrone fu fornita negli anni 1925-27 da Clinton Davisson e Lester Germer nonché indipendentemente da George Paget Thomson, che ne osservarono la diffrazione su un reticolo cristallino. La figura 4 mostra che si ha un picco di interferenza costruttiva per certi angoli (50 o in figura) dipendenti dal rapporto tra la lunghezza d'onda dell'elettrone λ indicata dall' ipotesi ondulatoria di de Broglie e la distanza d tra gli atomi del reticolo, secondo una legge corrispondente alla " relazione di Bragg " della fisica classica. In figura non è mostrato il contributo all'interferenza costruttiva dato dagli strati immediatamente sottostanti del reticolo. George Thomson osservò un simile effetto diffrattivo all’attraversamento di una sottile lamina d’oro.
Onde: ampiezza e intensità
La figura 6 mostra la "ampiezza" e la "intensità" della oscillazione provocata da un'onda generica, in un dato punto dello spazio e in funzione del tempo. Per vederne il significato nella pratica, vi propongo di "pensare" a una breve uscita in mare. Il mare monta, l’altezza (che possiamo anche dire ampiezza) delle onde raddoppia, senza che per fortuna l’onda si rompa. Il timore quadruplica in intensità, perché è collegato alla grandezza fisica che caratterizza l'impatto dell'onda: l’energia trasportata dal moto ondoso. In generale, una trattazione matematica completa porta a concludere che l'intensità (sempre positiva) di un'onda è proporzionale al quadrato della sua ampiezza (oscillante). L'andar per mare può aiutare a capire la Fisica.
| ............................................................................................................
Fig. 6. Ampiezza e intensità di un'onda Immagine School Physics | ..... | ...............................................................................
Fig. 7. Un esperimento pensato sulla conservazione della quantità di moto Arbor Scientific (2013) - Immagine Arbor Scientific |
La doppia fenditura in esperimenti pensati
Dal punto di vista del meccanismo di formazione dell'interferenza, l'apparato di Young, il reticolo cristallino di Davisson e Germer e gli atomi nella sottile lamina d’oro di Thomson sono concettualmente equivalenti a un apparato ideale detto "doppia fenditura", implicitamente assunto di scala dimensionale atta a evidenziare fenomeni diffrattivi .
In quel capolavoro di divulgazione scientifica che è il Dialogo sopra i due massimi sistemi del mondo (pubblicato nel 1632), Galileo Galilei espone il suo concetto di relatività facendo pensare il lettore a un "navilio" all’interno del quale delle farfalle volano senza accorgersi del suo moto relativamente al mondo circostante. Potete trarre piacere dalla lettura di una trascrizione parziale del bellissimo testo di Galileo su Simmetrie e Relatività Speciale .
Il navilio di Galileo è uno storico esempio di “ esperimento pensato ” (noto con la denominazione tedesca "gedanken experiment"). Un esperimento pensato, non necessariamente realistico ma aderente alla sostanza del fenomeno, può costituire un efficace strumento per capire e far capire. Con perfida ironia, la figura 7 ne fornisce un esempio.
Le figure 8 e 9 sono tratte dalla preziosa Fisica di Feynman e rappresentano esperimenti pensati semplici e incisivi, metodologicamente basati sul concetto di esperimento con doppia fenditura applicato a onde e particelle. Seguiremo la traccia data da Richard Feynman . Vale la pena non sottrarsi al fascino della sua personalità e ascoltarne una viva lezione sull'argomento qui trattato, disponibile sul Web. Se vi capita, leggete i libri di divulgazione scientifica e qualsiasi cosa egli abbia scritto, non solo su argomenti di Fisica. Quello che accade con onde e particelle può essere visto anche in una animazione visibile sul Web, o in una fantasiosa lezione del Dr. Quantum . In italiano, sono disponibili le diapositive di un seminario "fatto in casa" e collegato a questo sito Web.
Fig. 8. Onde su fenditure (da La Fisica di Feynman)
Onde elettromagnetiche su doppia fenditura
La figura 8 illustra schematicamente cosa accade quando delle onde (per ora di qualsiasi natura) investono una doppia (1 e 2) fenditura caratterizzata da una scala dimensionale a distanza paragonabile alla lunghezza d'onda. Su un piano di osservazione (absorber) oltre le fenditure, l'intensità I 12 del segnale con ambedue le fenditure aperte mostra le frange d'interferenza tipiche delle onde (c in figura
Focalizziamo l'attenzione sulle onde elettromagnetiche (vedete Interazione Elettromagnetica "alla Feynman" ) e domandiamoci se questo comportamento persista quando l'intensità della sorgente è ridotta indefinitamente. A un certo punto si inizia a vedere che il segnale non è continuo. Esso arriva a colpi, sotto forma di singoli punti luminosi sul piano di osservazione se questo è uno schermo con la proprietà di emettere luce quando colpito. Si osservano singoli "quanti". I quanti osservati sono della stessa natura di quelli che provocano l'effetto fotoelettrico. Come nell'effetto fotoelettrico, la fisica classica è superata: le onde elettromagnetiche sono anche particelle, chiamate " fotoni ".
Incuriositi, continuiamo ad accumulare punti luminosi sullo schermo. Quello che accade diventa proprio incredibile. I quanti arrivano a colpi come particelle e in base alla loro concezione classica ci attenderemmo che essi attraversino l'una o l'altra fenditura, fornendo un segnale complessivo uguale a I 1 + I 2 . Non è così. I singoli quanti si distribuiscono automaticamente uno dopo l'altro in bande separate da zone vuote, e l'immagine che si va costruendo assomiglia sempre più alla classica figura di interferenza I 12 osservata per le onde. I singoli quanti mantengono anche un comportamento da onda. E' come se un singolo quanto attraversasse “ambedue” le fenditure al pari di un'onda, interferendo con sé stesso in modo che colpo dopo colpo si formino le classiche frange d'interferenza.
In sintesi, le onde elettromagnetiche sono costituite da quanti, che arrivano a colpi come particelle ma danno luogo a interferenza come onde. Per dirla come Massimo Troisi in Pensavo fosse amore... invece era un calesse , ma con ritorno di fiamma: pensavamo che fossero onde e sono particelle, e queste si comportano anche da onda. Di primo acchito possono sembrare giochi di parole e confondere. In realtà rappresentano l'integrazione dei concetti di onda e particella in un unico cerchio alla yin e yang della quale si è parlato inizialmente, abitualmente chiamata dualismo anche se questa denominazione può non contribuire alla chiarezza.
Questo per quanto riguarda il fotone, nato da un'onda come la Venere del Botticelli . Curiosità impone.di vedere come l'elettrone, nato come particella "alla Democrito ", si comporta con una doppia fenditura. Troveremo simmetria?
Fig. 9. Elettroni su fenditure (da La Fisica di Feynman)
Elettroni su doppia fenditura
Rivolgiamo ora l'attenzione sulla figura 9, dove consideriamo che la doppia fenditura sia investita da particelle con credenziali doc: elettroni. Partendo da una configurazione nella quale essi si comportano da particelle, “immaginiamo" di diminuire progressivamente le fenditure in larghezza e distanza.
Abbiamo una grossa sorpresa: a un certo punto appaiono frange d’interferenza come mostrato in (c), in modo puramente indicativo. Dalla distanza tra le frange si può anche dedurre una lunghezza d’onda λ associata agli elettroni e scoprire che essa è legata all'inverso della loro quantità di moto p da una costante moltiplicativa, di nuovo la costante h di Planck: λ = h / p come nell' ipotesi ondulatoria di de Broglie. È come se lo stesso elettrone passasse attraverso ambedue le fenditure. La figura 10 mostra quanto questo sia paradossale nella visione classica: se il treno avesse un comportamento quantistico, dovrebbe tranquillamente poter passare attraverso ambedue i tunnel.
| ...........................................
Fig. 10. Se un treno si comportasse come un elettrone Immagine The Mysearch Website | ..... | ..................................
Fig. 11. Animazione con elettroni (o singoli fotoni) su doppia fenditura Immagine Wikipedia |
Abbiamo detto “immaginiamo” e abbiamo così approfittato dei vantaggi degli esperimenti pensati. Continuando con l'immaginazione, registriamo uno a uno l'impatto dei singoli elettroni. Come i singoli fotoni di cui sopra, vediamo gli elettroni accumularsi formando man mano frange di interferenza. Lo mostra l'animazione in figura 11, che potrebbe anche essere riferita al comportamento di singoli fotoni precedentemente descritto. Vi è simmetria tra elettroni e fotoni. Per entrambi le due rappresentazioni possono concettualmente coesistere: essi sono onde "e" particelle. La fisica classica è superata: in essa l'essere onda "oppure" particella sono mutualmente esclusivi.
È difficilissimo passare da un esperimento pensato a uno reale, con registrazione di elettroni singoli. Le fenditure devono avere dimensioni e distanze straordinariamente piccole: la grandezza di riferimento è la lunghezza d'onda di de Broglie dell'elettrone, la quale risente del piccolissimo valore della costante di Planck. Ma nel 1976 con raffinatissimi accorgimenti l’esperimento fu realmente eseguito all’Università di Bologna e fu vista l' interferenza quantistica di singoli elettroni .
Indeterminazione e probabilità: Oh Alice ... Ma Bob...
Le sorprese si aggiungono alle sorprese. Immaginiamo di riuscire, in qualche modo, a determinare da quale delle due fenditure l'elettrone sia passato: l'interferenza scompare. Se osservato, l’elettrone fa come i bambini e si comporta da "brava particella". In termini scientifici, il suo comportamento da onda è collegato alla "indeterminazione" nella fenditura dalla quale è passato. È una manifestazione del principio di indeterminazione, del quale abbiamo già parlato, Possiamo solo assegnare una "probabilità" al passaggio attraverso ciascuna delle fenditure. Due nuove parole entrano nella rigorosa Fisica al livello fondamentale: "indeterminazione" e "probabilità". Con esse, la costante h di Planck ha colpito ancora. Le certezze e realtà assolute ottocentesche - con i loro risvolti di arroganza da parte delle piccole menti - sono ora sanamente mutate in realtà probabilistiche, come in altri campi del sapere, nella vita personale e nell'evoluzione di sistemi complessi quale è per esempio la società umana: la Fisica si è umanizzata.
I paradossi fanno capire la portata rivoluzionaria di nuove visioni della Scienza, non solo in quanto qui discusso (vedete per esempio Simmetrie e Relatività Speciale ). L'ironia usa spesso lo stesso strumento, come mostra la figura 12.
Fig. 12. Oh Alice ... tu sei la sola per me
Ma Bob ... in un mondo quantistico come puoi esserne sicuro?
Immagine Physics Intuition Applications
Fisica Quantistica: probabilità
Dice Feynman nelle sue lezioni già citate parlando degli esperimenti descritti sopra, concettualmente chiamati "su doppia fenditura":
“We choose to examine a phenomenon which is impossible, absolutely impossible, to explain in any classical way, and which has in it the heart of Quantum Mechanics. In reality, it contains the only mystery"
(Scegliamo di esaminare un fenomeno che è impossibile, assolutamente impossibile , spiegare in alcun modo classico, e che ha in sé il cuore della Meccanica Quantistica. In realtà, esso contiene l'unico mistero).
(Scegliamo di esaminare un fenomeno che è impossibile, assolutamente impossibile , spiegare in alcun modo classico, e che ha in sé il cuore della Meccanica Quantistica. In realtà, esso contiene l'unico mistero).
Questa sorprendente rivoluzione concettuale pose la sfida scientifica di inquadrarla in una struttura matematica coerente. Come prima cosa, che fare ora che il principio di indeterminazione ci impedisce di dire che una particella "ha" certe coordinate spaziali e una certa quantità di moto? Dobbiamo trattarla come un'onda "e" in termini probabilistici. La figura 6 viene in soccorso, dando la "dritta". In primo luogo, la probabilità deve essere sempre positiva: non può che corrispondere a quella che in fisica classica è l'intensità dell'onda, precedentemente definita come il quadrato dell'ampiezza. Sempre iniziando con un riferimento alla fisica classica, i meccanismi dei fenomeni sono descritti ragionando sull'ampiezza: come potrebbero altrimenti le intensità (sempre positive) di due onde sommarsi algebricamente e dar luogo non solo a interferenza costruttiva, ma anche distruttiva?
Fisica Quantistica: ampiezza di probabilità
Da quanto detto sopra si può capire che anche in Fisica Quantistica per la descrizione dei fenomeni si deve ragionare sull'ampiezza. Essa assume il nome di "ampiezza di probabilità" per caratterizzarne la connessione con una probabilità, data da un'operazione che nell'appropriato formalismo matematico corrisponde a un'elevazione a potenza al quadrato, proprio come per le onde in figura 6.
Si è precedentemente detto che il comportamento di una particella come l'elettrone è descritto dall'Equazione di Schrödinger o, in maniera più completa, dall'equazione di Dirac, Va da sè che esse operano su "ampiezze di probabilità". Le loro soluzioni sono dette " funzioni d'onda ". Lo sono gli orbitali che descrivono lo stato di un elettrone in un atomo in corrispondenza di specifici "numeri quantici" (vedete Da linee di Fraunhofer ad atomo quantistico ). Un esempio di orbitale è dato in figura 13, che mostra la distribuzione di probabilità sotto forma di "nube elettronica".
| ....................................................................
Fig. 13. La nube elettronica dell’orbitale
1s dell’atomo di Idrogeno Immagine La Chimica di Atkins - Zanichelli | ....... | .......................................
Fig. 14. Gli stati stazionari delle corde vibranti Immagine Univ. Wisconsin Platteville |
Riflettendo, un orbitale non rappresenta un elettrone singolo, ma piuttosto l'elettrone nel "sistema atomo", con funzione d'onda determinata dal legame con il nucleo. Che dire di una particella libera, elettrone, fotone o altra che sia? La figura 6 viene di nuovo in soccorso. L'onda che mostra può essere vista come rappresentazione di un caso limite contemplato dal principio di indeterminazione, ove la costante di Planck fissa il prodotto delle indeterminazioni di variabili correlate. Nella figura, la lunghezza d'onda è perfettamente determinata e con essa la quantità di moto, le due grandezze essendo legate dalla relazione di de Broglie λ = h / p. La grandezza fisica correlata la quantità di moto nel principio di indeterminazione è la posizione, che infatti in figura 6 è totalmente indeterminata: l'onda si estende all'infinito. L'altro caso limite è quello di posizione perfettamente determinata, e quantità di moto totalmente indeterminata. I casi intermedi sono descritti da "pacchetti di onde", costituiti dalla sovrapposizione di onde aventi lunghezza d'onda addensate attorno a un valore centrale. Essi sono evocati nella rappresentazione data ai fotoni incidenti in figura 3.
Musica, timbro e modi normali
La Musica è vibrazione e trasmissione di onde sonore che fanno vibrare timpani e anima. La fisica della musica porta a riflettere su concetti di validità più generale. La figura 14 mostra che le vibrazioni di una corda (per esempio di violino) fissata alle estremità sono caratterizzate dalle presenza delle cosiddette “ onde stazionarie ”. Per definizione esse si mantengono invariate nel tempo, facendo astrazione da fenomeni dissipativi. Le onde stazionarie sono “quantizzate”: la lunghezza d’onda λ può assumere solo determinati valori, con la lunghezza l della corda multiplo di ½ λ. Le onde stazionarie corrispondono alle “armoniche” del linguaggio musicale e ai cosiddetti "modi normali" di oscillazione del linguaggio fisico. A ognuno di esse corrisponde una determinata frequenza.
Risuonando, il corpo (cassa armonica in un violino ) di uno strumento musicale amplifica ed esalta in modo diverso le varie armoniche secondo la loro frequenza. La distribuzione in frequenza complessiva è detta “spettro”. Se lo strumento emettesse una sola frequenza sarebbe come un diapason , che serve ma non fa musica. La ricchezza del suono emesso proviene proprio dalla “ sovrapposizione ” delle varie armoniche, ciascuna presente in una certa misura. Il cosiddetto “ timbro ” è determinato dal contenuto spettrale del suono e dalla sua evoluzione nel tempo. Per approfondimenti, vedete Il suono sul testo online La Fisica di Amaldi o il sito Web Fisica Onde Musica , molto completo.
Stati e autostati quantistici
Con le dovute differenze, in Meccanica Quantistica si può ragionare in modo analogo. Il “principio di sovrapposizione” dice che lo stato di una particella o di un sistema può essere rappresentato dalla sovrapposizione delle ampiezze di probabilità corrispondenti a un certo numero di “stati quantistici di base", scelti secondo opportuni criteri e sommati secondo le appropriate regole. La scelta razionale degli quantistici di base cade sui cosiddetti “autostati". Essi sono i corrispondenti quantistici dei modi normali di una corda vibrante, nel senso che in assenza di perturbazioni essi si mantengono nel tempo. Per esempio, gli orbitali elettronici in un atomo sono autostati, definiti da specifici numeri quantici. In questo modo, nell'evoluzione del processo non variano gli autostati ma solo la loro proporzione nella sovrapposizione.
Meccanica Quantistica e fisica classica
In linea di principio, la Meccanica Quantistica ha validità generale e non ristretta al mondo delle particelle elementari. Esperimenti recenti hanno mostrato che il comportamento onda-particella vale anche per molecole, anche grandi. Ma si può andare oltre, almeno in linea di principio. Come si è visto, la lunghezza d'onda è inversamente proporzionale alla quantità di moto: nel mondo macroscopico della fisica classica, masse e quantità di moto sono enormi rispetto a quelle delle particelle. Di conseguenza, le lunghezze d'onda sono talmente piccole da rendere totalmente invisibile ogni effetto quantistico. La Meccanica Quantistica è totalmente compatibile con la fisica classica, che resta una valida approssimazione nella sua " riserva indiana ".
Oggi e domani
La rivoluzione scientifica iniziata con il Novecento impatta molto fortemente sulla nostra vita pratica.
Senza la Relatività, il navigatore non vi aiuterebbe a trovare la buona pizzeria ove volete andare: il funzionamento del GPS richiede che si tenga conto della Relatività, sia Ristretta che Generale. Per esempio, se trascurassimo la Relatività Generale, un GPS che desse la correttamente posizione ad un certo istante, dopo un giorno sbaglierebbe di 10 km.
La Meccanica Quantistica-Ondulatoria ha invaso la nostra vita con le sue applicazioni tecnologiche e gli svariatissimi dispositivi elettronici oggi dilaganti, a cominciare da quella specie di protesi chiamata telefonino. E non avremmo neppure il laser, ormai infilato dappertutto anche all'insaputa di molti (vedete ad esempio Da Alan Turing al calcolo quantistico e Laser e Ottica Quantistica ).
| .......................................... Fig. 15. La Programma 101 della Olivetti Immagine Museo Nazionale della Scienza e della Tecnologia L. da Vinci | ..... | ..............................................
Fig. 16. Il microprocessore Intel 8742 Immagine Wikiwand |
Il progresso prosegue a ritmo rapidissimo. Considerando ad esempio il calcolo, pochi riferimenti bastano a testimoniarlo. La figura 15 mostra la Programma 101 della Olivetti, che fu il primo calcolatore da tavolo programmabile del mondo e fu posto in commercio nel 1965. I nostri attuali calcolatori utilizzano “microprocessori”. Il primo a essere commercializzato fu l’ Intel 4004 , nel 1971. La Apple I uscì nel 1976, approfittando dell'era della microelettronica e con importanti innovazioni comprendenti in primo luogo l'aggiunta di un visore. I microprocessori di oggi includono diversi componenti a un altissimo livello di integrazione, con la presenza di oltre un miliardo di elementi. La figura 16 mostra l' Intel 8742 . E ci sia avvia verso il "calcolo quantistico", del quale tratta Da Alan Turing al calcolo quantistico .
Ragazzi di oggi, mettetevi al passo.
Collegamenti e bibliografia
Peter Atkins e Loretta Jones, Gli atomi: il mondo quantico , La Chimica di Atkins, W.H. Freeman - Zanichelli (2007, testo su Web)
R.P. Feynman, R.B. Leighton e M. Sands, La Fisica di Feynman (The Feynman’s Lectures on Physics), Vol. 3, Cap. 1, Addison Wesley - Zanichelli (1965)
Ringrazio il "nostro amico" Crisostomo Sciacca per vari suggerimenti e per aver così messo ancor più in evidenza il fascino e il mistero di questa Fisica.
Paolo Strolin
.
.
.
Professore Emerito di Fisica Sperimentale
Università di Napoli "Federico II"
Complesso Univ. Monte S. Angelo
Via Cintia - 80126 Napoli - Italy
Ultima Modifica 5 Anni 2 Mesi fa da Paolo.
Si prega Accesso a partecipare alla conversazione.
5 Anni 2 Mesi fa - 5 Anni 2 Mesi fa #182
da Paolo
Risposta da Paolo al topic Onde e particelle per pedoni molto curiosi
P. Strolin ha scritto:
Onde e particelle per pedoni molto curiosi................
...................................................Per domande: autore o Domanda a un esperto................
Guardate in figura 1 la statua lignea di monaco buddista del periodo Heian (794-1185), ora affidata al Museo Nazionale di Kyoto . L’immagine nasce da una cultura figurativa in cui il valore simbolico ha un ruolo primario. Non è mera rappresentazione di una realtà materiale. E’ magica materializzazione lignea di un’immagine mentale, a sua volta frutto di una visione filosofica. Ci colpisce e attrae con suo sottile e profondo mistero. Vorreste decifrarlo?
Fig. 1. Il monaco Baozhi (Important Cultural Property)
J. Hōshi, Periodo Heian (794-1185), Tempio di Saiō-ji, Kyoto
Clic per statua intera da Museo Nazionale di Kyoto
Il sentir parlare di “ dualismo onda-particella ” ci procura un simile turbamento. Ma il mistero può essere indagato. Resterà un fondamentale mistero, ma si potrà capire come nasce, in cosa consiste e cosa implica. Vedremo che la realtà fisica è molto bella e ben diversa da quanto evoca la parola "dualismo".
Onde e particelle venivano classicamente considerate entità concettualmente separate, in alternativa. Con la fisica moderna emerge piuttosto un quadro “ olistico ”, in cui onda e particella sono inserite in una coerente visione unitaria. È come passare da una rozza differenziazione degli umani tra femmine e maschi a una visione più profonda: in termini degli orientali yin e yang , presenti in diverse proporzioni, ma sempre entro lo stesso ambito umano. Lo rappresenta il ben noto simbolo, con campi bianco e nero racchiusi in un unico cerchio.
Sono richieste conoscenze elementari di Fisica Quantistica, quali quelle esposte in Da linee di Fraunhofer ad atomo quantistico e fornite in modo sistematico in Gli atomi: il mondo quantico nel testo online La Chimica di Atkins.
Scoperta di un nuovo mondo
Il volgere dell'Ottocento e i primi decenni del Novecento segnarono l'inizio di una nuova epoca, nella Scienza come in altri aspetti della cultura umana. Per esempio, nelle arti figurative l' Impressionismo diede il via all'arte moderna e a tutte le sue evoluzioni e rivoluzioni.
Fatti sperimentali “impossibili” (secondo il pensiero vigente in quel tempo) furono elaborati grazie a un’incredibile attività intellettuale e portarono alla "Meccanica Quantistica” (vedete Da linee di Fraunhofer ad atomo quantistico ). Essa si dimostrò di capace di descrivere i fenomeni alla scala atomica, estesa a livelli inferiori grazie a successivi sviluppi. La “Meccanica Classica” resta limitata al mondo macroscopico, ove mantiene la sua validità.
Negli stessi anni fu concepita la “Teoria della Relatività”, una grandiosa costruzione intellettuale partita dal fatto sperimentale che la velocità della luce è una costante, indipendente dal sistema di riferimento. Le equazioni di Maxwell dell'elettromagnetismo classico non hanno più bisogno di nulla per giustificare l'invarianza della velocità della luce (vedete Simmetrie e Relatività Speciale e Interazione Elettromagnetica "alla Feynman" ).
Fig. 2. "Sono stanca di questa forma. Sono curiosa di sapere che cosa succederebbe se fosse rotonda"
Così fu inventata la ruota?
Liza Donnelly , The New Yorker - Immagine Rapporto annuale Pirelli 2012
Con le sue applicazioni, questa rivoluzione scientifica oggi pervade anche il quotidiano e lo farà ancor di più in futuro. E' passato un secolo e almeno i suoi fondamenti dovrebbero far parte di un patrimonio di conoscenza comune.
Qui vedremo i fondamenti della Meccanica Quantistica, in modo concettualmente accessibile a chi non possiede strumenti matematici professionali. Rivivremo le emozioni della Scienza nel collegare e sublimare in sintesi teoriche nuovi fatti sperimentali.
Nel titolo “Onde e particelle per pedoni molto curiosi” è parafrasato quello di uno storico libro di Harry Lipkin sulla "Teoria dei Gruppi" (Lie groups for pedestrians - Gruppi di Lie per pedoni) per persone non dotate di strumenti specifici). Abbiamo aggiunto "molto curiosi". Infatti, è noto da tempi immemorabili che la curiosità è un motore di conoscenza e di progresso (figura 2).
Nuovi fatti sperimentali
Le nuove teorie si basano su nuovi fatti sperimentali e/o acute interpretazioni di dati esistenti. I nuovi fatti sperimentali che si presentarono erano molto intriganti per non dire sconvolgenti. Per massima concisione citiamone due, fondamentali. Sperimentalmente si vide che le onde elettromagnetiche, quale è la luce, si possono comportare anche come particelle: nel cosiddetto "effetto fotoelettrico", esse agiscono come "quanti" cioè come particelle. D'altra parte, fu osservata la "diffrazione di elettroni" da parte di fenditure: le particelle manifestano fenomeni di interferenza tipici delle onde.
Effetto fotoelettrico: onde come particelle
Vediamo anzitutto l’ effetto fotoelettrico e la sua interpretazione quantistica, che segnarono l'inizio di una nuova visione della Fisica portando a frutto un aspetto del progresso scientifico su largo campo iniziato quasi un secolo prima con l'osservazione delle cosiddette "Linee di Fraunhofer" (vedete Da linee di Fraunhofer a Universo in-espansione e Da linee di Fraunhofer ad atomo quantistico ).
Una radiazione elettro-magnetica può essere trasmessa agli elettroni in un atomo e estrarli dall’atomo stesso. La teoria ondulatoria della radiazione elettro-magnetica, formulata da Maxwell poco dopo metà Ottocento, fa prevedere che riducendo l’intensità della radiazione si possa giungere al punto in cui essa non apporti più energia sufficiente per estrarre gli elettroni. Non è così. Il fenomeno si attenua ma persiste. Non dipende dall'intensità ma piuttosto dalla "frequenza" della radiazione.
L'interpretazione data da Albert Einstein nel 1905 fu che l’energia arriva a pacchetti, detti “quanti” (figura 3). Questo comportamento è tipico delle particelle. Diminuendo l’intensità della radiazione, si riduce solamente il flusso di quanti. L'energia E di ogni singolo quanto dipende unicamente dalla frequenza f della radiazione. Anzi è praticamente la stessa cosa. Essa è, infatti, data dalla frequenza moltiplicata per una costante h : E = h f.
La costante h era stata introdotta da Max Planck nel 1900 per spiegare la distribuzione dell'energia (spettro) trasmessa alla materia da una radiazione attraverso una "quantizzazione" dell'energia stessa, ossia l'assunzione di valori variabili "a scalino" invece che in modo continuo. Con l'interpretazione di Einstein dell'effetto fotoelettrico, essa viene associata non solo a uno scalino ma anche a un "quanto" di energia con le caratteristiche di una particella. L'innovazione concettuale èi fondamentale.
La "costante di Planck" h irrompe così prepotentemente nel mondo della Fisica, caratterizzandola al livello quantistico-ondulatorio. Si entra in un dominio di nuova Scienza. Essa ha un valore molto piccolo: h = 1,2 x 10 -13 (GeV/c) cm. I fenomeni ad essa connessi non sono quindi generalmente visibili per corpi a una scala macroscopica.
..........................
Fig. 3. Effetto fotoelettrico nella visione quantistica
Immagine Scienza e Musica
... ......................
Fig. 4. Diffrazione di elettroni da un reticolo cristallino
per interferenza costruttiva - Immagine Physics Alerts
Sviluppi del pensiero scientifico, a volo d'uccello
Da linee di Fraunhofer ad atomo quantistico narra che l'aurora della comprensione della natura ondulatoria dell'elettrone, archetipo di particella elementare, venne nel 1913 con il "Modello atomico di Bohr", nel quale i livelli energetici discreti (non con valori continui) osservati per l'atomo di Idrogeno sono interpretati come effetto di una provvidenziale quantizzazione del momento angolare. L' ipotesi di una natura ondulatoria dell'elettrone sorse infine nel 1924 per opera di Louis de Broglie. Divenne così possibile associare la quantizzazione del momento angolare a orbite degli elettroni vincolate a corrispondere a " onde stazionarie ".
il " principio di indeterminazione " (1927) impose di accettare l'impossibilità di determinare contemporaneamente con qualsivoglia precisione due grandezze fisiche che nel mondo quantistico sono "correlate", quali sono la posizione e la quantità di moto di una particella o il tempo in cui è osservata e la sua energia.
Più precisamente, il prodotto delle loro indeterminazioni resta costante e il suo valore è dato dalla costante di Planck, che si si riafferma come la costante fondamentale della Fisica Quantistica: se agiamo per diminuire l'una, l'altra scappa automaticamente in su.
Accade anche nel gioco mostrato in figura 5 con una fotografia del grande captatore di istanti umani Robert Doisneau .
Fig. 5. La mariée chez Gégene (La sposa da Gégene), 1946
Robert Doisneau - Immagine Atelier Robert Doisneau
L' Equazione di Schrödinger (1926) unì natura ondulatoria e Principio di Indeterminazione sotto lo stesso tetto della costante di Planck, per descrivere il comportamento dell'elettrone. Al concetto di orbita definita e fissa del modello atomico di Bohr si sostituì quello di " orbitale ", caratterizzato da una distribuzione di probabilità.
Infine l' Equazione di Dirac - concepita nel 1927 per essere valida anche in regime relativistico - sorprendentemente incluse lo " spin " dell'elettrone e permise di tenerne conto nella descrizione degli orbitali elettronici.
L'Equazione di Dirac aprì la strada alla fisica delle particelle elementari. Essa sorprese anche con la predizione dell'esistenza di " anti-particelle ", che tuttora produce uno sconcerto acquietato solamente approfondendone la conoscenza negli aspetti teorici e sperimentali. La predizione fu confermata dalla scoperta dell'anti-elettrone ("positrone") nel 1932.
Diffrazione di elettroni: particelle come onde
In fisica classica, i fenomeni di interferenza sono caratteristici della onde e gli esperimenti su fenditure costituiscono una efficace metodologia sperimentale per osservarli. Così il celebre esperimento di Young (1803) mise in evidenza il carattere ondulatorio della luce attraverso l'osservazione di una sua diffrazione come effetto di un fenomeno di interferenza.
L' osservazione sperimentale diretta della natura ondulatoria dell'elettrone fu fornita negli anni 1925-27 da Clinton Davisson e Lester Germer nonché indipendentemente da George Paget Thomson, che ne osservarono la diffrazione da parte di un reticolo cristallino. La figura 4 mostra che si ha un picco di interferenza costruttiva per certi angoli (50 o in figura) dipendenti dal rapporto tra la lunghezza d'onda dell'elettrone λ indicata dall' ipotesi ondulatoria di de Broglie e la distanza d tra gli atomi del reticolo, secondo una legge corrispondente alla " relazione di Bragg " della fisica classica. In figura non è mostrato il contributo all'interferenza costruttiva dato dagli strati immediatamente sottostanti del reticolo. George Thomson osservò un simile effetto diffrattivo all’attraversamento di una sottile lamina d’oro.
Onde: ampiezza e intensità
La figura 6 mostra la "ampiezza" e la "intensità" della oscillazione provocata da un'onda generica, in un dato punto dello spazio e in funzione del tempo. Per vederne il significato nella pratica, vi propongo di "pensare" a una breve uscita in mare. Il mare monta, l’altezza (che possiamo anche dire ampiezza) delle onde raddoppia, senza che per fortuna l’onda si rompa. Il timore quadruplica in intensità, perché è collegato alla grandezza fisica che caratterizza l'impatto dell'onda: l’energia trasportata dal moto ondoso. In generale, una trattazione matematica completa porta a concludere che l'intensità (sempre positiva) di un'onda è proporzionale al quadrato della sua ampiezza (oscillante). L'andar per mare può aiutare a capire la Fisica.
............................................................................................................
Fig. 6. Ampiezza e intensità di un'onda
Immagine School Physics
..... ...............................................................................
Fig. 7. Un esperimento pensato sulla conservazione della quantità di moto
Arbor Scientific (2013) - Immagine Arbor Scientific
La doppia fenditura in esperimenti pensati
Dal punto di vista del meccanismo di formazione dell'interferenza, l'apparato di Young, il reticolo cristallino di Davisson e Germer e gli atomi nella sottile lamina d’oro di Thomson sono concettualmente equivalenti a un apparato ideale detto "doppia fenditura", implicitamente assunto di scala dimensionale atta a evidenziare fenomeni diffrattivi .
In quel capolavoro di divulgazione scientifica che è il Dialogo sopra i due massimi sistemi del mondo (pubblicato nel 1632), Galileo Galilei espone il suo concetto di relatività facendo pensare il lettore a un "navilio" all’interno del quale delle farfalle volano senza accorgersi del suo moto relativamente al mondo circostante. Potete trarre piacere dalla lettura di una trascrizione parziale del bellissimo testo di Galileo su Simmetrie e Relatività Speciale .
Il navilio di Galileo è uno storico esempio di “ esperimento pensato ” (noto con la denominazione tedesca "gedanken experiment"). Un esperimento pensato, non necessariamente realistico ma aderente alla sostanza del fenomeno, può costituire un efficace strumento per capire e far capire. Con perfida ironia, la figura 7 ne fornisce un esempio.
Le figure 8 e 9 sono tratte dalla preziosa Fisica di Feynman e rappresentano esperimenti pensati semplici e incisivi, metodologicamente basati sul concetto di esperimento con doppia fenditura applicato a onde e particelle. Seguiremo la traccia data da Richard Feynman . Vale la pena non sottrarsi al fascino della sua personalità e ascoltarne una viva lezione sull'argomento qui trattato, disponibile sul Web. Se vi capita, leggete i libri di divulgazione scientifica e qualsiasi cosa egli abbia scritto, non solo su argomenti di Fisica. Quello che accade con onde e particelle può essere visto anche in una animazione visibile sul Web, o in una fantasiosa lezione del Dr. Quantum . In italiano, sono disponibili le diapositive di un seminario "fatto in casa" e collegato a questo sito Web.
Fig. 8. Onde su fenditure (da La Fisica di Feynman)
Onde elettromagnetiche su doppia fenditura
La figura 8 illustra schematicamente cosa accade quando delle onde (per ora di qualsiasi natura) investono una doppia (1 e 2) fenditura caratterizzata da una scala dimensionale a distanza paragonabile alla lunghezza d'onda. Su un piano di osservazione (absorber) oltre le fenditure, l'intensità I 12 del segnale con ambedue le fenditure aperte mostra le frange d'interferenza tipiche delle onde (c in figura. Il motivo fisico - riflesso nella struttura matematica - è che si sommano le ampiezze h 1 e h 2 (h sta per l'inglese height, altezza) del segnale con solo l'una o l'altra delle fenditure aperte, e non le rispettive intensità I 1 e I 2 (b in figura
.
Focalizziamo l'attenzione sulle onde elettromagnetiche (vedete Interazione Elettromagnetica "alla Feynman" ) e domandiamoci se questo comportamento persista quando l'intensità della sorgente è ridotta indefinitamente. A un certo punto si inizia a vedere che il segnale non è continuo. Esso arriva a colpi, sotto forma di singoli punti luminosi sul piano di osservazione se questo è uno schermo con la proprietà di emettere luce quando colpito. Si osservano singoli "quanti". I quanti osservati sono della stessa natura di quelli che provocano l'effetto fotoelettrico. Come nell'effetto fotoelettrico, la fisica classica è superata: le onde elettromagnetiche sono anche particelle, chiamate " fotoni ".
Incuriositi, continuiamo ad accumulare punti luminosi sullo schermo. Quello che accade diventa proprio incredibile. I quanti arrivano a colpi come particelle e in base alla loro concezione classica ci attenderemmo che essi attraversino l'una o l'altra fenditura, fornendo un segnale complessivo uguale a I 1 + I 2 . Non è così. I singoli quanti si distribuiscono automaticamente uno dopo l'altro in bande separate da zone vuote, e l'immagine che si va costruendo assomiglia sempre più alla classica figura di interferenza I 12 osservata per le onde. I singoli quanti mantengono anche un comportamento da onda. E' come se un singolo quanto attraversasse “ambedue” le fenditure al pari di un'onda, interferendo con sé stesso in modo che colpo dopo colpo si formino le classiche frange d'interferenza.
In sintesi, le onde elettromagnetiche sono costituite da quanti, che arrivano a colpi come particelle ma danno luogo a interferenza come onde. Per dirla come Massimo Troisi in Pensavo fosse amore... invece era un calesse , ma con ritorno di fiamma: pensavamo che fossero onde e sono particelle, e queste si comportano anche da onda. Di primo acchito possono sembrare giochi di parole e confondere. In realtà rappresentano l'integrazione dei concetti di onda e particella in un unico cerchio alla yin e yang della quale si è parlato inizialmente, abitualmente chiamata dualismo anche se questa denominazione può non contribuire alla chiarezza.
Questo per quanto riguarda il fotone, nato da un'onda come la Venere del Botticelli . Curiosità impone.di vedere come l'elettrone, nato come particella "alla Democrito ", si comporta con una doppia fenditura. Troveremo simmetria?
Fig. 9. Elettroni su fenditure (da La Fisica di Feynman)
Elettroni su doppia fenditura
Rivolgiamo ora l'attenzione sulla figura 9, dove consideriamo che la doppia fenditura sia investita da particelle con credenziali doc: elettroni. Partendo da una configurazione nella quale essi si comportano da particelle, “immaginiamo" di diminuire progressivamente le fenditure in larghezza e distanza.
Abbiamo una grossa sorpresa: a un certo punto appaiono frange d’interferenza come mostrato in (c), in modo puramente indicativo. Dalla distanza tra le frange si può anche dedurre una lunghezza d’onda λ associata agli elettroni e scoprire che essa è legata all'inverso della loro quantità di moto p da una costante moltiplicativa, di nuovo la costante h di Planck: λ = h / p come nell' ipotesi ondulatoria di de Broglie. È come se lo stesso elettrone passasse attraverso ambedue le fenditure. La figura 10 mostra quanto questo sia paradossale nella visione classica: se il treno avesse un comportamento quantistico, dovrebbe tranquillamente poter passare attraverso ambedue i tunnel.
...........................................
Fig. 10. Se un treno si comportasse come un elettrone
Immagine The Mysearch Website..... ..................................
Fig. 11. Animazione con elettroni (o singoli fotoni) su doppia fenditura
Immagine Wikipedia
Abbiamo detto “immaginiamo” e abbiamo così approfittato dei vantaggi degli esperimenti pensati. Continuando con l'immaginazione, registriamo uno a uno l'impatto dei singoli elettroni. Come i singoli fotoni di cui sopra, vediamo gli elettroni accumularsi formando man mano frange di interferenza. Lo mostra l'animazione in figura 11, che potrebbe anche essere riferita al comportamento di singoli fotoni precedentemente descritto. Vi è simmetria tra elettroni e fotoni. Per entrambi le due rappresentazioni possono concettualmente coesistere: essi sono onde "e" particelle. La fisica classica è superata: in essa l'essere onda "oppure" particella sono mutualmente esclusivi.
È difficilissimo passare da un esperimento pensato a uno reale, con registrazione di elettroni singoli. Le fenditure devono avere dimensioni e distanze straordinariamente piccole: la grandezza di riferimento è la lunghezza d'onda di de Broglie dell'elettrone, la quale risente del piccolissimo valore della costante di Planck. Ma nel 1976 con raffinatissimi accorgimenti l’esperimento fu realmente eseguito all’Università di Bologna e fu vista l' interferenza quantistica di singoli elettroni .
Indeterminazione e probabilità: Oh Alice ... Ma Bob...
Le sorprese si aggiungono alle sorprese. Immaginiamo di riuscire, in qualche modo, a determinare da quale delle due fenditure l'elettrone sia passato: l'interferenza scompare. Se osservato, l’elettrone fa come i bambini e si comporta da "brava particella". In termini scientifici, il suo comportamento da onda è collegato alla "indeterminazione" nella fenditura dalla quale è passato. È una manifestazione del principio di indeterminazione, del quale abbiamo già parlato, Possiamo solo assegnare una "probabilità" al passaggio attraverso ciascuna delle fenditure. Due nuove parole entrano nella rigorosa Fisica al livello fondamentale: "indeterminazione" e "probabilità". Con esse, la costante h di Planck ha colpito ancora. Le certezze e realtà assolute ottocentesche - con i loro risvolti di arroganza da parte delle piccole menti - sono ora sanamente mutate in realtà probabilistiche, come in altri campi del sapere, nella vita personale e nell'evoluzione di sistemi complessi quale è per esempio la società umana: la Fisica si è umanizzata.
I paradossi fanno capire la portata rivoluzionaria di nuove visioni della Scienza, non solo in quanto qui discusso (vedete per esempio Simmetrie e Relatività Speciale ). L'ironia usa spesso lo stesso strumento, come mostra la figura 12.
Fig. 12. Oh Alice ... tu sei la donna per la mia vita
Ma Bob ... in un mondo quantistico come puoi esserne sicuro?
Immagine Physics Intuition Applications
Meccanica Quantistica: probabilità
Dice Feynman nelle sue lezioni già citate parlando degli esperimenti descritti sopra, concettualmente chiamati "su doppia fenditura":
“We choose to examine a phenomenon which is impossible, absolutely impossible, to explain in any classical way, and which has in it the heart of Quantum Mechanics. In reality, it contains the only mystery"
(Scegliamo di esaminare un fenomeno che è impossibile, assolutamente impossibile , spiegare in alcun modo classico, e che ha in sé il cuore della Meccanica Quantistica. In realtà, esso contiene l'unico mistero).
Questa sorprendente rivoluzione concettuale pose la sfida scientifica di inquadrarla in una struttura matematica coerente. Come prima cosa, che fare ora che il principio di indeterminazione ci impedisce di dire che una particella "ha" certe coordinate spaziali e una certa quantità di moto? Dobbiamo trattarla come un'onda "e" in termini probabilistici. La figura 6 viene in soccorso, dando la "dritta". In primo luogo, la probabilità deve essere sempre positiva: non può che corrispondere a quella che in fisica classica è l'intensità dell'onda, precedentemente definita come il quadrato dell'ampiezza. Sempre iniziando con un riferimento alla fisica classica, i meccanismi dei fenomeni sono descritti ragionando sull'ampiezza: come potrebbero altrimenti le intensità (sempre positive) di due onde sommarsi algebricamente e dar luogo non solo a interferenza costruttiva, ma anche distruttiva?
Meccanica Quantistica: ampiezza di probabilità
Da quanto detto sopra si può capire che anche in Meccanica Quantistica per la descrizione dei fenomeni si deve ragionare sull'ampiezza. Essa assume il nome di "ampiezza di probabilità" per caratterizzarne la connessione con una probabilità, data da un'operazione che nell'appropriato formalismo matematico corrisponde a un'elevazione a potenza al quadrato, proprio come per le onde in figura 6.
Si è precedentemente detto che il comportamento di una particella come l'elettrone è descritto dall'Equazione di Schrödinger o, in maniera più completa, dall'equazione di Dirac, Va da sè che esse operano su "ampiezze di probabilità". Le loro soluzioni sono dette " funzioni d'onda ". Lo sono gli orbitali che descrivono lo stato di un elettrone in un atomo in corrispondenza di specifici "numeri quantici" (vedete Da linee di Fraunhofer ad atomo quantistico ). Un esempio di orbitale è dato in figura 13, che mostra la distribuzione di probabilità sotto forma di "nube elettronica".
.................................................................... Fig. 13. La nube elettronica dell’orbitale
1s dell’atomo di Idrogeno
Immagine La Chimica di Atkins - Zanichelli....... .......................................
Fig. 14. Gli stati stazionari delle corde vibranti
Immagine Univ. Wisconsin Platteville
Riflettendo, un orbitale non rappresenta un elettrone singolo, ma piuttosto l'elettrone nel "sistema atomo", con funzione d'onda determinata dal legame con il nucleo. Che dire di una particella libera, elettrone, fotone o altra che sia? La figura 6 viene di nuovo in soccorso. L'onda che mostra può essere vista come rappresentazione di un caso limite contemplato dal principio di indeterminazione, ove la costante di Planck fissa il prodotto delle indeterminazioni di variabili correlate. Nella figura, la lunghezza d'onda è perfettamente determinata e con essa la quantità di moto, le due grandezze essendo legate dalla relazione di de Broglie λ = h / p. La grandezza fisica correlata la quantità di moto nel principio di indeterminazione è la posizione, che infatti in figura 6 è totalmente indeterminata: l'onda si estende all'infinito. L'altro caso limite è quello di posizione perfettamente determinata, e quantità di moto totalmente indeterminata. I casi intermedi sono descritti da "pacchetti di onde", costituiti dalla sovrapposizione di onde aventi lunghezza d'onda addensate attorno a un valore centrale. Essi sono evocati nella rappresentazione data ai fotoni incidenti in figura 3.
Musica, timbro e modi normali
La Musica è vibrazione e trasmissione di onde sonore che fanno vibrare timpani e anima. La fisica della musica porta a riflettere su concetti di validità più generale. La figura 14 mostra che le vibrazioni di una corda (per esempio di violino) fissata alle estremità sono caratterizzate dalle presenza delle cosiddette “ onde stazionarie ”. Per definizione esse si mantengono invariate nel tempo, facendo astrazione da fenomeni dissipativi. Le onde stazionarie sono “quantizzate”: la lunghezza d’onda λ può assumere solo determinati valori, con la lunghezza l della corda multiplo di ½ λ. Le onde stazionarie corrispondono alle “armoniche” del linguaggio musicale e ai cosiddetti "modi normali" di oscillazione del linguaggio fisico. A ognuno di esse corrisponde una determinata frequenza.
Risuonando, il corpo (cassa armonica in un violino ) di uno strumento musicale amplifica ed esalta in modo diverso le varie armoniche secondo la loro frequenza. La distribuzione in frequenza complessiva è detta “spettro”. Se lo strumento emettesse una sola frequenza sarebbe come un diapason , che serve ma non fa musica. La ricchezza del suono emesso proviene proprio dalla “ sovrapposizione ” delle varie armoniche, ciascuna presente in una certa misura. Il cosiddetto “ timbro ” è determinato dal contenuto spettrale del suono e dalla sua evoluzione nel tempo. Per approfondimenti, vedete Il suono sul testo online La Fisica di Amaldi o il sito Web Fisica Onde Musica , molto completo.
Stati e autostati quantistici
Con le dovute differenze, in Meccanica Quantistica si può ragionare in modo analogo. Il “principio di sovrapposizione” dice che lo stato di una particella o di un sistema può essere rappresentato dalla sovrapposizione delle ampiezze di probabilità corrispondenti a un certo numero di “stati quantistici di base", scelti secondo opportuni criteri e sommati secondo le appropriate regole. La scelta razionale degli quantistici di base cade sui cosiddetti “autostati". Essi sono i corrispondenti quantistici dei modi normali di una corda vibrante, nel senso che in assenza di perturbazioni essi si mantengono nel tempo. Per esempio, gli orbitali elettronici in un atomo sono autostati, definiti da specifici numeri quantici. In questo modo, nell'evoluzione del processo non variano gli autostati ma solo la loro proporzione nella sovrapposizione.
Meccanica Quantistica e fisica classica
In linea di principio, la Meccanica Quantistica ha validità generale e non ristretta al mondo delle particelle elementari. Esperimenti recenti hanno mostrato che il comportamento onda-particella vale anche per molecole, anche grandi. Ma si può andare oltre, almeno in linea di principio. Come si è visto, la lunghezza d'onda è inversamente proporzionale alla quantità di moto: nel mondo macroscopico della fisica classica, masse e quantità di moto sono enormi rispetto a quelle delle particelle. Di conseguenza, le lunghezze d'onda sono talmente piccole da rendere totalmente invisibile ogni effetto quantistico. La Meccanica Quantistica è totalmente compatibile con la fisica classica, che resta una valida approssimazione nella sua " riserva indiana ".
Oggi e domani
La rivoluzione scientifica iniziata con il Novecento impatta molto fortemente sulla nostra vita pratica.
Senza la Relatività, il navigatore non vi aiuterebbe a trovare la buona pizzeria ove volete andare: il funzionamento del GPS richiede che si tenga conto della Relatività, sia Ristretta che Generale. Per esempio, se trascurassimo la Relatività Generale, un GPS che desse la correttamente posizione ad un certo istante, dopo un giorno sbaglierebbe di 10 km.
La Meccanica Quantistica-Ondulatoria ha invaso la nostra vita con le sue applicazioni tecnologiche e gli svariatissimi dispositivi elettronici oggi dilaganti, a cominciare da quella specie di protesi chiamata telefonino. E non avremmo neppure il laser, ormai infilato dappertutto anche all'insaputa di molti (vedete ad esempio Da Alan Turing al calcolo quantistico e Laser e Ottica Quantistica ).
..........................................
Fig. 15. La Programma 101 della Olivetti
Immagine Museo Nazionale della Scienza e della Tecnologia L. da Vinci..... ..............................................
Fig. 16. Il microprocessore Intel 8742
Immagine Wikiwand
Il progresso prosegue a ritmo rapidissimo. Considerando ad esempio il calcolo, pochi riferimenti bastano a testimoniarlo. La figura 15 mostra la Programma 101 della Olivetti, che fu il primo calcolatore da tavolo programmabile del mondo e fu posto in commercio nel 1965. I nostri attuali calcolatori utilizzano “microprocessori”. Il primo a essere commercializzato fu l’ Intel 4004 , nel 1971. La Apple I uscì nel 1976, approfittando dell'era della microelettronica e con importanti innovazioni comprendenti in primo luogo l'aggiunta di un visore. I microprocessori di oggi includono diversi componenti a un altissimo livello di integrazione, con la presenza di oltre un miliardo di elementi. La figura 16 mostra l' Intel 8742 . E ci sia avvia verso il "calcolo quantistico", del quale tratta Da Alan Turing al calcolo quantistico .
Ragazzi di oggi, mettetevi al passo.
Collegamenti e bibliografia
Peter Atkins e Loretta Jones, Gli atomi: il mondo quantico , La Chimica di Atkins, W.H. Freeman - Zanichelli (2007, testo su Web)
R.P. Feynman, R.B. Leighton e M. Sands, La Fisica di Feynman (The Feynman’s Lectures on Physics), Vol. 3, Cap. 1, Addison Wesley - Zanichelli (1965)
Ringrazio il "nostro amico" Crisostomo Sciacca per vari suggerimenti e per aver così messo ancor più in evidenza il fascino e il mistero di questa Fisica.
Paolo Strolin
.
.
.
Ultima Modifica 5 Anni 2 Mesi fa da Paolo.
Si prega Accesso a partecipare alla conversazione.
Tempo creazione pagina: 0.901 secondi