- Messaggi: 1
- Ringraziamenti ricevuti 0
Asimmetrie al grandangolare
- Asimmetrie
-
Autore della discussione
- Offline
- Nuovo Utente
-

Less
Di più
12 Anni 2 Mesi fa - 8 Anni 11 Mesi fa #108
da Asimmetrie
Si ha asimmetria chirale, o “ chiralità ”, se un enantiomero non esiste o è meno frequente. La chiralità è largamente diffusa in Natura. Ad esempio, anche una chiocciola con la sua forma elicoidale presenta generalmente un enantiomero preferito, il destrorso o il sinistrorso.
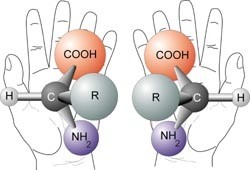
Le proprietà chirali di una molecola organica (quale per esempio un ammino-acido, costituente delle proteine e mostrato in figura 3) hanno effetti pratici: per esempio, esse influenzano il senso (destrogiro o levogiro) in cui la molecola ruota il piano di polarizzazione della luce. Attraverso quale meccanismo naturale si giunge alla differenziazione degli enantiomeri?
Un tale interrogativo è di carattere generale, e vale anche in Fisica: lo vedremo perfino parlando del mistero dell’antimateria scomparsa dai primordi dell’Universo a oggi, intanto anticipandovi figura 4. Questo e altro motiva il parlare di farfalle, mani, chiocciole e Fisica in un unico contesto di Asimmetrie.
E' quindi errato l'usuale ritenere che una riflessione implichi un'inversione delle coordinate destra-sinistra. Matematicamente, una riflessione corrisponde invece a un'inversione della coordinata rivolta in direzione perpendicolare allo specchio.
La figura 6 mostra la riflessione speculare di una palla da tennis in rotazione: nell'immagine speculare, il senso di rotazione è invertito.
Trasformazioni discrete per particelle
Come detto in Simmetrie: dai solidi platonici ai cristalli minerali , Simmetria significa Invarianza rispetto a una specifica trasformazione. Illustriamo le trasformazioni che interessano particolarmente la fisica delle particelle elementari. Esse sono trasformazioni “discrete”, cioè non continue ma a passi.
....................................................
Fig. 8. Le trasformazioni P, CP e T, da sinistra a destra - Immagine Quantum Diaries
La “trasformazione di Parità” P implica l'inversione di tutte le coordinate spaziali, come mostrato in figura 7. La figura 8 a sinistra mostra che essa inverte il senso di rotazione da sinistrorso (left handed) a destrorso (right handed) e viceversa. La riflessione speculare ha lo stesso effetto, pur implicando l'inversione della sola coordinata perpendicolare allo specchio: essa può essere utile per illustrare graficamente una trasformazione di Parità, con la quale non va tuttavia confusa.
In fisica classica, un momento angolare è matematicamente dato dal prodotto vettoriale di velocità e distanza vettoriale dall'asse di rotazione: ambedue cambiano verso a seguito di una La “trasformazione di Parità e quindi quello del momento angolare resta immutato. Resta immutato anche il momento angolare di "spin" (vedete Lo spin ), indicato in figura 8 dalla freccia verticale.
La "Coniugazione di carica" C consiste nel trasformare un processo fisico ridefinendo le particelle come anti-particelle, e viceversa. Per esempio, un elettrone è ridefinito come positrone e, di conseguenza, cambia il segno della carica elettrica.
La "Trasformazione CP" implica l'applicazione combinata delle trasformazioni C e P. La figura 8 al centro ne mostra l'effetto su un elettrone.
La "Inversione temporale T" corrisponde nientemeno che a considerare un processo per cui il tempo scorre in direzione opposta. La figura 8 a destra mostra che l'effetto su una particella è l'inversione del senso di rotazione e quindi del momento angolare di spin.
Infine, la "Trasformazione CPT" implica l'applicazione combinata delle trasformazioni C, P e T.
Violazioni di simmetria nei processi fisici
Con riferimento all'articolo Simmetrie: dai solidi platonici ai cristalli minerali , ricordiamo che i concetti di Simmetria e di Invarianza rispetto a una trasformazione sono sostanzialmente equivalenti. Per un processo fisico, si ha simmetria se quello ottenuto applicando la trasformazione corrisponde a una possibile realtà, cioè se potrebbe in linea di principio aver luogo. Altrimenti si ha "violazione della simmetria" o, in altre parole, "asimmetria".
Si noti che si può parlare nello stesso modo di qualunque cosa si parli e per qualsiasi trasformazione. Ad esempio, si ha violazione di simmetria chirale se i due enantiomeri non sono egualmente diffusi.
L’unico vincolo teorico a una simmetria rispetto alle trasformazioni presentate sopra è dato dal “ Teorema CPT ”. Esso richiede la conservazione della simmetria CPT per tutti i fenomeni fisici, assumendo la correttezza delle attuali leggi quantistiche e l' Invarianza di Lorentz . Tuttavia, in senso assoluto, il Teorema CPT è da verificare sperimentalmente.
Anche la Fisica ha un peccato originale?
Salviati, il portavoce della scienza galileiana, nella Prima Giornata dei Discorsi e dimostrazioni matematiche intorno a due nuove scienze (1638) di Galileo Galilei (1564-1642) dice:
“È (torno a dire) l'intento mio dichiarare, come delle diverse velocità di mobili di differente gravità non ne sia altramente causa la diversa gravità, ma che ciò dependa da accidenti esteriori ed in particolare dalla resistenza del mezzo, sì che, tolta questa, tutti i mobili si moverebber con i medesimi gradi di velocità”.
Galileo Galilei ci ha così abituati a definire le leggi fondamentali della Fisica sfrondando i fenomeni da effetti estranei, quali l'attrito nella caduta dei gravi. Guardiamo quindi la figura 10 con gli occhi di Galileo e con il linguaggio di oggi. Il fatto che lo skateboarder possa risalire dall'altra parte alla stessa altezza - attrito e cadute a parte - indica che vale la simmetria rispetto all'inversione temporale, che vede la risalita come il processo nel quale è trasformata la discesa.
Considerazioni di questo genere valgono in generale: ad esempio - di nuovo considerando un esempio relativo all'inversione temporale e sempre in assenza ideale di attrito e di altri effetti estranei al fenomeno - un proiettile sparato indietro ripercorre la stessa traiettoria. In sostanza, la fisica classica ha definito le sue leggi a livello fondamentale auto-affrancandosi dalle asimmetrie che vediamo altrove in Natura, come sopra evocato. Le asimmetrie nascono da effetti a livello contingente e non fondamentale, quale è l'attrito.
Evidenziamo con la figura 11 un interrogativo importante: le asimmetrie sono veramente un "peccato originale" da cui la Fisica è esente, a livello fondamentale? O sono piuttosto una caratteristica generale in Natura?
Dal neutrino la prima scossa al sistema
Iniziamo da chiodi e da viti. Un chiodo non cambia per trasformazione di Parità: la simmetria è rispettata. Una trasformazione di Parità porta da una vite commerciale (destrorsa) a una vite sinistrorsa, che non esiste sul mercato: le viti commerciali violano la simmetria rispetto alla Parità.
Le particelle elementari con spin nullo sono assimilabili a chiodi. Quelle con spin non nullo sono assimilabili a viti ideali, le quali in linea di principio possono essere destrorse o sinistrorse.
Fu la prima scossa al sistema, e di magnitudine da far saltare i sismografi. Anche la Fisica a livello fondamentale ha peccato originale. O piuttosto l'Asimmetria non è peccato: la Natura è fatta così.
Gli articoli
Nel presentare brevemente gli articoli, prima di focalizzare l’attenzione sulla Fisica volgiamo alle Asimmetrie nei campi della Scienza che si rivolgono al mondo organico.
Asimmetrie: La Chiralità negli organismi viventi parla di simmetrie e asimmetrie chirali negli organismi viventi. Inizia riferendosi a oggetti di uso comune (come viti o eliche) per avviare un discorso sugli esseri viventi pure caratterizzati da “elicità”, per esempio le chiocciole. Discute le più comuni simmetrie nei viventi, quelle destra-sinistra, facendo infine osservare come queste simmetrie siano solo apparenti e in ultima analisi i viventi siano asimmetrici.
Asimmetrie: La chiralità in Chimica spiega come una asimmetria chirale si ritrovi anche a livello delle molecole. In particolare la presentano molti composti essenziali per la vita: proteine, zuccheri, DNA. Una molecola di chiralità opposta a quella richiesta (ad esempio sinistra invece di destra) non può inserirsi nell'organismo: sebbene i due enantiomeri abbiano in linea di principio le stesse proprietà, negli organismi la Natura ha fatto una scelta che li rende differenti. Si discute anche della possibile causa di questa rottura di simmetria.
Asimmetrie: violazione della Parità e neutrino allo specchio tratta della scoperta della violazione della simmetria per trasformazione di "Parità" in un processo di Interazione Debole (vedete Interazione Debole ), con il neutrino come primo (invisibile) protagonista. Essendo soggetto solo a quest'interazione, il neutrino è particolarmente atto al suo studio e ha portato alla ribalta la totale violazione di Parità che lo caratterizza. Come detto precedentemente, la scoperta di un’asimmetria al livello fondamentale delle particelle elementari e delle loro interazioni fu fatto totalmente nuovo e sensazionale. Con la violazione della Parità, le Asimmetrie penetrano nel mondo delle particelle e si manifestano come un fenomeno naturale di carattere generale.
Asimmetrie: come fu scoperta la violazione della Parità descrive il famoso esperimento che portò alla scoperta della violazione della Parità nell’Interazione Debole.
Asimmetrie: CP, tempo e antimateria scomparsa parla di una piccola ma importantissima asimmetria nelle Interazioni Deboli, la cosiddetta "violazione di CP". Come detto sopra, si può supporre che la simmetria CPT sia conservata. La violazione di CP ha quindi come conseguenza un'asimmetria per inversione T a livello fondamentale, superando la visione galileiana. Inoltre essa implica un diverso comportamento di materia e antimateria e quindi incide sul mistero della scomparsa dell’antimateria dagli istanti iniziali dell’Universo a oggi e della praticamente totale asimmetria materia-antimateria che riscontriamo attualmente.
Rottura Spontanea della Simmetria inizia introducendone il concetto, per poi illustrarne qualitativamente il ruolo nel meccanismo teorico secondo cui la presenza del "bosone di Higgs" (vedete Il bosone di Higgs: una rivoluzione rispetto al comune pensare è necessaria affinché le particelle elementari e i mediatori delle loro interazioni acquisiscano una massa finita.
Riferimenti bibliografici
La Fisica di Feynman (Simmetria nelle leggi fisiche, Vol 1, Cap. 52) regala sempre una lettura illuminante, in ogni tempo e stagione. Nella rivista Asimmetrie ( numero 11, 2011 ) potete trovare un insieme di articoli dedicati a Simmetrie e Asimmetrie nei loro diversi aspetti e attualità. Una rassegna approfondita è condotta da Franco Strocchi in Simmetrie e rotture di simmetrie in Fisica . Vi segnaliamo anche un articolo su Quantum Diaries : Symmetry in Physics, Part 2: Discrete Symmetries and Antimatter .
...
...
Asimmetrie al grandangolare è stato creato da Asimmetrie
Asimmetrie al grandangolare
......................
................
Per domande: autori o
Domanda a un esperto
................| ........................................................................... Fig. 1. Coppa in terracotta del medio periodo Jomon (Giappone, circa 3000 a.C.) Metropolitan Museum of Art, New York Immagine Metropolitan Museum of Art .................... .................... Fig. 2. Lottatori, bronzetto nuragico (830-750 a.C.) Provenienza Monte Arcosu, Uta - Museo Nazionale, Cagliari Immagine Rotary Club Quartu Sant’Elena | ....... | ........................................................................................... Nell'articolo Simmetrie: dai solidi platonici alla struttura cristallina abbiamo iniziato a parlare di Simmetrie ammirando la perfetta e armoniosa simmetria di una coppa attica a figure nere dalla Grecia del VI secolo avanti Cristo. Essa mostra come la cultura occidentale abbia tradizionalmente curato la Simmetria, portatrice di equilibrio. Ora ammiriamo in figura 1 la singolare bellezza della terracotta giapponese del periodo Jomon , anzitutto stupiti nel constatare quali raffinatissimi capolavori sono stati realizzati in epoche tendenzialmente considerate come primitive. La terracotta Jomon esprime l’antica sensibilità della cultura orientale al fascino delle Asimmetrie. Già il corpo presenta leggere asimmetrie. Le onde aeree e armoniose del suo asimmetrico coronamento accarezzano gli occhi. La sua sciolta evoluzione spaziale sfugge allo statico equilibrio della Simmetria ed evoca piuttosto divenire temporale e differenziazione. Il bronzetto nuragico in figura 2 illustra in modo simbolico come nella vita corrente a partire da stati simmetrici un'asimmetria nelle forze porta al prevalere del più forte e a una situazione essa stessa asimmetrica. Qualcosa del genere avviene anche in Natura, per un processo evolutivo che porta a una asimmetria. In altri casi una simmetria prevede stati che nella realtà non sono popolati, per cui l'asimmetria esiste a priori. Vedremo degli esempi nella serie di articoli sul ruolo dell’Asimmetria in Natura, che presentiamo brevemente nel seguito. Vedremo anche che il carattere unificante della Scienza emerge quando ci si eleva dal particolare e ci si rivolge ai grandi temi, come Simmetrie e Asimmetrie. Farfalle, mani, chiocciole e antimateria Le ali di una farfalla sono simmetriche rispetto al suo piano mediano. Esse hanno la stessa simmetria delle nostre mani e si dice che esse hanno “simmetria chirale” (dalla parola greca χειρ che significa "mano"). Le due ali di farfalla, come le mani, sono identiche ma non sovrapponibili. I due stati collegati da simmetria chirale sono detti “enantiomeri”. Il collegamento consiste nel fatto che essi possono essere "trasformati" uno nell'altro mediante una riflessione speculare. Nel caso delle ali di una farfalla, potete immaginare che essa avvenga in uno specchio ideale coincidente con il suo piano mediano. |
Si ha asimmetria chirale, o “ chiralità ”, se un enantiomero non esiste o è meno frequente. La chiralità è largamente diffusa in Natura. Ad esempio, anche una chiocciola con la sua forma elicoidale presenta generalmente un enantiomero preferito, il destrorso o il sinistrorso.
| ............................................................... .................... .................... .................... Fig. 3. Rappresentazione schematica della chiralità di un ammino-acido Immagine Physical Methods in Chemistry and Nano Science | ... | ...............................................................
Fig. 4. H.R. Quinn e Y. Mir Il mistero dell’antimateria scomparsa Princeton Hardcover (2007) - Immagine Amazon |
Le proprietà chirali di una molecola organica (quale per esempio un ammino-acido, costituente delle proteine e mostrato in figura 3) hanno effetti pratici: per esempio, esse influenzano il senso (destrogiro o levogiro) in cui la molecola ruota il piano di polarizzazione della luce. Attraverso quale meccanismo naturale si giunge alla differenziazione degli enantiomeri?
Un tale interrogativo è di carattere generale, e vale anche in Fisica: lo vedremo perfino parlando del mistero dell’antimateria scomparsa dai primordi dell’Universo a oggi, intanto anticipandovi figura 4. Questo e altro motiva il parlare di farfalle, mani, chiocciole e Fisica in un unico contesto di Asimmetrie.
| .................................................................
Fig. 5. Perché non così? Immagine Penapai - Neutrino Science | ..... | .................................................... Riflessione speculare Ci specchiamo (quasi) tutti i giorni, ma abbiamo veramente capito come funziona la simmetria per riflessione speculare? Lo specchio - chiodo e cornice a parte - ha totale simmetria destra-sinistra come alto-basso. Ma allora perché nell'immagine speculare la mano destra appare come sinistra, ma la testa non appare in basso e i piedi in alto come in figura 5? E' fortuna o razionalità scientifica? Potete ascoltare la risposta nientemeno che da Richard Feynman (1918-88) nel video Fun to imagine: mirrors (Divertente immaginare: specchi). Sullo slancio, potete anche scientificamente curiosare nell'intera serie a lui dedicata dall'inglese BBC: Fun to imagine: using physics to explain how the world works (Divertente immaginare: usando la fisica per spiegare come funziona il mondo). In poche parole, una riflessione "sembra" scambiare destra con sinistra e non testa con piedi semplicemente perché le mani sono enantiomeri, testa e piedi invece no. Per averne una riprova, immaginatevi sdraiati per terra in una stanza con uno specchio al soffitto: nulla cambia se ruotate la vostra posizione. |
E' quindi errato l'usuale ritenere che una riflessione implichi un'inversione delle coordinate destra-sinistra. Matematicamente, una riflessione corrisponde invece a un'inversione della coordinata rivolta in direzione perpendicolare allo specchio.
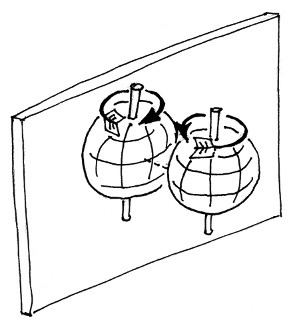
La figura 6 mostra la riflessione speculare di una palla da tennis in rotazione: nell'immagine speculare, il senso di rotazione è invertito.
| .................................
Fig. 6. La riflessione in uno specchio inverte il senso di rotazione - Immagine: Luca Lista | ... | ....................................................
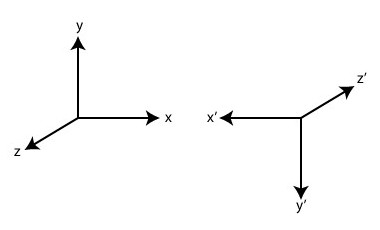
Fig. 7. La trasformazione di Parità Immagine Quantum Diaries |
Trasformazioni discrete per particelle
Come detto in Simmetrie: dai solidi platonici ai cristalli minerali , Simmetria significa Invarianza rispetto a una specifica trasformazione. Illustriamo le trasformazioni che interessano particolarmente la fisica delle particelle elementari. Esse sono trasformazioni “discrete”, cioè non continue ma a passi.
....................................................
Fig. 8. Le trasformazioni P, CP e T, da sinistra a destra - Immagine Quantum Diaries
La “trasformazione di Parità” P implica l'inversione di tutte le coordinate spaziali, come mostrato in figura 7. La figura 8 a sinistra mostra che essa inverte il senso di rotazione da sinistrorso (left handed) a destrorso (right handed) e viceversa. La riflessione speculare ha lo stesso effetto, pur implicando l'inversione della sola coordinata perpendicolare allo specchio: essa può essere utile per illustrare graficamente una trasformazione di Parità, con la quale non va tuttavia confusa.
In fisica classica, un momento angolare è matematicamente dato dal prodotto vettoriale di velocità e distanza vettoriale dall'asse di rotazione: ambedue cambiano verso a seguito di una La “trasformazione di Parità e quindi quello del momento angolare resta immutato. Resta immutato anche il momento angolare di "spin" (vedete Lo spin ), indicato in figura 8 dalla freccia verticale.
| .................................................................................................
Fig. 9. L’elicità: destrorsa (a sinistra) se lo spin s ha lo stesso verso della quantità di moto p, sinistrorsa (a destra) se il verso è opposto. Immagine Wikipedia | ... | .................................................... Per le particelle, generalmente in moto, ci si riferisce alla "elicità" piuttosto che allo spin (vedete Spin e elicità dell’elementare ). Essa è definita come la proiezione dello spin lungo la direzione del moto. La figura 9 mostra che il verso dell'elicità può essere destrorso o sinistrorso: esso corrisponde a quello dell'avvitamento di una vite per la fisica classica. La trasformazione di Parità inverte la direzione del moto e con essa il verso dell’elicità. |
La "Coniugazione di carica" C consiste nel trasformare un processo fisico ridefinendo le particelle come anti-particelle, e viceversa. Per esempio, un elettrone è ridefinito come positrone e, di conseguenza, cambia il segno della carica elettrica.
La "Trasformazione CP" implica l'applicazione combinata delle trasformazioni C e P. La figura 8 al centro ne mostra l'effetto su un elettrone.
La "Inversione temporale T" corrisponde nientemeno che a considerare un processo per cui il tempo scorre in direzione opposta. La figura 8 a destra mostra che l'effetto su una particella è l'inversione del senso di rotazione e quindi del momento angolare di spin.
Infine, la "Trasformazione CPT" implica l'applicazione combinata delle trasformazioni C, P e T.
Violazioni di simmetria nei processi fisici
Con riferimento all'articolo Simmetrie: dai solidi platonici ai cristalli minerali , ricordiamo che i concetti di Simmetria e di Invarianza rispetto a una trasformazione sono sostanzialmente equivalenti. Per un processo fisico, si ha simmetria se quello ottenuto applicando la trasformazione corrisponde a una possibile realtà, cioè se potrebbe in linea di principio aver luogo. Altrimenti si ha "violazione della simmetria" o, in altre parole, "asimmetria".
Si noti che si può parlare nello stesso modo di qualunque cosa si parli e per qualsiasi trasformazione. Ad esempio, si ha violazione di simmetria chirale se i due enantiomeri non sono egualmente diffusi.
L’unico vincolo teorico a una simmetria rispetto alle trasformazioni presentate sopra è dato dal “ Teorema CPT ”. Esso richiede la conservazione della simmetria CPT per tutti i fenomeni fisici, assumendo la correttezza delle attuali leggi quantistiche e l' Invarianza di Lorentz . Tuttavia, in senso assoluto, il Teorema CPT è da verificare sperimentalmente.
|
Fig. 10. L'inversione del tempo nello skateboard Immagine Tumbir | ... |
Fig. 11. Eva e il peccato originale Monaco Pantaleone, mosaico pavimentale (1163-65) Cattedrale di Otranto , Lecce Immagine Ph. Ravi Sintra - Fame di Sud |
Anche la Fisica ha un peccato originale?
Salviati, il portavoce della scienza galileiana, nella Prima Giornata dei Discorsi e dimostrazioni matematiche intorno a due nuove scienze (1638) di Galileo Galilei (1564-1642) dice:
“È (torno a dire) l'intento mio dichiarare, come delle diverse velocità di mobili di differente gravità non ne sia altramente causa la diversa gravità, ma che ciò dependa da accidenti esteriori ed in particolare dalla resistenza del mezzo, sì che, tolta questa, tutti i mobili si moverebber con i medesimi gradi di velocità”.
Galileo Galilei ci ha così abituati a definire le leggi fondamentali della Fisica sfrondando i fenomeni da effetti estranei, quali l'attrito nella caduta dei gravi. Guardiamo quindi la figura 10 con gli occhi di Galileo e con il linguaggio di oggi. Il fatto che lo skateboarder possa risalire dall'altra parte alla stessa altezza - attrito e cadute a parte - indica che vale la simmetria rispetto all'inversione temporale, che vede la risalita come il processo nel quale è trasformata la discesa.
Considerazioni di questo genere valgono in generale: ad esempio - di nuovo considerando un esempio relativo all'inversione temporale e sempre in assenza ideale di attrito e di altri effetti estranei al fenomeno - un proiettile sparato indietro ripercorre la stessa traiettoria. In sostanza, la fisica classica ha definito le sue leggi a livello fondamentale auto-affrancandosi dalle asimmetrie che vediamo altrove in Natura, come sopra evocato. Le asimmetrie nascono da effetti a livello contingente e non fondamentale, quale è l'attrito.
Evidenziamo con la figura 11 un interrogativo importante: le asimmetrie sono veramente un "peccato originale" da cui la Fisica è esente, a livello fondamentale? O sono piuttosto una caratteristica generale in Natura?
Dal neutrino la prima scossa al sistema
Iniziamo da chiodi e da viti. Un chiodo non cambia per trasformazione di Parità: la simmetria è rispettata. Una trasformazione di Parità porta da una vite commerciale (destrorsa) a una vite sinistrorsa, che non esiste sul mercato: le viti commerciali violano la simmetria rispetto alla Parità.
Le particelle elementari con spin nullo sono assimilabili a chiodi. Quelle con spin non nullo sono assimilabili a viti ideali, le quali in linea di principio possono essere destrorse o sinistrorse.
| ........................................................................................................
Fig. 12. Palla da tennis in rotazione e neutrino allo specchio Immagine: Luca Lista | ....... | .......................................................... Come discusso in Asimmetrie: violazione della Parità e neutrino allo specchio , si è scoperto che i neutrini hanno la singolare proprietà di esser solo sinistrorsi e gli antineutrini solo destrorsi. Utilizzando la riflessione speculare solo per rappresentare graficamente la trasformazione di Parità, al contrario di una palla da tennis in rotazione un neutrino ν L (sinistrorso) non ha immagine (destrorsa) riflessa nello specchio che corrisponda a realtà fisica (figura 12). I neutrini sono assimilabili a viti commerciali e i processi che li coinvolgono violano totalmente la Parità. |
Fu la prima scossa al sistema, e di magnitudine da far saltare i sismografi. Anche la Fisica a livello fondamentale ha peccato originale. O piuttosto l'Asimmetria non è peccato: la Natura è fatta così.
Gli articoli
Nel presentare brevemente gli articoli, prima di focalizzare l’attenzione sulla Fisica volgiamo alle Asimmetrie nei campi della Scienza che si rivolgono al mondo organico.
Asimmetrie: La Chiralità negli organismi viventi parla di simmetrie e asimmetrie chirali negli organismi viventi. Inizia riferendosi a oggetti di uso comune (come viti o eliche) per avviare un discorso sugli esseri viventi pure caratterizzati da “elicità”, per esempio le chiocciole. Discute le più comuni simmetrie nei viventi, quelle destra-sinistra, facendo infine osservare come queste simmetrie siano solo apparenti e in ultima analisi i viventi siano asimmetrici.
Asimmetrie: La chiralità in Chimica spiega come una asimmetria chirale si ritrovi anche a livello delle molecole. In particolare la presentano molti composti essenziali per la vita: proteine, zuccheri, DNA. Una molecola di chiralità opposta a quella richiesta (ad esempio sinistra invece di destra) non può inserirsi nell'organismo: sebbene i due enantiomeri abbiano in linea di principio le stesse proprietà, negli organismi la Natura ha fatto una scelta che li rende differenti. Si discute anche della possibile causa di questa rottura di simmetria.
Asimmetrie: violazione della Parità e neutrino allo specchio tratta della scoperta della violazione della simmetria per trasformazione di "Parità" in un processo di Interazione Debole (vedete Interazione Debole ), con il neutrino come primo (invisibile) protagonista. Essendo soggetto solo a quest'interazione, il neutrino è particolarmente atto al suo studio e ha portato alla ribalta la totale violazione di Parità che lo caratterizza. Come detto precedentemente, la scoperta di un’asimmetria al livello fondamentale delle particelle elementari e delle loro interazioni fu fatto totalmente nuovo e sensazionale. Con la violazione della Parità, le Asimmetrie penetrano nel mondo delle particelle e si manifestano come un fenomeno naturale di carattere generale.
Asimmetrie: come fu scoperta la violazione della Parità descrive il famoso esperimento che portò alla scoperta della violazione della Parità nell’Interazione Debole.
Asimmetrie: CP, tempo e antimateria scomparsa parla di una piccola ma importantissima asimmetria nelle Interazioni Deboli, la cosiddetta "violazione di CP". Come detto sopra, si può supporre che la simmetria CPT sia conservata. La violazione di CP ha quindi come conseguenza un'asimmetria per inversione T a livello fondamentale, superando la visione galileiana. Inoltre essa implica un diverso comportamento di materia e antimateria e quindi incide sul mistero della scomparsa dell’antimateria dagli istanti iniziali dell’Universo a oggi e della praticamente totale asimmetria materia-antimateria che riscontriamo attualmente.
Rottura Spontanea della Simmetria inizia introducendone il concetto, per poi illustrarne qualitativamente il ruolo nel meccanismo teorico secondo cui la presenza del "bosone di Higgs" (vedete Il bosone di Higgs: una rivoluzione rispetto al comune pensare è necessaria affinché le particelle elementari e i mediatori delle loro interazioni acquisiscano una massa finita.
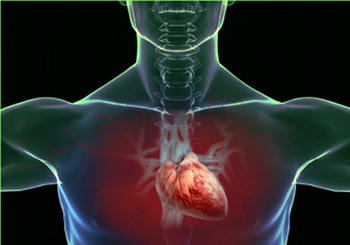
| .............................................................................................
Fig. 13. La collocazione asimmetrica del nostro cuore Immagine Imperial Bulldog | ..... | .................................................... In conclusione Accompagnando le Simmetrie, le Asimmetrie interessano praticamente tutti i campi della Scienza e ne costituiscono un tema unificante. La serie di articoli qui presentata intende far prendere coscienza di questo. Giungerete anche voi a concludere la facciata è dominata dalle Simmetrie, ma importantissimi aspetti sono governati dalle Antisimmetrie. Del resto, è così anche per il nostro corpo: esso è esternamente simmetrico, ma organi fondamentali non lo sono. Non lo è funzionalmente il cervello. Non lo è l’abilità delle nostre mani. E il solo cuore che abbiamo è situato a sinistra (figura 13). Se volessimo ragionare in termini di "peccato originale", il nostro cuore ci andrebbe di mezzo per primo. Non lo merita. |
Riferimenti bibliografici
La Fisica di Feynman (Simmetria nelle leggi fisiche, Vol 1, Cap. 52) regala sempre una lettura illuminante, in ogni tempo e stagione. Nella rivista Asimmetrie ( numero 11, 2011 ) potete trovare un insieme di articoli dedicati a Simmetrie e Asimmetrie nei loro diversi aspetti e attualità. Una rassegna approfondita è condotta da Franco Strocchi in Simmetrie e rotture di simmetrie in Fisica . Vi segnaliamo anche un articolo su Quantum Diaries : Symmetry in Physics, Part 2: Discrete Symmetries and Antimatter .
...
...
Gustavo Avitabile e Paolo Strolin
...
Ultima Modifica 8 Anni 11 Mesi fa da Paolo.
Si prega Accesso a partecipare alla conversazione.
Tempo creazione pagina: 0.584 secondi