Waves and particles for very curious pedestrians
- P. Strolin
-
Autore della discussione
- Offline
- Premium Utente
-
Less
Di più
12 Anni 6 Mesi fa - 10 Anni 9 Mesi fa #87
da P. Strolin
Birth of a new vision
The turn of the nineteenth century and the first decades of the twentieth century marked the beginning of a new era in Science as in other aspects of human culture. For example, in the visual arts the Impressionism gave way to modern art and all of its evolutions and revolutions.
In the first decades of the 20th century, “impossible” (according to the usual thinking at those times) experimental facts were elaborated by unbelievable intellectual activities and led to the “Wave-Quantum Mechanics”. It’s not limited to the macroscopic world as is the “Classic Mechanics”, which remains still valid in its domain.
In the same years the “Theory of Relativity” was conceived, a marvellous and fundamental intellectual construction stemming from the experimental fact that the speed of light is constant, independent of the reference system. Nothing is needed to justify the unicum of the velocity of light in Maxwell's equation.
Those were exceptional decades in the history of Science. The scientific and cultural revolution, which then occurred, has an extraordinary practical impact on our present lives. The Wave-Quantum Mechanics has pervaded our lives with its technological applications to electronics. Without the Relativity, the GPS navigator could not help you to find your way to that good pizzeria where you want to go: the GPS needs Relativity both the Special and the General one. For instance, if we would disregard the General Relativity, a GPS giving today your correct position would be wrong by 10 km tomorrow. Almost a century has gone after that revolution, which has had such important effects also in our daily life. Still, very strikingly, even among cultivated people only a small fraction understands its conceptual basis in terms of Physics.
We will see here the main points of the Wave-Quantum Mechanics, at a level understandable by people not equipped with professional mathematical tools: “Waves and particles for very curious pedestrians”, paraphrasing the title of Harry Lipkin’s book about “Group Theory” and adding “very curious”.
We will live the emotions of Science in connecting and sublimating experimental facts in theoretical syntheses. This implies already having scientific awareness of the basic facts, so that the text will not be burdened with frequent references.
New experimental facts
New theories are based on new experimental facts and/or careful interpretation of existing data. The new experimental facts that we are interested in are really intriguing. Electromagnetic waves, as light is, were experimentally proven to behave also like particles: think about the “photoelectric effect”. It was also seen that in certain circumstances the elementary particles have the behaviour of waves: they show "interference phenomena" typical of waves.
Among these experimental facts, we first recall the photoelectric effect. An electromagnetic radiation can transmit energy to electrons in an atom so as to extract them from the atom itself. According to the wave theory of the electromagnetic radiation, formulated by Maxwell shortly after mid-nineteenth century, it is expected that reducing the intensity of the radiation one may reach the point where it would not carry enough energy to extract electrons from the atom. It is not so! The phenomenon is attenuated but persists. It does not depend on the intensity but rather on the “frequency” of the wave.
The interpretation given by Einstein was that the energy comes in packets, called "quanta". This behaviour is typical of particles. Decreasing the intensity of the radiation, one only reduces the flow of quanta. The energy E of each quantum depends solely on the frequency f of the radiation through multiplication by a constant h, so that conceptually they are different ways to represent the same thing: E = h f. The constant is the "Planck's constant" h, which in this way enters boldly into the world of Physics characterizing the wave-quantum level. We enter a new domain of Science.
The Planck’s constant has a very low value: h = 1,2 x 10 -13 (GeV/c) cm. The related phenomena are thus invisible at a macroscopic level.
Experiments with slits
In classical physics, interference phenomena are typical of waves and experiments with slits offer an effective methodology to observe them. In this way Young’s experiment (1803) showed evidence of the wave behaviour of light. We will see the interference between waves that pass through a double slit. We will also see what happens with elementary particles.
The double slit methodology applied to waves and particles is beautifully described and interpreted in the precious “Feynman’s Physics” [R.P. Feynman, R.B. Leighton and M. Sands, The Feynman’s Lectures on Physics, Vol. 3, Cap. 1, Addison Wesley (1965). We will follow its approach. The two figures that follow are fully taken from Feynman’s Physics. In their schematic way, they represent so called "thought experiments", of conceptual nature but adhering to the experimental reality. This is a very effective method to understand physical phenomena.
We refer to these figures and not to others, maybe technically better, also as a tribute to Richard Feynman . You are invited to read Feynman’s Physics, his books of popular Science and everything he has written, not only on Physics topics. It is also recommend to listen on the Web an extraordinary lecture by Richard Feynman .
What happens with waves and particles on slits is shown by a nice animation . And why you should not listen a fancy lecture by Dr. Quantum ?
Waves on slits
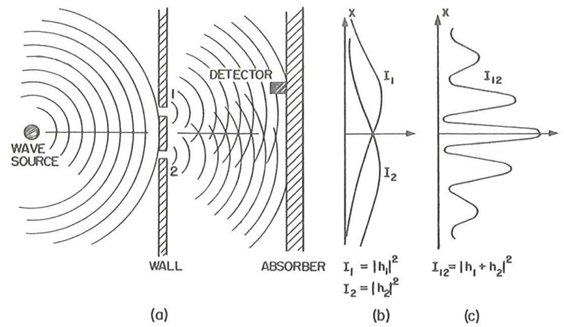
The first figure shows schematically what happens when waves (of any kind) invest two slits located at a distance comparable to the wavelength: on an observation plane over the slits, their intensity shows interference fringes (c) typical of waves. This already happens in Classical Physics. For electromagnetic waves (such as light), is this behaviour maintained when the intensity of the source is reduced indefinitely? At a certain point you start to see that the signal is not continuous. It comes in shots, for instance seen as individual spots of light on a monitor connected to the detector: you observe individual "quanta", thus confirming what the photoelectric effect tells. The quanta of electromagnetic radiation are called "photons". We have gone beyond Classical Physics: as in the photoelectric effect, electromagnetic waves are also particles!
But the story is even more incredible. Fascinated by what we are observing, we accumulate an increasing number of bright spots on the screen. We find that they tend to distribute themselves in bands separated by empty areas: the image that is being built resembles the classic interference fringes typical of waves! It looks as photons are capable of passing through "both" slits at the same time, and to interfere with themselves ....
Electrons on slits
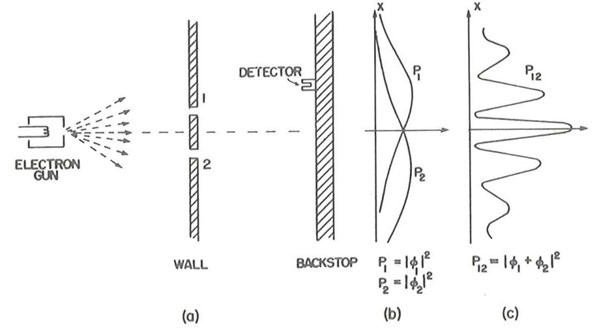
Let us now turn our attention to the second figure and consider that the slits are hit by elementary particles, such as electrons. Now let’s "imagine" to gradually decrease the width of the slits and their distance. Surprise: interference fringes appear, as shown (in a purely indicative way) in (c) of the figure! From the distance between the fringes one could be also infer which wavelength is associated to the electrons.
One would find that the wavelength λ, associated to particles (the so called "de Broglie" wavelength) is given by inverse of their momentum p multiplied by a constant, again the Planck constant h: λ= h / p ! Once more, we have gone beyond Classical Physics: particles are also waves!
In a real experiment the slits must have extremely small dimensions and distances: the reference variable is the de Broglie’s wavelength of the electron, which is linked to the tiny value of the Planck’s constant. However, using very sophisticated techniques the experiment was actually performed in 1976 at the University of Bologna and the quantum interference of single electrons was observed.
When particles are spied
Surprises add to surprises. Imagine being able, somehow, to determine which of the two slits the electron has passed through: the interference pattern disappears! If observed, electrons react like children do and become "well behaved particles". Their behaviour as waves is linked to the uncertainty in the slit through which they have gone. A new word breaks into the rigorous world of Physics: "uncertainty"!
Uncertainty and probability
This new and shocking word is materialized in Heisenberg’s "uncertainty principle", according to which we cannot determine with infinite precision two associated quantities such as position and momentum of a particle. The level of uncertainty is given by Planck's constant h. The word “probability” enters into the world of Physics. The absolute certainties of nineteenth century are abruptly changed in the probabilistic realities, as in other fields of life or of knowledge: Physics is humanized. The new phenomena are governed by the new fundamental constant of Physics, the Planck’s constant h.
Wave-Quantum Mechanics
In his lecture about the above experiments with two slits, Feynman says: “We choose to examine a phenomenon which is impossible, absolutely impossible, to explain in any classical way, and which has in it the heart of Quantum Mechanics. In reality, it contains the only mystery".
We can well realize the conceptual revolution which had occurred, hence the fascinating scientific challenge set by the intellectual need to frame in a consistent picture such amazing, crazy if you like, phenomena. "Quantum-Wave Mechanics" is indeed able to frame them in a consistent mathematical structure. Particles can be represented as waves, or more precisely as "wave packets" (the precise understanding of what this means requires some mathematics and is not necessary at this level). To electromagnetic waves is related a particle, the "photon" with mass strictly zero and then speed absolutely equal to the speed of light.
You might ask the question: how does Quantum-Wave Mechanics mathematically reconcile waves and particles? Don’t be surprised if I propose you go out for a short sail. The sea tends to become rough. The height (let’s say the amplitude) of the waves doubles, fortunately without that the waves break up. The fear quadruples (as the square of two), because it is connected to the physical quantity that characterizes the impact of the waves: the energy carried by them. Waves have ups and downs, the energy transmitted to the boat (the square of the amplitude) is always positive.
All waves are waves. In Quantum-Wave Mechanics, calculations are made in terms "probability amplitudes" (in the analogy, corresponding to the amplitude of sea waves), but the practical effects (such as the impact of the waves) are given by “probabilities” and these are connected to the square of the probability amplitudes. Notice that this ensures that probabilities are always positive. In a few concise words, the probability amplitudes imply a behaviour of waves and the behaviour of particles is described in terms of probabilities: waves and particles are included in the same magic framework, they are no longer totally different things. Sailing is a pleasure that helps us to understand Physics.
We do alwaya well to raise objections in order to understand. What said above might be applicable only to a special particle, the electron. Therefore, its validity may be confined to a very narrow niche, of interest only for specialists. The objection is doubly rejected. First of all, the electron is leading actor of phenomena and of electrical or elelctronic devices, which are integrated in our everyday life. In addition, wave-quantum mechanics has a general validity and is not restricted to the world of elementary particles. Recent experiments have shown that the wave-particle behaviour also applies to molecules, and even large ones. Look at the above expression of the wavelength as a function of momentum: you can well expect that in our macroscopic world (large momentum) the wavelengths of bodies are so small that no wave behaviour is detectable. Within its own domain, Classical Physics remains valid. No excuse not to study it!
We need it!
Finally here is the unavoidable, mandatory question: what’s for? If you do not believe that Wave-Quantum Mechanics is useful, be consistent and stop using electronic technologies pervading our daily life. Begin with that kind of prosthesis called mobile phone.
Thanks to "our friend" Crisostomo Sciacca for various suggestions and for having thus put further emphasis on the charm and mystery of wave-particle Physics.
.
.
.
Professore Emerito di Fisica Sperimentale
Università di Napoli "Federico II"
Complesso Univ. Monte S. Angelo
Via Cintia - 80126 Napoli - Italy
Waves and particles for very curious pedestrians è stato creato da P. Strolin
Waves and particles for very curious pedestrians
...................................................
................
For questions: author or
Ask an expert
................| ...................................................
Priest Baozhi (J. Hoshi)
Saio-ji Temple, Kyoto Heian Period (794-1185) | ..... | ................................................... L ook at the sculpture of Buddhist priest of the Heian Period (794-1185), which is now entrusted to the Kyoto National Museum . The image stems from a figurative art in which the symbolic value has a basic role. It’s not a direct representation of reality. It’s a magic wooden materialization of a mental image, linked to a philosophical vision. It strikes and attracts us with its subtle and deep mystery. Wouldn’t you like to decipher it? When we hear about the “ wave-particle dualism ”, we have similar feelings. But the mystery can be rationally investigated. We will see that the physical reality is absolutely beautiful and different from what the word “dualism” seems to mean. In classical physics waves and particles were considered as different physical entities, to be considered as alternatives. With modern physics it emerges, instead, a “holistic” picture, in which waves and particles are seen within a single global vision. It is like passing from a simple and rough distinction between men and women to a deeper view: in terms of Ying and Yang, present in different proportions but always within the same human circle. It’s well represented by the well-known symbol, which is not necessary to show again here. |
Birth of a new vision
The turn of the nineteenth century and the first decades of the twentieth century marked the beginning of a new era in Science as in other aspects of human culture. For example, in the visual arts the Impressionism gave way to modern art and all of its evolutions and revolutions.
In the first decades of the 20th century, “impossible” (according to the usual thinking at those times) experimental facts were elaborated by unbelievable intellectual activities and led to the “Wave-Quantum Mechanics”. It’s not limited to the macroscopic world as is the “Classic Mechanics”, which remains still valid in its domain.
In the same years the “Theory of Relativity” was conceived, a marvellous and fundamental intellectual construction stemming from the experimental fact that the speed of light is constant, independent of the reference system. Nothing is needed to justify the unicum of the velocity of light in Maxwell's equation.
Those were exceptional decades in the history of Science. The scientific and cultural revolution, which then occurred, has an extraordinary practical impact on our present lives. The Wave-Quantum Mechanics has pervaded our lives with its technological applications to electronics. Without the Relativity, the GPS navigator could not help you to find your way to that good pizzeria where you want to go: the GPS needs Relativity both the Special and the General one. For instance, if we would disregard the General Relativity, a GPS giving today your correct position would be wrong by 10 km tomorrow. Almost a century has gone after that revolution, which has had such important effects also in our daily life. Still, very strikingly, even among cultivated people only a small fraction understands its conceptual basis in terms of Physics.
We will see here the main points of the Wave-Quantum Mechanics, at a level understandable by people not equipped with professional mathematical tools: “Waves and particles for very curious pedestrians”, paraphrasing the title of Harry Lipkin’s book about “Group Theory” and adding “very curious”.
We will live the emotions of Science in connecting and sublimating experimental facts in theoretical syntheses. This implies already having scientific awareness of the basic facts, so that the text will not be burdened with frequent references.
New experimental facts
New theories are based on new experimental facts and/or careful interpretation of existing data. The new experimental facts that we are interested in are really intriguing. Electromagnetic waves, as light is, were experimentally proven to behave also like particles: think about the “photoelectric effect”. It was also seen that in certain circumstances the elementary particles have the behaviour of waves: they show "interference phenomena" typical of waves.
Among these experimental facts, we first recall the photoelectric effect. An electromagnetic radiation can transmit energy to electrons in an atom so as to extract them from the atom itself. According to the wave theory of the electromagnetic radiation, formulated by Maxwell shortly after mid-nineteenth century, it is expected that reducing the intensity of the radiation one may reach the point where it would not carry enough energy to extract electrons from the atom. It is not so! The phenomenon is attenuated but persists. It does not depend on the intensity but rather on the “frequency” of the wave.
The interpretation given by Einstein was that the energy comes in packets, called "quanta". This behaviour is typical of particles. Decreasing the intensity of the radiation, one only reduces the flow of quanta. The energy E of each quantum depends solely on the frequency f of the radiation through multiplication by a constant h, so that conceptually they are different ways to represent the same thing: E = h f. The constant is the "Planck's constant" h, which in this way enters boldly into the world of Physics characterizing the wave-quantum level. We enter a new domain of Science.
The Planck’s constant has a very low value: h = 1,2 x 10 -13 (GeV/c) cm. The related phenomena are thus invisible at a macroscopic level.
Experiments with slits
In classical physics, interference phenomena are typical of waves and experiments with slits offer an effective methodology to observe them. In this way Young’s experiment (1803) showed evidence of the wave behaviour of light. We will see the interference between waves that pass through a double slit. We will also see what happens with elementary particles.
The double slit methodology applied to waves and particles is beautifully described and interpreted in the precious “Feynman’s Physics” [R.P. Feynman, R.B. Leighton and M. Sands, The Feynman’s Lectures on Physics, Vol. 3, Cap. 1, Addison Wesley (1965). We will follow its approach. The two figures that follow are fully taken from Feynman’s Physics. In their schematic way, they represent so called "thought experiments", of conceptual nature but adhering to the experimental reality. This is a very effective method to understand physical phenomena.
We refer to these figures and not to others, maybe technically better, also as a tribute to Richard Feynman . You are invited to read Feynman’s Physics, his books of popular Science and everything he has written, not only on Physics topics. It is also recommend to listen on the Web an extraordinary lecture by Richard Feynman .
What happens with waves and particles on slits is shown by a nice animation . And why you should not listen a fancy lecture by Dr. Quantum ?
Waves on slits (from Feynman's Physics)
Waves on slits
The first figure shows schematically what happens when waves (of any kind) invest two slits located at a distance comparable to the wavelength: on an observation plane over the slits, their intensity shows interference fringes (c) typical of waves. This already happens in Classical Physics. For electromagnetic waves (such as light), is this behaviour maintained when the intensity of the source is reduced indefinitely? At a certain point you start to see that the signal is not continuous. It comes in shots, for instance seen as individual spots of light on a monitor connected to the detector: you observe individual "quanta", thus confirming what the photoelectric effect tells. The quanta of electromagnetic radiation are called "photons". We have gone beyond Classical Physics: as in the photoelectric effect, electromagnetic waves are also particles!
But the story is even more incredible. Fascinated by what we are observing, we accumulate an increasing number of bright spots on the screen. We find that they tend to distribute themselves in bands separated by empty areas: the image that is being built resembles the classic interference fringes typical of waves! It looks as photons are capable of passing through "both" slits at the same time, and to interfere with themselves ....
Electrons on slits (from Feynman's Physics)
Electrons on slits
Let us now turn our attention to the second figure and consider that the slits are hit by elementary particles, such as electrons. Now let’s "imagine" to gradually decrease the width of the slits and their distance. Surprise: interference fringes appear, as shown (in a purely indicative way) in (c) of the figure! From the distance between the fringes one could be also infer which wavelength is associated to the electrons.
One would find that the wavelength λ, associated to particles (the so called "de Broglie" wavelength) is given by inverse of their momentum p multiplied by a constant, again the Planck constant h: λ= h / p ! Once more, we have gone beyond Classical Physics: particles are also waves!
| .........................................................
http://www.scienzaescuola.eu/images/articoli/onde3.jgif
Animation of elettrons on slits (da
Wikipedia)
| ..... | .................................. We said "imagine" and so we took advantage of the educational benefits of the methodology of "thought experiments". Continuing with the imagination, the animation on the leftt shows how the representations of electrons as waves or particles can conceptually co-exist. In an experiment able to see both the impact of single electrons and the interference fringes, one would see the individual electrons accumulate and distribute themselves according to the interference fringes. But performing such an experiment is very difficult. |
In a real experiment the slits must have extremely small dimensions and distances: the reference variable is the de Broglie’s wavelength of the electron, which is linked to the tiny value of the Planck’s constant. However, using very sophisticated techniques the experiment was actually performed in 1976 at the University of Bologna and the quantum interference of single electrons was observed.
When particles are spied
Surprises add to surprises. Imagine being able, somehow, to determine which of the two slits the electron has passed through: the interference pattern disappears! If observed, electrons react like children do and become "well behaved particles". Their behaviour as waves is linked to the uncertainty in the slit through which they have gone. A new word breaks into the rigorous world of Physics: "uncertainty"!
Uncertainty and probability
This new and shocking word is materialized in Heisenberg’s "uncertainty principle", according to which we cannot determine with infinite precision two associated quantities such as position and momentum of a particle. The level of uncertainty is given by Planck's constant h. The word “probability” enters into the world of Physics. The absolute certainties of nineteenth century are abruptly changed in the probabilistic realities, as in other fields of life or of knowledge: Physics is humanized. The new phenomena are governed by the new fundamental constant of Physics, the Planck’s constant h.
Wave-Quantum Mechanics
In his lecture about the above experiments with two slits, Feynman says: “We choose to examine a phenomenon which is impossible, absolutely impossible, to explain in any classical way, and which has in it the heart of Quantum Mechanics. In reality, it contains the only mystery".
We can well realize the conceptual revolution which had occurred, hence the fascinating scientific challenge set by the intellectual need to frame in a consistent picture such amazing, crazy if you like, phenomena. "Quantum-Wave Mechanics" is indeed able to frame them in a consistent mathematical structure. Particles can be represented as waves, or more precisely as "wave packets" (the precise understanding of what this means requires some mathematics and is not necessary at this level). To electromagnetic waves is related a particle, the "photon" with mass strictly zero and then speed absolutely equal to the speed of light.
You might ask the question: how does Quantum-Wave Mechanics mathematically reconcile waves and particles? Don’t be surprised if I propose you go out for a short sail. The sea tends to become rough. The height (let’s say the amplitude) of the waves doubles, fortunately without that the waves break up. The fear quadruples (as the square of two), because it is connected to the physical quantity that characterizes the impact of the waves: the energy carried by them. Waves have ups and downs, the energy transmitted to the boat (the square of the amplitude) is always positive.
All waves are waves. In Quantum-Wave Mechanics, calculations are made in terms "probability amplitudes" (in the analogy, corresponding to the amplitude of sea waves), but the practical effects (such as the impact of the waves) are given by “probabilities” and these are connected to the square of the probability amplitudes. Notice that this ensures that probabilities are always positive. In a few concise words, the probability amplitudes imply a behaviour of waves and the behaviour of particles is described in terms of probabilities: waves and particles are included in the same magic framework, they are no longer totally different things. Sailing is a pleasure that helps us to understand Physics.
We do alwaya well to raise objections in order to understand. What said above might be applicable only to a special particle, the electron. Therefore, its validity may be confined to a very narrow niche, of interest only for specialists. The objection is doubly rejected. First of all, the electron is leading actor of phenomena and of electrical or elelctronic devices, which are integrated in our everyday life. In addition, wave-quantum mechanics has a general validity and is not restricted to the world of elementary particles. Recent experiments have shown that the wave-particle behaviour also applies to molecules, and even large ones. Look at the above expression of the wavelength as a function of momentum: you can well expect that in our macroscopic world (large momentum) the wavelengths of bodies are so small that no wave behaviour is detectable. Within its own domain, Classical Physics remains valid. No excuse not to study it!
We need it!
Finally here is the unavoidable, mandatory question: what’s for? If you do not believe that Wave-Quantum Mechanics is useful, be consistent and stop using electronic technologies pervading our daily life. Begin with that kind of prosthesis called mobile phone.
Thanks to "our friend" Crisostomo Sciacca for various suggestions and for having thus put further emphasis on the charm and mystery of wave-particle Physics.
Paolo Strolin
(translated together with Roberto Albarella)
(translated together with Roberto Albarella)
.
.
.
Professore Emerito di Fisica Sperimentale
Università di Napoli "Federico II"
Complesso Univ. Monte S. Angelo
Via Cintia - 80126 Napoli - Italy
Ultima Modifica 10 Anni 9 Mesi fa da .
Si prega Accesso a partecipare alla conversazione.
Tempo creazione pagina: 0.495 secondi